Информационные технологии.
Задача 1.
Проводится проверка гипотезы о равенстве цен на товар в двух регионах.
Получены следующие данные:
-
Variable
Mean
Std.Dv
P-level
X15
12,1
1,22
X16
25,0
15,54
0,104
Можно ли считать, что средние значения цен в двух регионах равны при заданной доверительной вероятности 0,85. Ответ объяснить.
Решение.
Так как P-level=0,104<0,15 гипотезу о равенстве средних значений цен следует отвергнуть.
Задача 2.
Проводится проверка гипотезы о равенстве среднего дохода населения в двух регионах. Получены следующие данные:
-
Variable
Mean
Std.Dv
P-level
X1
1687
107.9146
X2
1620
248.5514
0,319316
Можно ли считать что средние доходы населения в двух регионах равны при заданной доверительной вероятности 0,8. Ответ объяснить.
Решение.
Так как P-level=0,319316>0,2, то гипотезу о равенстве средних доходов населения в двух регионах следует принять.
Задача 3.
Имеются следующие результаты расчётов параметров регрессионной модели:
-
BETA
St.Err of BETA
B
St.Err of B
P-level
Intercept
3401.0
153.0
0.00000
1/V1
-1.000
0.25725
-2781000
7115.72
0.00000
LN(V3)
0.27
0.25725
-8.0
16.72
0.04711
Какой вид имеет уравнение регрессии?
Решение.
У=3401-2781000/V1 - 8*LN(V3)
Задача 4.
Имеются следующие результаты расчётов параметров регрессионной модели:
-
BETA
St.Err of BETA
B
St.Err of B
P-level
Intercept
23.638
2.07
0.0003
Х**5
0.979
0.101
1.036
1.07
0.0006
Какой вид имеет уравнение регрессии?
Решение.
У=1,036*Х5+23,638
Задача 5.
Реляционная модель базы данных имеет следующий вид:
Товарная продукция (Вид продукции, Цена, Себестоимость, Объем продаж).
Написать SQL-запрос, позволяющий рассчитать прибыль от реализации каждого вида продукции.
Решение.
Select [Вид продукции],(Цена-Себестоимость)*[Объем продаж]AS[Прибыль от реализации]FROM[Товарная продукция]
Задача 6.
Реляционная модель базы данных имеет следующий вид:
Товарная продукция (Вид продукции, Цена, Себестоимость, Объем продаж).
Написать SQL-запрос, позволяющий рассчитать рентабельность продукции каждого вида.
Решение.
Select [Вид продукции],(Цена-Себестоимость)/СебестоимостьAS[Рентабельность продукции]FROM[Товарная продукция]
Задача 7.
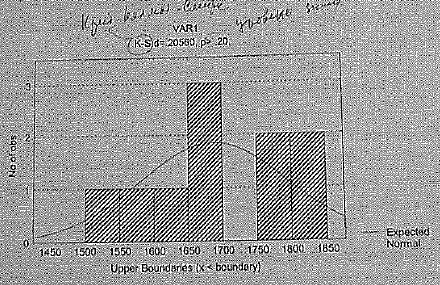
Определить, подчиняется ли случайная величина нормальному закону распределения при заданной вероятности 0,9
Решение.
Так как расчётное значение P>0,2, то при заданной вероятности 0,9 и при уровне значимости 1-0,9=0,1, гипотезу о нормальном законе распределения следует принять.
Задача 8.
Является ли временной ряд стационарным? Ответ объяснить.
Решение.
Так как коэффициенты автокорреляции близки к нулю, ряд является стационарным.
Задача 9.
Имеются следующие данные об ошибках прогноза при экспоненциальном сглаживании:
-
Mean error
0.095
Mean absolute error
0.837
Sum of squares
8.088
Mean square
1.01
Mean percentage error
-1.063
Mean absolute percentage error
15.500
Можно ли использовать для прогнозирования эту модель? Что можно сказать о точности прогноза? Ответ объяснить.
Решение.
Модель можно использовать, так как MPE<5%. Точность прогноза хороша, т.к. MAPE<20%
Задача 10.
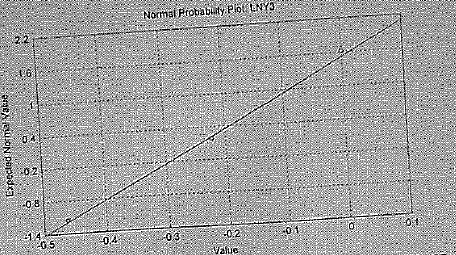
Можно ли считать распределение случайной величины нормальным? Ответ объяснить.
Решение.
Да, так как все точки на графике близки к диагонали.
Задача 11.
Имеются следующие результаты расчётов параметров регрессионной модели.
-
BETA
St.Err of BETA
B
St.Err of B
P-level
Intercept
7,7
6,29
0,0345
VAR1
0,75
0,105
0,05
0,006
0,0470
VAR2
0,64
0,096
0,32
0,04
0,5233
VAR3
0,68
0,131
5,3
1,03
0,0362
Определить, какие переменные следует включить в модель. Ответ объяснить.
Решение.
В модель следует включить переменные, у которых P-level<0,05 то есть переменные VAR1 и VAR3
Задача 12.
Имеются следующие результаты расчётов параметров регрессионной модели.
-
BETA
St.Err of BETA
B
St.Err of B
P-level
Intercept
200,82
23,362
0,023
VAR1
0,62
0,320
-54,26
5,315
0,043
VAR2
0,52
0,103
8,64
6,286
0,001
VAR3
0,86
0,145
15,36
1,033
0,062
VAR4
0,90
0,050
-30,12
8,862
0,012
Определить, какие переменные следует включить в модель. Ответ объяснить.
Решение.
В модель следует включить переменные, у которых P-level<0,05 то есть переменные VAR1 VAR2 и VAR4
Задача 13.
Для одного и того же массива данных выполнены расчеты по двум моделям:
Модель 1.
-
BETA
St.Err of BETA
B
St.Err of B
P-level
Intercept
185,531
224,120
0,454
VAR1
0,408
0,456
7,430
8,324
0,423
Модель 2.
-
BETA
St.Err of BETA
B
St.Err of B
P-level
VAR1
0,991
0,065
13,957
2,548
0,0029
Какую модель следует выбрать? Какой вид имеет уравнение регрессии для выбранной модели?
Решение.
Так как P-level<0,05 в модели 2, выбранное уравнение регрессии имеет вид :
У=13,957* VAR1
Задача 14.
Имеются следующие результаты расчетов параметров регрессионной модели:
-
BETA
St.Err of BETA
B
St.Err of B
P-level
Intercept
12,389
1,03
0,0027
Х**2
0,991
0,065
0,018
0,01
0,00011
Какой вид имеет уравнение регрессии?
Решение.
У=0,018*Х2+12,389
Задача 15.
Имеются следующие результаты расчетов параметров регрессионной модели:
-
BETA
St.Err of BETA
B
St.Err of B
P-level
Intercept
23,638
2,07
0,0003
SQR-X
0,979
0,101
1,036
1,07
0,0006
Какой вид имеет уравнение регрессионной модели?
Решение.
У=1,036*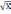
+23,638
Задача 16.
Имеются следующие результаты расчётов параметров регрессионной модели.
-
BETA
St.Err of BETA
B
St.Err of B
P-level
Intercept
7,70
6,28
0,0345
VAR1
0,75
0,15
0,05
0,006
0,0470
VAR2
0,64
0,36
0,32
0,04
0,0423
VAR3
0,68
0,34
-5,31
1,03
0,0362
Какой вид имеет уравнение регрессии?
Решение.
У=7,70+0,05* VAR1+0,32* VAR2-5,31* VAR3
Задача 17.
Имеются следующие данные об ошибках прогноза при экспоненциальном сглаживании:
-
Mean error
-1,963
Mean absolute error
2,674
Sum of squares
145,156
Mean square
10,368
Mean percentage error
-27,999
Mean absolute percentage error
32,961
Можно ли использовать для прогнозирования эту модель? Что можно сказать о точности прогноза? Ответ объяснить.
Решение.
Модель
можно использовать, так как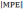 
=27,999>5%.
точность прогноза следует считать
неудовлетворительной, такую модель
использовать нельзя.
Задача 18.
-
Номер модели
Alpha
Mean Error
Mean Abs Error
Sums of Squares
Mean Squares
Mean % Error
Mean Abs % Error
1
0,1
-0,88735
24,45301
19204,24
1600,353
-9,84688
21,6203
2
0,2
-1,83242
26,32302
20497,84
1708,153
-11,0994
23,71243
3
0,3
-2,39138
27,46796
21491,03
1790,919
-11,7719
25,03969
4
0,4
-2,55478
27,71656
22320,12
1860,01
-11,8868
25,4069
5
0,5
-2,45338
27,40177
23117,68
1926,473
-11,6047
25,11176
6
0,6
-2,22704
27,93201
23969,55
1997,463
-11,088
25,51011
7
0,7
-1,97776
29,21865
24922,67
2076, 889
-10,4522
26,51442
8
0,8
-1,76176
30,2046
26004,12
2167,01
-9,75967
27,09788
Какую модель следует выбрать для прогнозирования. Ответ объяснить. Какой вид имеет уравнение в выбранной модели?
Решение.
Модель
№1, имеющая минимальные ошибки. 
С2
С1
Свойство
О2
О1
Ответ
Задача 19.
Какой вид имеет соответствующая реляционная модель?
Решение.
R1(O1,C1) R2(O2,C2) R3(O1,O2)
Задача 20.
О1
О2
С1
Какой вид имеет соответствующая реляционная модель?
Решение.
R1(O1,O2,C1)
Финансовый менеджмент
Математический метод
Логистика. Запасы.
Задача 1
Годовая потребность в материалах 500т.
Число рабочих дней в году 226.
Время поставки 6 дней.
Возможная задержка 1 день.
Определить max потребления за время поставки в системе с фиксированным размером заказа если известно, что ожидаемая потребность за время поставки 2 тонны.
Решение
Максимальное потребление за время поставки = (Время поставки + Задержка поставки)* расход=(6+1)*2=14т.
Задача 2
Определить в системе с фиксированным размером заказа гарант. заказ, если известно, что ожидаемое потребление составляет 80 тонн.
Максим. потребление за время поставки 100 тонн.
Решение
100-80=20т.
Задача 3
Рассчитать ожидаемое потребление за время поставки в системе управления запасами с фиксированным интервалом времени между заказами, если ожидаемое дневное потребление 100т/день, а время поставки 10 дней.
Решение
100*10=1000т.
Задача 4
В системе управления запасами с фиксир. интервалами времени между заказами определить интервал времени между заказами, если годовое потребление составляет 5000т. Число рабочих дней 226.
Оптимальный размер заказа 350 т.
Решение
Интервал
времени =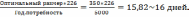 
Задача 5
В системе управления запасами с фиксированным интервалом времени определить максимально желательный запас, если интервал между заказом 11 дней.
Дневное потребление 5 тонн/день.
Гарантийный запас 10 тонн.
Решение
Макс = Гарант+ (интервал+ожидаемое дневное потребление)= 10+(11*5)=65 тонн
Задача 6
Определить долю дополнительных затрат, возникающих при доставке товара из Юго-Вост. Азии.
Решение
Транспортный тариф Т 105 долл./км.
Импортная пошлина Пи 10%
Ставка на запасы в пути Зп 1,7%
Страховые запасы Зс 0,6%
Стоимость товара в Европе ( не пригод) С 108 долл.
в Юго-Вост. Азии С 80 долл.
Удельная стоимость поставки груза У 2000долл./км.
Решение
Доля
дополнительных затрат Д=
%
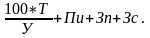Д=