Финансы и кредит

Задача № 1

Определить величину денежных агрегатов М₀, М₁, М₂, М₃ на основании следующих данных (в млн. ден. ед.):

- наличные денежные средства в банках 500

- срочные вклады населения в Сберегательном банке 1630

- депозитные сертификаты 645

- расчётные, текущие счета юридических лиц 448

- вклады населения до востребования 300

- наличные денежные средства в обращении 170.

Решение:

М₀ = наличные денежные средства в обращении;

М₁= М₀+расчётные и текущие счета юридических лиц+вклады населения до востребования;

М₂=М₁+срочные вклады населения в сберегательном банке;

М₃= М₂+депозитные сертификаты и облигации госзайма.

Ответ: М₀=170, М₁=918, М₂=2548, М₃=3193 млн. ден. ед.

Задача № 2

Дефлятор ВНП составляет 3,6. Номинальный ВНП 4 трлн. руб. Определить реальный ВНП.

Решение:

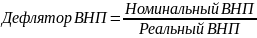
Ответ: 1,11 трлн. руб.

Задача № 3

Первоначальная сумма Р = 7000 руб. помещена в банк на срок n = 2 года под процентную ставку i = 15% годовых. Определить будущую сумму, при условии, что начисление процентов осуществляется по схеме простых процентов.

Решение:

FV=P*(1+n*i)

Ответ: 9100 руб.

Задача № 4

Первоначальная сумма Р = 6000 руб., наращенная сумма S = 7200 руб., процентная ставка i = 10% годовых (проценты простые). Определить период начисления процентов (n).

Решение:

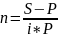
Ответ: 2 года

Задача № 5

Наращенная сумма S = 20000 руб., период начисления процентов n = 1,5 года, простая процентная ставка i = 17% годовых. Определить первоначальную сумму (P).

Решение:

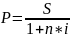
Ответ: 15936,25 руб.

Задача № 6

Первоначальная сумма Р = 24000 руб. В первой половине года применялась простая процентная ставка i₁ = 12% годовых, во второй половине года применялась простая процентная ставка i₂ = 15% годовых. Определить наращенную сумму (S).

Решение:

)

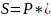S=P*(1+n₁*i₁+n₂*i₂)

Ответ: 27240 руб.

Задача № 7

Кредит на сумму 15000 руб. выдаётся на полгода по простой учётной ставке 12% годовых. Определить, какую сумму получит заёмщик.

Решение:

P=S*(1-n*d)

Ответ: 14100 руб.

Задача № 8

Вексель на сумму 35000 руб. с датой погашения 27 ноября 2010 года был учтён банком 11 августа 2010 года по простой учётной ставке 13% годовых. Продолжительность года составляет 365 дней. Определить, какая сумма была выплачена банком.

Решение:

P=S*(1- ).

t= 21(август)+30 (сентябрь)+31 (октябрь)+27 (ноябрь) -1=108 дней

Р=35000*(1-0,13*108/365)=33653,70

Ответ: 33653,70 руб.

Задача № 9

Первоначальная сумма Р = 37000 руб. помещена в банк на срок n = 2 года под i = 15% годовых (проценты сложные). Определить наращенную сумму.

Решение:

S=P*(1+i)ⁿ

Ответ: 48932,5 руб.

Задача № 10

Наращенная сумма S = 41000 руб., период начисления процентов составляет 2 года, сложная процентная ставка = 15% годовых. Определить первоначальную сумму.

Решение:

Р =

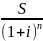
Ответ: 31001,89 руб.

Задача № 11

Первоначальная сумма P = 24000 руб., период начисления процентов составил 5 лет, причём в первые три года применялась сложная процентная ставка равная 12% годовых, а в оставшиеся два года применялась сложная процентная ставка равная 15% годовых. Определить наращенную сумму.

Решение:

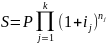
S=P*(1+i₁)ⁿ₁*(1+i₂)ⁿ₂

Ответ: 65458,27 руб.

Задача № 12

Первоначальная сумма составляет 14000 руб., период начисления процентов равен двум годам, сложная номинальная процентная ставка составляет 12% годовых. Проценты начисляются ежеквартально. Определить наращенную сумму.

Решение:

Ответ: 17734,78 руб.

Задача № 13

Первоначальная сумма P = 7000 руб., период начисления n = 4 года, сложная учётная ставка составляет 13% годовых. Определить наращенную сумму.

Решение:

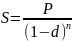
Ответ: 12218,59 руб.

Задача № 14

Каждый месяц цены растут на 2%. Определить, каков ожидаемый индекс инфляции за год.

Решение:

Индекс инфляции (I_и^год) = (1+рост цены)ⁿ, где n = 12 мес.

Ответ: т.е. цены за год вырастут в 1,27 раза или на 27%

Задача № 15

Уровень инфляции в марте составил 3%, в апреле – 5%, в мае – 3%. Определить индекс инфляции за рассматриваемый период.

Решение: I_и^год=(1+α_март)*(1+α_апрель)*(1+α_май)

Ответ: 11,4%

Задача № 16

Период начисления (n) составляет 6 месяцев (0,5 года), ожидаемый ежемесячный уровень инфляции 1,5%. Под какую простую ставку ссудных процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность i = 6% годовых (проценты простые).

Решение:

I_и^год = (1+ α)ⁿ =(1+0,015)⁶ = 1,0934, т.е. уровень инфляции (α) за рассматриваемый период составил 0,0934, тогда

Ставка ссудных процентов = 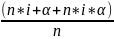= = 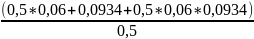0,2524, т.е. 25,24% годовых

Ответ: 25,24% годовых.

Задача № 17

Первоначальная сумма положена в банк на срок январь-июнь под простую ставку ссудных процентов i_α=25% годовых. Уровень инфляции в январе составил 0,5%, в феврале – 2%, в марте – 1%, в апреле – 0,5%, в мае – 3%, в июне – 1%. Определить, какова реальная доходность в виде годовой простой ставки ссудных процентов.

Решение:

n = 6 месяцев = 0,5 года.

I_и^год =(1+0,005)*(1+0,02)*(1+0,01)*(1+0,005)*(1+0,03)*(1+0,01)=1,0825, т.е. уровень инфляции за рассматриваемый период α =0,0825. Тогда реальная доходность в виде годовой простой ставки ссудных процентов

i =

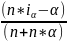
Ответ: 7,9% годовых.

Задача №18

Период начисления составляет 2 года, ожидаемый ежегодный уровень инфляции 12%. Определить, под какую ставку ссудных процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность i = 6% годовых (проценты сложные).

Решение:

I_и=(1+i_α)ⁿ =(1+0,12)²=1,2544, т.е. α=0,2544

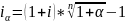=(1+0,06)* 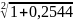- 1=0,1872

Ответ: 0,1872 или 18,72% годовых.

Задача № 19

Первоначальная сумма внесена на счёт в банке на срок 2 года под сложную ставку ссудных процентов i_α = 15% годовых. Уровень инфляции за первый год составил 12%, за второй год – 14%. Определить, какова реальная доходность в виде сложной годовой ставки ссудных процентов.

Решение:

I_и = (1+0,12)*(1+0,14)=1,2768, т.е. уровень инфляции α за рассматриваемый период составил 0,2768. Следовательно, реальная доходность в виде сложной годовой процентной ставки ссудных процентов будет равна:

i= 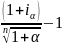= 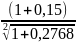- 1=0,0177 или 1,77% годовых.

Ответ: 1,77% годовых.

Задача № 20

Определить, какой вариант инвестирования первоначальной суммы на срок 0,5 года лучше: под простую процентную ставку 18% годовых или под простую учётную ставку 16% годовых.

Решение:

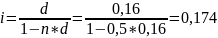(или 17,4% годовых), т.к. 17,4% ˂18%, то лучше вариант с постой процентной ставкой.

Ответ: лучше вариант с простой процентной ставкой.

Задача № 21

Определить, какой вариант инвестирования первоначальной суммы на срок 2 года лучше: под простую процентную ставку 17% годовых или под сложную процентную ставку 15,5% годовых.

Решение:

i=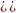 =((1+0,155)²-1)/2= 0,167 или 16,7% годовых, т.к. 16,7%˂17%, то лучше вариант с простой процентной ставкой.

Ответ: лучше вариант с простой процентной ставкой.

Задача № 22

Определить, какой вариант инвестирования первоначальной суммы на срок 2 года лучше: под простую процентную ставку 19% годовых или под номинальную сложную процентную ставку 14% годовых с ежемесячным начислением.

Решение:

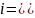=((1+0,14/12)^2*12-1)/2=0,1605 или 16,5% годовых, т.к. 16,5%˂19%, то лучше вариант с простой процентной ставкой.

Ответ: лучше вариант с простой процентной ставкой.

Задача № 23

Найти эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке 12% годовых с ежемесячным начислением.

Решение:

¹²-1=0,1268 или 12,68% годовых

Ответ: 12,68% годовых

Задача № 24

Найти годовую номинальную сложную процентную ставку (проценты начисляются каждые полгода), эквивалентную сложной процентной ставке 20% годовых.

Решение:

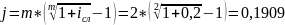, т.е. 19,09% годовых.

Ответ: 19,09% годовых

Задача № 25

Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Найти будущую сумму ренты постнумерандо.

Решение:

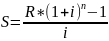= 4127,52 руб.

Ответ: 4127,52 руб.

Задача № 26

Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Найти будущую сумму ренты пренумерандо.

Решение:

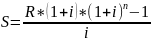= 4705,37 руб.

Ответ: 4705,37 руб.

Задача № 27

Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Определить современную стоимость простой ренты постнумерандо.

Решение:

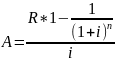= 2785,96 руб.

Ответ: 2785,96 руб.

Задача № 28

Определить размер ежегодных платежей в конце года по сложной процентной ставке 14% годовых для накопления через 4 года суммы 70000 руб. (простая рента постнумерандо).

Решение:

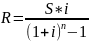=14224,33 руб.

Ответ: 14224,33 руб.

Задача № 29

Определить размер ежегодных платежей в начале года по сложной процентной ставке 14% годовых для накопления через 4 года суммы 70000 руб. (простая рента пренумерандо).

Решение:

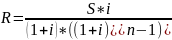=12477,49 руб.

Ответ: 12477,49 руб.

Задача № 30

Взят кредит на сумму 60000 руб. сроком на 4 года под 15% годовых. Определить размер ежегодных погасительных платежей в конце года.

Решение:

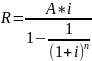= 21015,92 руб.

Ответ: 21015,92 руб.

Задача № 31

Взят кредит на сумму 60000 руб. сроком на 4 года под 15% годовых. Определить размер ежегодных погасительных платежей в начале года.

Решение:

= 18274,71 руб.

Ответ: 18274,71руб.

Задача № 32

Найти наращенную сумму общей ренты сроком (n) 2 года с выплатами (W) по 7000 руб. в конце каждого квартала (p) и начислением процентов по ставке (i) 11% годовых ежемесячно (m).

Решение:

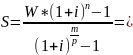7000*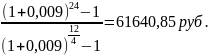

Ответ: 61640,85 руб.

Задача № 33

Выдан кредит на сумму 50000 руб. на 3 года по ставке 16% годовых ежеквартально. Определить размер полугодовых платежей.

Решение:

Здесь р = 2, m = 4, i = 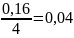, n = 3*m = 3*4 = 12.

=

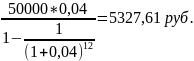
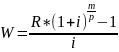=5327,61* 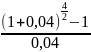=10868,32 руб.

Ответ: 10868,32 руб.

Задача № 34

Найти современную стоимость общей бессрочной ренты с выплатами по 9000 руб. в начале каждого полугодия и процентной ставкой 12% годовых ежеквартально.

Решение:

Здесь р = 2, m = 4, i = .

=

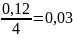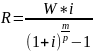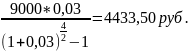
Тогда А=

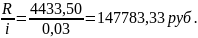
Ответ: 147783,33 руб.

Задача № 35

10 августа заёмщик обратился за получением ломбардного кредита и предоставил в залог ценности на сумму 90000 руб. Сумма ломбардного кредита составила 75% от стоимости залога, процентная ставка 14% годовых. Определить величину кредита.

Решение:

Ломбардный кредит обычно выдаётся на 3 месяца, используется французская практика (продолжительность года К=360 дней, учитывается точное количество дней в месяце). Следовательно, кредит предоставлен на 3 месяца (10 августа – 10 ноября), его срок составляет t = 22 дня (август) + 30 дней (сентябрь) + 31 день (октябрь) + 10 дней (ноябрь) – 1= 92 дня.

Определяем сумму ломбардного кредита Р = 90000 руб.*0,75 =67500 руб.

Далее определяем проценты I =

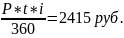
Заёмщик получит сумму в размере = 67500 – 2415 = 65085 руб.

Ответ: 65085 руб.

Задача № 36

Заёмщик должен одному кредитору следующие суммы P₁ = 7000 руб. (срок погашения 17 июля, процентная ставка i₁=9% годовых), Р₂=9000 руб. (срок погашения 23 августа, процентная ставка i₂ = 10% годовых), Р₃ = 10000 руб. (срок погашения 14 сентября, процентная ставка i₃= 12% годовых). Определить когда лучше выплатить весь долг сразу (процентная ставка i_s=11% годовых), чтобы при этом не понесли ущерба ни кредитор, ни заёмщик.

Решение:

Примем дату первого погашения – 17 июля – за нулевой момент времени. Тогда t₁=0, t₂ (17 июля – 23 августа) = 38 дней, t₃ (17 июля – 14 сентября) = 60 дней.

Средний срок погашения ссуды (t_s) = =

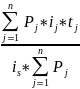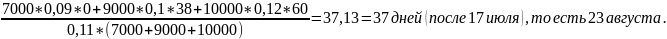
Ответ: 23 августа.

Задача № 37

Схема налога на проценты: 3% с части дохода от 0 до 5000 руб.; 5% с части дохода от 5000 до 15000 руб.; 8% с части дохода от 15000 до 30000 руб.; 12% с части дохода от 30000 до 50000 руб. и 20% с части дохода свыше 50000 руб. Начислены проценты в размере 56000 руб. Найти среднюю и предельную ставки налога.

Решение:

Разобьём сумма начисленных процентов (56 000 руб.) на части, соответствующие предельным ставкам налога: 56000 = 5000+10000+15000+20000+6000. С каждой части удерживаем соответствующий налог: 5000*0,03+10000*0,05+15000*0,08+20000*0,12+6000*0,2=5450 руб.

Средняя ставка налога 5450/56000*100%=9,73%.

Так как величина начисленных процентов составляет 56000 руб., то предельная ставка налога будет равна 20%.

Ответ: средняя ставка составляет 9,73%; предельная ставка налога 20%.

Задача № 38

Первоначальная сумма составляет 7000 руб., период начисления 0,25 года, простая процентная ставка – 14% годовых, ставка налога на проценты – 12%. Определить наращенную сумму.

Решение:

S=P*(1+i*n*(1-q)) = 7000*(1+0,14*0,25*(1-0,12))=7215,6 руб.

Ответ: 7215,6 руб.

Задача № 39

Первоначальная сумма составляет 7000 руб. период начисления 0,5 года, простая учётная ставка 15% годовых, ставка налога на проценты 11%. Найти наращенную сумму.

Решение:

=

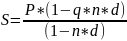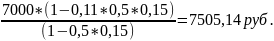
Ответ: 7505,14 руб.

Задача № 40

Первоначальная сумма составляет 12000 руб., период начисления 2 года, сложная процентная ставка 14% годовых, ставка налога на проценты 10%. Найти наращенную сумму.

Решение:

S=P*((1-q)*(1+i)ⁿ+q) = 12000*((1-0,1)*(1+0,14)²+0,1)=15235,68 руб.

Ответ: 15235,68 руб.

Задача № 41

При выдаче кредита на 0,25 года по простой процентной ставке 14% годовых удерживаются комиссионные (h) в размере 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки простых процентов (i_э).

Решение:

i_э= 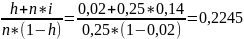, т.е. 22,45% годовых.

Ответ: 22,45% годовых

Задача № 42

При выдаче кредита на 2 года по простой процентной ставке 18% годовых, удерживаются комиссионные 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки сложных процентов.

Решение:

i_э=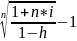 = 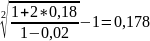, т.е. 17,8% годовых.

Ответ: 17,8% годовых.

Задача № 43

При выдаче кредита на 2 года по сложной процентной ставке 14% годовых удерживаются комиссионные 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки сложных процентов.

Решение:

i_э= 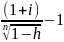= =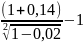0,1516, т.е. 15,16% годовых.

Ответ: 15,16% годовых.

Задача № 44

В апреле объём продаж составил 250000 руб. Себестоимость проданной продукции равна 110000 руб., а расходы (арендная плата, зарплата и т.д.) – 40000 руб. Определить валовую и чистую прибыль.

Решение:

Валовая прибыль = Объём продаж – Себестоимость проданной продукции = 250000 – 110000 = 140 000 руб.

Чистая прибыль = Валовая прибыль – Расходы = 140000 – 40000 = 100000 руб.

Ответ: 140000 руб., 100000 руб.

Задача № 45

На конец финансового года внеоборотные активы предприятия составила 120000 руб., оборотные активы – 50000 руб., краткосрочные обязательства – 60000 руб. В течение отчётного финансового года объём продаж составил 350000 руб. Определить коэффициент оборачиваемости чистых активов.

Решение:

Коэффициент оборачиваемости чистых активов = Выручка от продаж : Суммарные чистые активы;

Суммарные чистые активы = Внеоборотные активы + Оборотные активы – Краткосрочные обязательства.

Коэффициент оборачиваемости чистых активов = 3,18, т.е. за 1 год чистые активы предприятия совершают 3,18 оборота.

Ответ: 3,18 оборота.

Задача № 46

На конец финансового года запасы предприятия составили 35000 руб., дебиторская задолженность – 13000 руб., кассовая наличность – 4000 руб., краткосрочные обязательства – 58000 руб. Определить коэффициент текущей ликвидности.

Решение:

КТЛ = Оборотные активы : Краткосрочные обязательства,

КТЛ = 0,90, т.е. на 1 рубль краткосрочных обязательств приходится 0,90 руб. оборотных активов. Рекомендуемое значение КТЛ ≥ 2

Ответ: 0,90

Задача № 47

На конец финансового года запасы предприятия составили 35000 руб., дебиторская задолженность – 23000 руб., кассовая наличность – 34000 руб., краткосрочные обязательства – 68000 руб. Определить коэффициент срочной ликвидности.

Решение:

Коэффициент срочной ликвидности = (Оборотные активы – Запасы) : Краткосрочные обязательства.

Коэффициент срочной ликвидности = 0,84, т.е. на дату составления бухгалтерского баланса только 84% краткосрочных обязательств может быть погашено в короткий срок за счет оборотных активов, если запасы не представляется возможным перевести в наличные денежные средства. Рекомендуемое значение ˃1, Обычное значение: 0,7-0,8.

Ответ: 0,84.

Задача № 48

На конец финансового года средние запасы предприятия составили 35000 руб., себестоимость проданной продукции – 105000 руб. Определить коэффициент оборачиваемости запасов.

Решение:

Коэффициент оборачиваемости запасов = Себестоимость проданной продукции : Средняя величина запасов

Коэффициент оборачиваемости запасов = 3.

Ответ: 3.

Задача № 49

Средняя величина дебиторской задолженности предприятия составила 35000 руб., объём продаж в кредит – 190000 руб. Определить период оборачиваемости дебиторской задолженности. Продолжительность года составляет 360 дней.

Решение:

Период оборачиваемости дебиторской задолженности = (360* Средняя величина дебиторской задолженности) : Выручка от продаж (объём продаж в кредит).

Период оборачиваемости дебиторской задолженности = 66 дней, т.е. в среднем проходит 66 дней с момента отгрузки продукции до поступления денежных средств на счета предприятия.

Ответ: 66 дней

Задача № 50

Средняя величина кредиторской задолженности предприятия составила 45000 руб. Объём закупок в кредит – 240000 руб. Определить период оборачиваемости кредиторской задолженности. Продолжительность года составляет 360 дней.

Решение:

Период оборачиваемости кредиторской задолженности = (Средняя величина кредиторской задолженности*360) : Производственную себестоимость (объём закупок в кредит).

Период оборачиваемости кредиторской задолженности = 67,5 дней, т.е. средний срок погашения кредиторской задолженности составляет 68 дней.

Ответ: 67,5 дней.

Задача № 51

В марте закуплены для реализации 600 единиц продукции по цене 15 руб./ед. В апреле – июле проданы 450 единиц продукции по цене 25 руб./ед. В начале августа непроданная продукция была уценена до 15 руб./ ед. и по этой цене проданы 50 единиц продукции. Определить процент скидки.

Решение:

Процент скидки = (денежная сумма скидки : суммарный объём продаж)*100%.

Денежная сумма скидки = 50*(25-15) = 500 руб.

Суммарный объём продаж = 450*25+50*15 = 12000 руб.

Процент скидки = (500/12000 руб.) *100% = 4,17%.

Ответ: 4,17%

Задача № 52

Определить коэффициент рентабельности чистых активов на основании следующих данных: чистая прибыль составляет 40000 руб., внеоборотные активы предприятия – 120000 руб., оборотные активы – 50000 руб., краткосрочные обязательства – 60000 руб.

Решение:

Коэффициент рентабельности чистых активов = (Чистая прибыль : Суммарные чистые активы)* 100% = (40000 : 110000)*100% = 36,36%.

Ответ: 36,36%

Задача № 53

Определить текущую рыночную стоимость облигации при следующих данных: текущая рыночная процентная ставка составляет 18%, номинальная стоимость облигации – 5000 руб., купонная процентная ставка – 15%, оставшийся срок до погашения облигации составляет 3 года.

Решение:

Облигацию следует рассматривать как простую ренту постнумерандо, состоящую из выплат купонных процентов и возмещения номинальной стоимости облигации. Следовательно, текущая стоимость облигации равна современной стоимости этой ренты.

Величина купонных платежей (R) = k*P = 0,15*5000 = 750 руб.

Текущая рыночная стоимость облигации (A_n) = R*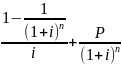 =750* +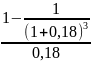

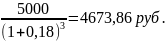
Ответ: 4673,86 руб.

Задача № 54

Облигация номинальной стоимостью - 1000 руб. с купонной процентной ставкой – 15% была приобретена в начале года за 700 руб. После получения купонного платежа в конце года облигация была продана за 750 руб. Определить норму прибыли за год.

Решение:

Норма прибыли = (купонный платёж + цена облигации в конце периода – цена облигации в начале периода) : цена облигации в начале периода

Величина купонных платежей = 0,15*1000 = 150 руб.

Норма прибыли облигации за год = (150+750 – 700) : 700 = 0,2857 или 28,57% годовых.

Ответ: 28,57% годовых.

Задача № 55

Облигация номинальной стоимостью – 1000 руб. с купонной процентной ставкой – 15% и сроком погашения – 10 лет была куплена за 800 руб. Определить доходность облигации методом средних.

Решение:

Величина купонных платежей = 0,15*1000 = 150 руб.

Общая сумма выплат = 10 лет*150 руб. + 1000 руб. = 2500 руб.

Общая прибыль = 2500 – 800 = 1700 руб.

Средняя прибыль за один период = 1700/10 = 170 руб.

Средняя стоимость облигации = (1000+800)/2 = 900 руб.

Доходность облигации = 170/900 = 0,1889 или 18,89%.

Ответ: 18,89%

Задача № 56

Номинальная стоимость облигации составляет 5000 руб., купонная процентная ставка – 15%, оставшийся срок до погашения облигации – 3 года, текущая рыночная процентная ставка составляет 12%. Определить дюрацию облигации.

Решение:

Дюрация облигации – средний срок возврата капитала для инвестора, вкладывающего средства в приобретение этой облигации.

Величина купонных платежей (R) = 0,15*5000 = 750 руб.

Поток платежей по облигации будет иметь следующий вид: S₁=S₂=R=750, S₃=R+P = 750+5000 = 5750 руб.

Дюрация (D) =

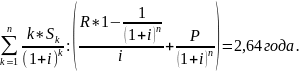
Ответ: 2,64 года.

Задача № 57

Определить коэффициент эластичности настоящей стоимости будущих доходов по ставке процента на основании следующих данных: дюрация составляет 2,634, текущая рыночная процентная ставка – 12%.

Решение:

Коэффициент эластичности показывает, на сколько процентов изменится стоимость потока фиксированных платежей по облигации при изменении ставки процента на рынке капитала на 1%.

Эластичность = D* ,282 или 28,2%

Ответ: 0,282 или 28,2%.

Задача № 58

По обращающимся привилегированным акциям выплачиваются ежегодные дивиденды в размере 50 руб. Цена акции составляет 500 руб. Определить доходность акции.

Решение:

Доходность акции = дивиденд/цена (курс) акции = 50/500 = 0,1 или 10%.

Ответ: 10%.

Задача № 59

Рыночная цена акции в настоящий момент составляет 110 руб. Ожидаемая цена акции в конце текущего года составит 120 руб. ожидаемый дивиденд в текущем году будет равен 5 руб. Определить ожидаемую дивидендную доходность, ожидаемую доходность за счёт изменения цены акции и ожидаемую доходность по акции в текущем году.

Решение:

Ожидаемая дивидендная доходность в текущем году = 5/110 = 0,05 или 5%.

Ожидаемая доходность за счёт изменения цены акции = (120-110)/110 = 0,091 или 9,1%.

Ожидаемая доходность по акции в текущем году = 5%+9,1% = 14,1%.

Ответ: 14,1%

Задача № 60

Дивиденд, выплачиваемый ежегодно по акции нулевого роста, равен 300 руб. Ожидаемая норма прибыли составляет 8%. Определить внутреннюю (теоретическую) цену акции.

Решение:

Внутренняя (теоретическая) цена акции нулевого роста представляет собой текущее значение бессрочной ренты постнумерандо. Она определяется по формуле: в числителе – дивиденд, выплачиваемый ежегодно по акции нулевого роста, а в знаменателе – ожидаемая норма прибыли.

300/0,08 = 3750 руб.

Ответ: 3750 руб.

Задача № 61

Курс акции нулевого роста в настоящий момент составляет 300 руб., а последний из уже выплаченных дивидендов составил 15 руб. Определить норму прибыли (доходность) акции.

Решение:

Норма прибыли (доходность) акции нулевого роста определяется отношением: в числителе – последний из уже выплаченных дивидендов, а в знаменателе – курс акции нулевого роста в настоящий момент времени.

15/300 = 0,05 или 5%.

Ответ: 5%.

Задача № 62

Последний из уже выплаченных дивидендов по акциям нормального роста составил 450 руб., а ожидаемый темп роста дивидендов равен 5%. Определить дивиденд, который акционер ожидает получить в текущем году.

Решение:

Дивиденд в текущем году = Последний из уже выплаченных дивидендов *(1+ожидаемый темп роста дивидендов)^t, где t – период за который акционер ожидает получить дивиденд.

450*(1+0,05)¹ = 472,5 руб.

Ответ: 472,5 руб.

Задача № 63

Период избыточного роста (N) составляет 4 года, темп роста доходов и дивидендов в течение периода избыточного роста (g_s) составляет 25%, постоянный темп роста после периода избыточного роста (g_n) составляет 10%, последний из уже выплаченных дивидендов (D₀) составляет 450 руб., требуемая норма прибыли (k_s) 14%. Определить внутреннюю (теоретическую) цену акции избыточного роста (P₀^/).

Решение:

Теоретическая (внутренняя) цена акции избыточного роста (P₀^/) =

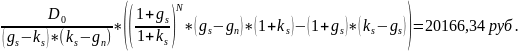
Ответ: 20166,34 руб.

Задача № 64

Чистая прибыль после уплаты налогов составляет 150000 руб., а число обыкновенных акций равно 6000. Определить прибыль на акцию.

Решение:

Прибыль на акцию = 150000/6000 = 25 руб.

Ответ: 25 руб.

Задача № 65

Чистая прибыль после уплаты налогов составляет 150000 руб., а число обыкновенных акций равно 6000, общая сумма дивидендов составляет 90000 руб. Определить дивиденд на акцию.

Решение:

Дивиденд на акцию = 90000/6000 = 15 руб. на акцию

Ответ: 15 руб.

Задача № 66

Чистая прибыль после уплаты налогов составляет 150000 руб., а число обыкновенных акций равно 6000, общая сумма дивидендов составляет 90000 руб. Определить коэффициент дивидендного покрытия.

Решение:

Прибыль на акцию = 150000/6000 = 25 руб.

Дивиденд на акцию = 90000/6000 = 15 руб.

Коэффициент дивидендного покрытия = 25/15 = 1,67, т.е. выплата дивидендов подкреплена прибылями на 1,67 за год или же в течение года дивиденды могли бы быть выплачены 1,67 раз.

Ответ: 1,67.

Задача № 67

Чистая прибыль после уплаты налогов составляет 150000 руб., а число обыкновенных акций равно 6000, общая сумма дивидендов составляет 90000 руб., текущая рыночная цена акции составляет 300 руб. Определить коэффициент доходности дивидендов.

Решение:

Дивиденд на акцию (последний выплаченный дивиденд на акцию) = 90000/6000 = 15 руб.

Коэффициент доходности дивидендов = 15/300 = 0,05*100% = 5%.

Ответ: 5%.

Задача № 68

Предприятие выпустило акций на сумму 200000 руб. и взяло долгосрочную банковскую ссуду на 100000 руб. Определить леверидж.

Решение:

Используемый капитал = акционерный капитал+долгосрочные заёмные средства = 200000+100000=300000 руб.

Леверидж = используемый капитал/акционерный капитал = 300000/200000 = 1,5, т.е. общая сумма средств, инвестированных в предприятие в 1,5 раза превышает средства полученные за счёт выпуска акций.

Ответ: 1,5.

Задача № 69

Предприятие выпустило акций на сумму 200000 руб. и взяло долгосрочную банковскую ссуду на 100000 руб. Чистая прибыль предприятия в истекшем году составила 70000 руб. За взятую ссуду предприятие ежегодно платит 14%. Определить коэффициент рентабельности акционерного капитала.

Решение:

Процент по ссуде = 0,14*100000 = 14000 руб.

Коэффициент рентабельности акционерного капитала = (чистая прибыль – процент по ссуде)/акционерный капитал = (70000 – 14000)/200000 = 0,28.

Ответ: 0,28.

Задача № 70

Совокупные затраты составляют 150000 руб., число проданных единиц продукции составляет 6000. Определить средние затраты на единицу проданной продукции.

Решение:

Средние затраты на единицу проданной продукции = совокупные затраты/число проданных единиц продукции = 150000/6000 = 25 руб./ед.

Ответ: 25 руб./ед.

Задача № 71

Постоянные затраты составляют 40000 руб., цена реализации единицы продукции 80 руб., переменные затраты на единицу продукции 55 руб. Определить точку безубыточности.

Решение:

Точка безубыточности = 40000/(80-55) = 1600 единиц.

Ответ 1600 единиц.

Задача № 72

Объём реализации продукции равен 600 единиц, точка безубыточности 500 единиц. Определить предел безопасности.

Решение:

Предел безопасности = (объём реализации – точка безубыточности) : точка безубыточности = (600 – 500)/500 = 0,2.

Ответ: 0,2.

Задача № 73

Предприятие имеет возможность инвестировать 3 млн. руб. Рассматриваются следующие инвестиционные проекты, поддающиеся дроблению (денежные поступления со знаком «+», денежные оттоки со знаком «-»): проект А (-1,9;0,8;0,9;1,2), проект Б (-2,1;0,7;1,1;1,3), проект В (-1,6;0,5;0,8;1,4). Альтернативные издержки по инвестициям составляют 11%. Определить оптимальный инвестиционный портфель.

Решение:

Найдём индекс рентабельности каждого инвестиционного проекта:

Проект А = приведённая стоимость денежных поступлений / приведённая стоимость денежных оттоков = (0,8/1,11+0,9/1,11²+1,2/1,11³)/1,9 = 1,226

Проект Б = (0,7/1,11+1,1/1,11²+1,3/1,11³)/2,1 = 1,178

Проект В = (0,5/1,11+0,8/1,11²+1,4/1,11³)/1,6 = 1,327

Ранжируем инвестиционные проекты по убыванию индекса рентабельности: Проект В (1,327), Проект А (1,226), Проект Б (1,178). Так как предприятие может инвестировать только 3 млн. руб., то проект В будет профинансирован полностью, а проект А лишь частично на сумму (3 млн. руб. – 1,6 млн. руб.) = 1,4 млн. руб.

Ответ: проект В профинансирован полностью, а проект А лишь частично на сумму 1,4 млн. руб.

Задача № 74

Взят кредит под 11% годовых. Ставка налога на прибыль составляет 35%. Определить стоимость кредита после налогообложения.

Решение:

Стоимость кредита после налогообложения = стоимость кредита до налогообложения * (1 – ставка налога на прибыль).

Стоимость кредита после налогообложения = 0,11*(1-0,35) = 0,0715 или 7,15% годовых.

Ответ: 7,15% годовых.

Задача № 75

Рыночная цена акции в настоящий момент времени составляет 500 руб. Ожидается, что дивиденд в текущем году будет равен 60 руб., а постоянный темп роста дивидендов составит 4%. Определить стоимость акционерного капитала.

Решение:

Стоимость акционерного капитала = (ожидаемый дивиденд в текущем году : рыночную цену акции в настоящий момент времени) + постоянный темп роста дивидендов.

Стоимость акционерного капитала = 60/500 + 0,04 = 0,16 или 16%.

Ответ: 16%.

Задача № 76

Определить средневзвешенную стоимость капитала (WACC) предприятия на основании следующих данных:

Источник капитала	Стоимость	Рыночная стоимость
Кредит	11	0,6
Обыкновенные акции	15	1,8
Облигационный займ	9	0,5

Решение:

Источник капитала	Стоимость	Рыночная стоимость	Доля в рыночной стоимости
1	2	3	4	5
Кредит	11	0,6	0,207	2,277
Обыкновенные акции	15	1,8	0,621	9,315
Облигационный займ	9	0,5	0,172	1,548
Сумма	-	2,9	1	WACC = 13,14% годовых

В последней строке указана сумма соответствующего столбца. Каждое число 3-его столбца делим на сумму чисел этого столбца, результат округляем до трёх цифр после запятой и записываем в 4-м столбце. 5-тый столбец – это произведение 2-го и 4-го столбцов.

Ответ: WACC = 13,14% годовых.

Задача № 77

Чистая прибыль после уплаты налогов составляет 150000 руб., число обыкновенных акций равно 6000. Определить прибыль на акцию.

Решение:

Прибыль на акцию = чистая прибыль после уплаты налогов : число обыкновенных акций = 150000 : 6000 = 25 руб. на акцию.

Ответ: 25 руб. на акцию

Задача № 78

Чистая прибыль после уплаты налогов составляет 150000 руб., число обыкновенных акций равно 6000. Прибыль до выплаты процентов и налогов составляет 200000 руб., проценты к уплате 40000 руб., ставка налога на прибыль 25%. Определить прибыль на акцию.

Решение:

Прибыль на акцию = (прибыль до выплаты процентов и налогов – проценты к уплате) * (1- ставка налога на прибыль) : число обыкновенных акций = (200000 – 40000)*(1-0,25) : 6000 = 20 руб. на акцию

Ответ: 20 руб. на акцию.

Задача № 79

Текущая прибыль предприятия до выплаты процентов и налогов равна 2,1 млн. руб., проценты по текущим долгам 0,5 млн. руб., число обыкновенных акций составляет 5500, ставка налога на прибыль 40%. Предприятию требуется 2,9 млн. руб. для финансирования инвестиционного проекта, который, как ожидается, увеличит на 0,7 млн. руб. ежегодную прибыль предприятия до выплаты процентов и налогов. Рассматриваются следующие варианты: 1) выпуск 1000 акций; 2) кредит под 11% годовых. Определить, что является наиболее выгодным для акционеров.

Решение:

Прибыль на акцию = (прибыль до выплаты процентов и налогов – проценты к уплате) * (1- ставка налога на прибыль) : число обыкновенных акций.

В случае выпуска акций прибыль на акцию составит: (х-0,5)*(1-0,4)/(5500+1000).

В случае кредита прибыль на акцию составит: (х-0,5-2,9*0,11)*(1-0,4)/5500.

Приравняем полученные значения прибылей на акцию при выпуска акций и кредита, получим: (х-0,5)*0,6/6500 = (х-0,181)*0,6/5500, т.е. точка безразличия (х) = 2,2545.

Ожидаемая ежегодная прибыль предприятия до выплаты процентов и налогов составит: 2,1 млн. руб. + 0,7 млн. руб. = 2,8 млн. руб. Это превосходит значение точки безразличия (2,25), следовательно, прибыль на акцию будет выше в случае кредита.

Ответ: кредит выгоднее.

Задача № 80

Доходность ценных бумаг с нулевым риском (R_f) составляет 5%, доходность акций рыночного индекса (R_m) – 12%, показатель риска акций компании по отношению к портфелю ценных бумаг, присутствующих на рынке (β) равен 0,8. Определить доходность обыкновенных акций (k_e) компании.

Решение:

k_e = R_f + β*(R_m - R_f) = 0,05+0,8*(0,12 – 0,05) =0,106 или 10,6%.

Ответ: 10,6%.

Задача № 81

Известны курсы А/В 34,75-34,95; С/В 29,85-29,95. Определить курс А/С.

Решение:

Курс покупки А/С = (курс покупки А/В)/(курс продажи С/В) = 34,75/29,95 = 1,16

Курс продажи А/С = (курс продажи А/В)/(курс покупки С/В) = 34,95/29,85 = 1,17

Курс А/С = 1,16 – 1,17.

Ответ: 1,16-1,17.

Задача № 82

Известны курсы А/В 0,84-0,89; А/С 29,75-29,95. Определить курс В/С.

Решение:

Курс покупки В/С = (курс покупки А/В)/(курс продажи А/С) = 0,84/29,95 = 0,028

Курс продажи В/С = (курс продажи А/В)/(курс покупки А/С) = 0,89/29,75 = 0,030

Курс В/С = 0,028 – 0,030.

Ответ: 0,028 – 0,030.

Задача № 83

Известны курсы А/В 1,15-1,18 и В/С 29,75-29,95. Определить на основании этих данных курс А/С.

Решение:

Курск покупки А/С = (курс покупки А/В)*(курс покупки В/С) = 1,15*29,75 = 34,21

Курс продажи А/С = (курс продажи А/В)*(курс продажи В/С) = 1,18*29,95 = 35,34

Курс А/С = 34,21 – 35,34

Ответ: 34,21-35,34.

Задача № 84

Курс А/В: спот 35,60-35,95; 1 месяц 30-50. Найти курс форвард.

Решение:

Так как 30˂50, то валюта А котируется с премией по отношению к валюте В. Для определения курса форвард эту премию прибавляют к курсу спот. Ожидаемый курс А/В через 1 месяц будет равен 35,90 – 36,45.

Ответ: 35,90-36,45.

Задача № 85

Приобретён опцион на покупку через месяц валюты А по следующей цене: 1 денежная единица А равна 35,25 денежных единиц В с выплатой премии равной 0,1 денежных единиц В за 1 денежную единицу А. Определить результаты сделки, если через 1 месяц курс А/В составит: 1) 35,45-35,65; 2) 35,05-35,15.

Решение:

Если через месяц курс А/В составит 35,45-35,65, то сложившийся рыночный курс продажи валюты А будет равен = 35,65. Так как 35,25˂35,65, то опцион реализуется при эффективном курсе обмена равном = 35,25+0,1 = 35,35.

Если через месяц курс А/В составит 35,05-35,15, то сложившийся рыночный курс продажи валюты А равен = 35,15. Так как 35,25˃35,15, то следует отказ от реализации опциона и эффективный курс обмена = 35,15+0,1=35,25.

Ответ: опцион реализуется эффективный курс обмена 35,35; отказ от реализации опциона эффективный курс обмена 35,25.

Задача № 86

Годовой спрос (D) составляет 400 единиц, стоимость подачи заказа (C₀) 40 руб./заказ, издержки хранения одной единицы (C_h) составляют 250 руб./ год, время доставки 6 дней, 1 год равен 250 рабочих дней. Определить оптимальный размер заказа, издержки, уровень повторного заказа, число циклов за год и расстояние между циклами.

Решение:

Оптимальный размер заказа:

q=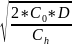 = 11 единиц.

Издержки = 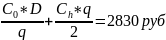/год.

За 250 рабочих дней реализуется 400 единиц, за 6 дней доставки – х единиц, следовательно, 250/6 = 400/х, отсюда х = 400*6/250 = 10 единиц.

Каждый раз когда на складе остаётся 10 единиц, совершается заказ на 11 единиц.

Годовой спрос составляет 400 единиц, каждый раз заказывается 11 единиц, следовательно, за год будет подано = 400/11=36 заказов или 36 циклов.

Расстояние между циклами = 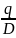*количество рабочих дней в году = 11/400*250 = 7 рабочих дней.

Ответ: оптимальный размер партии = 11 единиц; издержки за год = 2830 руб.; остаток на складе 10 единиц; число циклов = 36; расстояние между циклами = 7 рабочих дней.

Задача № 87

Годовой спрос (D) составляет 8000 единиц, стоимость организации производственного цикла (C_s) равна 200 рублей, издержки хранения одной единицы (C_h) составляют 15 рублей/год. Определить экономичный размер партии, издержки, число циклов за год и расстояние между циклами.

Решение:

Экономичный размер партии составляет: q=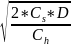 = 462 единицы, т.е. необходимо произвести 462 единицы, остановить производство, реализовать всю продукцию и вновь запустить производство и т.д.

Издержки составляют: 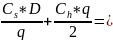6928 руб./ год.

Число циклов за год = 8000/462 = 17,32.

Расстояние между циклами = 462/8000 = 0,058 лет = 0,058*365 (число дней в году) = 21 день.

Ответ: 462 ед., 6928 руб./год, 17,32 цикла, 21 день.

Задача № 88

Годовой спрос составляет 1200 единиц, стоимость подачи заказа равна 50 рублей/заказ, закупочная цена составляет 60 рублей/единицу, годовая стоимость хранения одной единицы составляет 35% её цены. Если размер заказа будет не меньше 90 единиц, то у поставщиков можно будет получить скидку в размере 5%. Определить, стоит ли воспользоваться скидкой.

Решение:

Задача № 89

Средневзвешенная стоимость капитала предприятия составляет 12%. Прогноз прибыли предприятия после налогообложения по годам соответственно составляет: 60000 руб., 70000 руб. и 80000 руб. Предполагается, что с четвёртого года предприятие будет расти ежегодно на 6%. Прогноз суммарных чистых активов предприятия по годам соответственно составляет 260000 руб., 280000 руб. и 300000 руб. Определить экономическую добавленную стоимость предприятия.

Решение:

Задача № 90

Переоценённая рыночная стоимость материальных активов предприятия составляет 600000 руб., отраслевой коэффициент отношения чистой прибыли к собственному капиталу – 11%, среднегодовая чистая прибыль предприятия за последние пять лет – 80000 руб., коэффициент капитализации прибылей предприятия – 14%. Определить стоимость гудвилла предприятия.

Задача № 92

Предполагается, что объём продаж увеличится на 1,5 млн. руб. и составит 9 млн. руб. Предприятие способно обеспечить 85% объёма продаж за счёт собственных источников. Остальная часть объёма продаж будет обеспечена за счёт заёмного капитала. Рентабельность составляет 10%. Не распределяемая по дивидендам доля прибыли равна 50%. Определить величину дополнительного финансирования.

Решение:

Дополнительное финансирование = (предполагаемое увеличение объёма продаж)*(доля объёма продаж, которую предприятие обеспечит из собственных источников – доля объёма продаж, которую предприятие обеспечит за счёт заёмного капитала) – (предполагаемый объём продаж)*(рентабельность)*(не распределяемая по дивидендам доля прибыли) = 1,5*(0,85 – 0,15) – 9*0,1*0,5 = 0,6 млн. руб.

Ответ: 0,6 млн. руб.

Задача № 93

Объём продаж предприятия составляет 900000 руб., число работников предприятия – 130 человек. Определить объём продаж на одного работника.

Решение:

900000/130 = 6923,08 руб.

Ответ: 6923,08 руб.

Задача № 94

Центральный банк выкупает у коммерческих банков государственные ценные бумаги на сумму 6 млрд. руб. Норма обязательных резервов составляет 20%. Определить, как изменится денежная масса.

Решение:

Величина мультипликатора = 1/ (норма обязательных резервов) = 1/0,2 = 5.

Денежная масса увеличится на 5*6 млрд. руб. = 30 млрд. руб.

Ответ: увеличится на 30 млрд. руб.

Задача № 95

В условиях «перегрева» экономики центральный банк повысил учётную ставку с 9% до 12% и предложил к учёту векселя на сумму 150000 руб. Норма обязательных резервов составляет 12%. Определить, как изменится денежная масса.

Решение:

При повышении учётной ставки цена векселей понижается. Поэтому коммерческие банки заинтересованы в приобретении векселей. Это позволит банкам в дальнейшем реализовать векселя по номиналу.

Величина мультипликатора = 1/ (норма обязательных резервов) = 1/0,12 = 8,33. Тогда денежная масса уменьшается на 150000*8,33 = 1249500 руб.

Ответ: уменьшится на 1249500 руб.

Задача № 96

Фирма-импортёр обращается в банк с заявкой на покупку валюты А через 3 месяца (91 день) в обмен на валюту В. На валютном рынке на момент заключения сделки курс А/В: спот 20,15-20,25; 3 месяца 15-20. Ставки на денежном рынке на 91 день: 2-4% годовых (валюта А) и 5-7% годовых (валюта В). Прибыль банка должна составлять 0,1% от суммы сделки в валюте В. Определить курс форвард продажи валюты А для фирмы.

Решение:

Банк для исключения своего риска может провести своп с валютой А: займ валюты В под i_В = 14% годовых, конвертация её в валюту А по курсу спот R_S = 29,50, размещение валюты А на депозите под i_A = 5% годовых с одновременным заключением форвардной сделки по продаже валюты А фирме.

Проценты получаемые от депозита валюты А, предполагается обменять на валюту В с помощью форвардной сделки с другим банком по курсу форвард R_fb = 29,35+0,35 = 29,70. Норма прибыли за 91 день равна 0,5%, а за 360 дней – g%. Следовательно, 91/360 = 0,5/g, т.е. g = 360*0,5/91 = 2% годовых.

Тогда курс форвард продажи валюты А для фирмы будет равен = R_S*(1+i_B*t/360 + g) – R_fb*i_A*t/360 = 29,50*(1+0,14*91/360)+0,02) – 29,70*0,05*91/360 = 30,76.

Ответ: 30,76.

Задача № 97

Инвестор приобрел привилегированные акции банка «Сигма» номиналом 500 руб. по цене 550 руб. Через три года он продал эти акции по курсу 614,5 руб. Дивиденд по акциям равнялся 10% годовых. Определить конечную доходность акций за весь инвестиционный период.

Решение:

Сумма выплаченных дивидендов за год оставляла 500 * 0,1 = 50 руб., а за три года 150 руб. Изменение курсовой стоимости составило: 614,5 – 550 = 64,5 (руб.). Конечная доходность: (150 + 64,5) / 550 = 0,39 за три года или 0,39 / 3 = 0,13 или 13% годовых.

Ответ: конечная доходность составила 13 % годовых.

АО зарегистрир 10 тыс обык акций. 9 тыс продали акционерам. Потм выкупили 500 акц.

По окончании отчетного периода приняли решение о распредел дивидентов в сумме 1,7 млн прибыли. Опр дивид на 1 акц.

1,7 млн/8500=200 руб/акц.

Акция номиналом 1000 руб куплена по курсу 250%. По ней выплачивается дивидент 50%. Опр текущ дох-ть.

К=250%= P*100%/P_н => P=2500; 50%* P_н/2500=500*100%/2500=20%.

Банк выдал ссуду 18 янв 50 млн руб. Срок возврата 3 марта. Проц ставка 80% годовых. Опр наращ сумму.

S=P(1+i*n); S=50млн(1+ 45*0,8/365)=54,931 млн.

Банк предлаг вкладч услов по сроч годов депоненту: в 1-ое полугод i=0,8 год-х. Кажд след квартал ставка возраст на 8%. Опр наращ за год сумму, если Р=500 тыс руб.

S=500 тыс(1+0,8*0,5+0,25(0,8+0,08)+0,25(0,8+0,16))=930 тыс.

Банк выпустил депозит сертиф с номиналом в 1 млн руб сроком на 6 мес (181дн) по ставке 10 %

год-х. Инвестор, имеющий сертификат, продает его через 90 дн после приобретения. Опр эф-ть сделки, если в момент вторич продажи % ставка была 9%(год=360). Опр прибыль в 1 и во 2 случае.

Конечная ст-ть 1 млн (1+0,1*181/360)=1,052 млн; дисконтир на 90 день S/(1+d*n) = 1,052/(1+0,09*91/360) = 1,027 млн.

Банк предоставил клиенту кредит на 3 мес с 15.05 по 15.08 под залог 200-х сот акций. Курсовая ст-ть в день выдачи кредита=20 тыс руб за акц. Сумма кредита составляет 75% курс ст-ти залога. Кредит выдается под 20% год-х. Обслуж долга 1% от номин суммы кредита. % взимаются сразу. Опр размер получен кредита.

Сумма 4000*0,75=3000 =S; %=3000*20%/4=150 руб; за обслужив долга 3000*1%=30 руб. Всего 180 руб. Кредит 3000-180=2820 руб

Банк выдал кредит 5 млн на 6 мес. Уров инф (месяч)-2%. Требуемая дох-ть операции 10% г-х. Опр наращенную сумму.

i_инф=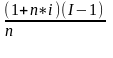 ; I=(1+0,02)^6; i_инф= ;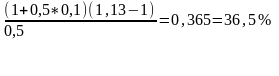

5 млн (1+0,5*0,365)=5,91 млн –наращ сумма.

Банк принимает вклады до востреб под 8,84%. Год =365 дн. Какую учет ставку должен применить банк при учете векселя в день его погашения, чтобы обеспечить дох-ть= по вкладам до востребов. Срок обращ векселя 200дн (в году 360 дн).

1+0,0848*200/365=1/(1-200*d/360) => d=0,0799. Почти 8%.

Банк выдал долгосроч кредит 400 млн на 5 лет под 6% год-х. Погашение кредита производится равными ежегодными выплатами, включ погашен основ долга и % платежи. Сост план погашен кредита.

Y=D*i*(1+i)ⁿ/((1+i)ⁿ-1); F=(Y-I); n=5; I=D*0,06; D_i=D_i-1-F;

Y=400 млн*0,06*(1,06)⁵/((1,06)⁵-1) = 95 млн.

годы	остат долга(D)	% платеж(I)	годов расход(F)	годов сроч упл(Y)
1	400 млн	24 млн	71 млн	95 млн
2	329 млн	19,74 млн	75,26 млн	95 млн
3	253,74 млн	15 млн	80 млн	95 млн
4	173,74 млн	10,4 млн	84,6 млн	95 млн
5	89,14 млн	5,4 млн	89,6 млн	95 млн

Вексель номин. ст-тью 500т руб был учтен в банке за 90 дней дл срока погашения по учёт ставке 16%. Опр. дисконтир. величину векселя, либо опр сумму, по котор будет учтен вексель в банке.

P=S(1-dn)

P=500т(1-0,16*90/365)=480274; Д=S-P=500 тыс-480274=19726.

Вексель выдан на сумму 1 млн руб с уплатой 17 нояб. Владелец векселя учел его в банке 23 сент по учет ставке 20%. Опр дисконт.

S=1 млн; d=20%; n=55дн;

D=S*n*d/355.

Вексель учтен в банке по учет ставке 8% в день окончан срока обращ =200 дн. Опр доходность операции.

.

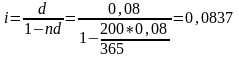В контракте предусмотрено погашен обязат-в в сумме 110 млн через 120 дн. Первонач сумма долга 90 млн. Опр дох-ть операции, если использов-ся антисепативный метод.

S=P/(1-d*n) => 110 млн=90 млн/(1-d/3); d=6/11=0,54.

Выдан кредит 250 млн на 5 лет под 20% год-х. Погашение кредита производится равными выплатами в конце основ кредита. Сост план погашен кредита.

К табл-все в млн.

годы	остат долга(D)	% платеж(I)	годов расход(F)	годов сроч упл(Y)
1	250	50	50	100
2	20	40	50	90
3	150	30	50	80
4	100	20	50	70
5	50	10	50	60

Выдан кредит 400 млн на 5 лет под 15% год-х. Начислен в конце выплаты основ долга. Сост план погашен кредита.

К табл-все в млн.

годы	остат долга(D)	% платеж(I)	годов расход(F)	годов сроч упл(Y)
1	400	60	60	120
2	340	51	70	121
3	270	40,5	80	120,5
4	190	28,5	90	118,5
5	100	15	100	115

Депозит в размере 500 тыс руб внесен в банк на 3 года под 10% год-х (% слож). Начислен ежекварт.

S=P(1+i/n)^tn =500 тыс(1+0,1/4)^3*4=672444.

Долговое обязательство в сумме 2 млн руб должно быть погашено через 90 дней с 120%. Владелец обяз-ва учел его в банке за 15 дн до срока по учет ставке 135%. Опр. полученную при учете сумму.

2 млн(1+90*1,2/365)(1-15*1,35/365)=2,448 млн.

Долговое обязательство в сумме 2 млн руб должно быть погашено через 90 дней с 120%. Владелец обяз-ва учел его в банке за 15 дн до срока по учет ставке 135%. Опр. полученную при учете сумму.

2 млн(1+90*1,2/365)(1-15*1,35/365)=2,448 млн.

Кредит в 10 млн выдан на 2 года. Реальная дох-ть должна состав-ть 11% год-х (% слож). Расчет уровень инф-ции 16%в год. Опр наращ сумму.

i_инф= i+α+i*α=0,11+0,16+0,11*0,16=0,2876; 10 млн(1+0,2876)²=16,576 млн;

наращ сумма - 6 млн 576 тыс.

Кредит обязат =40 млн руб со сроком погашения через 4 года было учтено в банке по учет ставке 8% год-х. Начислен дисконта по полугод. Опр современн величину обязат-ва.

P=S(1+d)^n=40 млн(1+0,04)^8=28,8 млн.

Клиент обратился в банк за кредитом 8 млн на 270 дн. Банк предоставил кредит на след усл: 20% год-х должны быть начисл и выплачен в момент его выдачи. Опр сумму полученного кредита.

P=S(1-dn); 8 млн(1-0,2*270)=6,8 млн.

Какова эф ставка, если номин ставка=25% при месячном начисл %.

P(1+j/m)^n*m =P(1+i_эф)ⁿ => i_эф = (1+0,25/12)¹²-1=0,28.

Каков сред курс DM/швейц франк на основе сред курсов: 1$=2,02DM; 1$=1,86 швейц франков.

Решение: х швейц франков=100DM; 100DM=1,86*100/2,02=92,43 швейц франков.

Купонная дох-ть облигации g=11,75%. Курс облиг 95. Опр текущ дох-ть облиг.

Дох-ть= доход/влож. капитал =g*N(номин)/р(р.ц.)=11,75*100%/95=12,37%.

Номин акц 1000 руб. Дох-ть 40% год-х. Курсов цена через год после эмиссии 2 тыс руб.Опр конеч дох-ть.

дох-ть 400 + измен (2 тыс-1 тыс)=1400; 1400/1000=140%.

На какую годов ставку прост % можно заменить слож годовую ставку =20 %, если начислен производ ежиквартально в течение 2-х лет.

P(1+2*i)=P(1+0,05)⁸; 1+2*i=1,48 =>i=0,24 или 24%.

Опр эф ставку слож %, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки 18% при ежеквартальн начислен %.

i_э= (1+0,18/4)⁴-1=0,1925 или 19,25%.

Опр значение учет ставки, эквивалентной ставке прост %=120% год-х при сроке ссуды 1 год.

d=i/(1+i*n)=1,2/1+1,2=0,54 (54%).

Опр доход владельца банковского векселя, если он продал бумагу за 30 дн до погашения. Рыноч ставка по месячным векселям 60%.

Потери: 60/12=5%, 10000*0,05=500; доход: 10000-8260-500=1240.

Опр доходы банков и переучетов. Сумма векселей 100 тыс. Учет производится коммер банком за 72 дня до даты погашения по ставке 8%. Переучет ЦБ за 30 дн до погашен по ставке 6%.

P=S(1-d*n)=100тыс(1-0,08*72/365)=1578,22; Д^’=100тыс*0,08*72/365=1600-дисконт для влад векселя; Д^’’=100тыс*0,06*30/365=493,15-дисконт для ЦБ; 1600-493,15- дисконт для КБ.

Опр дох-ть операции, в котор ожидаемое соотношение курсов валюты в руб за 2 года опр как 1900/1100. Вложение конвертир средств произв-но по 100% год-х (% слож).

S=P*K₁(1+i)ⁿ/K₂ => S=P*1000(1+i)²/1900=40*P/19; S=P(1+i)² => 40/19=(1+i)² => 1+i=1,45 => i=45%

Предполаг поместить 1тыс$ на руб депозит. Курс продажи на начало срока депозита 1500, ожидаемый курс покупки 1820, i=220%, срок депозита 3 мес.

1000*1500(1+220*3/100*12)/1820=1277,47.

Период размещения векселя с 11.01 по 24.01. Дата погашен 03.05 след года. Цена размещен не изменена в течении всего срока=8260. Номинал (S) 10 тыс. Опр дох-ть векселя в 1 и послед день размещения.

1. купили 11.01 => i=(S-P)*365/(P*112)=0,6865.

Получен кредит в сумме 10 млн на 7 лет. % ставка изменяется: 1 и 2 год-7%, 3-4г-10%, 5-7г-16%. Сост план погашен кредита (% выплачив в конце года).

Y₁=D*0,07*(1,07)⁷/((1,07)⁷-1)=1,85 млн,

Y₃=Y₄=D₃*0,1*(1,1)⁵/((1,1)⁵-1)=2 млн,

Y₅=D₅*0,16*(1,16)³/((1,16)³-1)=2,2 млн. К табл-все в млн.

годы	остат долга(D)	% платеж(I)	годов расход(F)	годов сроч упл(Y)	% ставка(i)
1	10	0,7	1,15	1,85	0,07
2	8,85	0,6195	1,23	1,85	0,07
3	7,62	0,762	1,238	2	0,1
4	6,382	0,6382	1,3618	2	0,1
5	5,0202	0,803232	1,4	2,2	0,16
6	3,6	0,576	1,624	2,2	0,16
7	1,976	0,31616	1,88	2,2	0,16

Планируется выпуск займа на сумму 2 млн. Весь займ разделен на 100 облигаций. Требуется погасить займ за 4 года одинак годов выплатами. Облиг имеют купонную дох-ть 5%, выплачив 1 раз в год. Погашен облиг происходит по номинальн ст-ти.

годы	годов сроч упл(Y)	% платеж(I)	Сумма, предл на выкуп обл.	Число непогашен обл на начало	в конце
1	564	100	464	100	23
2	564	77	487	77	24
3	564	53	511	53	26
4	564	27	537	27	27

Рос импортер должен заплатить поставщику из Гонконга 300 тыс $г. Рос банк установил курс 4500 руб=1$; 1$=7,75$г. Ск-ко должен рос импортер денег?

300000*4500/7,75=174,193 млн.$г.

Рос экс-имп компания поставила свой товар во Фран на сумму 1,685 млн FRF . И одновременно закупила товар в Англии, за котор должна заплатить 200 тыс ANF. 1$=5,13FRF; 1ANF=1,54$. Опр часть суммы от продажи во франках.

Уплачено: 200 тыс*1,54=308 тыс$ => 308 тыс*5,13=1580040 FRF. Остаток: 1685000- 1580040=104960 FRF.

Фирма планир получ кредита в сумме 10 млн руб. Банк предоставл под 200% год-х. На какой срок фирма может взять кредит, чтобы долг не превышал 15 млн.

S=P(1+2*n)=>15 млн =10 млн(1+2*n)=> n=0,25.

Фирма получ кредит на P=10 млн на 5 лет, для 1 года i=10,5%, для 2 года маржа 1,5%, для 3 года и т. д.-0,75%. Опр сумму долга, подлеж погашению (% слож).

S=P(1+i₁)(1+i₂)(1+i₂+0,0075)³=17,739 млн.

Фирма получила в банке ссуду, под обеспечен котор выдала вексель номин стоим S₀=2 млн руб и сроком погашения 01.04. В день погашения векселя фирма обратилась в банк с просьбой об изменении порядка погаш долга. Банк соглас на след услов: фирма выдает 2 векселя на S₁=200 тыс срок погаш 08.06 и на S₂=400 тыс срок погаш 18.06. И ещё 2 векселя одинакового, но неизвестного номинала сроком погаш 01.05 и 17.05. Опр номин стоим этих векселей, если учет ставка 12%.

S₀=S₁(1-68*i/365)+S₂(1-78*i/365)+S₃(1-30*i/365)+S₄(1-46**i/365) =>

2.000.000=200(1-68*0,12/365)+400(1-78*0,12/365)+X(1-30*0,12/365)+X(1-46*0,12/365)=716.

Фирма получила кредит на сумму 900 тыс руб под 10% годовых. Кредит должен быть погашен двумя платежами: 500 тыс с % через 90 дн и 400 тыс с % через 120 дн. Впоследствии фирма договорилась с кредитором об объединении платежей в один сроком погашения через 150 дн (год=360 дн). Опр размер платежа.

1 плат=500 тыс (1+0,01*90/360)=512,5 тыс; 2 плат=400 тыс(1+0,01*120/360)=413,2 тыс;

за 1плат: 512,5 тыс (1+0,01*60/360)=521 тыс; за 2 плат: 413,2 тыс (1+0,01*30/360)=416,6 тыс;

всего: 521 тыс+416,6 тыс=937,6 тыс.

Фирма заплатила банку 523 тыс за предоставленный на 90 дн кредит 500 тыс под 20% год-х (% слож, 365 дн). Опр размер учет ставки для получения банком равноцен суммы.

500 тыс = 523 тыс(1-d)^90/365 => d=15%.

Через 1 год владелец векселя должен получить 220 тыс. Какая сумма была внесена, если дох-ть векселя 120% год-х.

P=S/(1+i*t)=>220 тыс/2,2=100 тыс.

Через 180 дн после подписан договора должны уплатить 310 тыс руб. Кредит выдан под 16%. Какова первонач. сумма долга?

S=P(1+ n*i/365) =>P=287328.

УК АО =10 млн раздел на 900 обык и 100 привил акц. Размер прибыли к распредел 2 млн. Ставка по привил акц 20%. Опр дивид по привил и обык акц.

10 млн/ 1000 акц = 10 тыс –ст-ть кажд акц. На прив: 0,2*10 тыс= 2тыс, по всем привил акц 100*2 тыс =200 тыс, (2 млн-200тыс)/900=2 тыс на обык акц.

Микроэкономика

Задача № 1

Спрос и предложение рынка описываются уравнениями:

P=20000-40*Q

P=60*Q

Дайте подтвержденную расчетами оценку изменения стоимости товарооборота (выручки) рынка если предложение уменьшится

Решение задачи № 10:

1 . Из контекста условия задачи уменьшение предложения выражается перемещением зависимости спроса влево (или вверх)

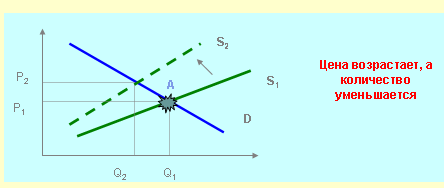
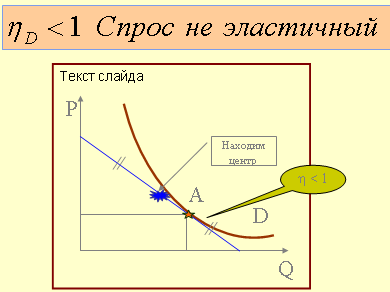
2. Если ηD < 1, при повышении цен выручка возрастет;

если ηD > 1 - выручка уменьшится.

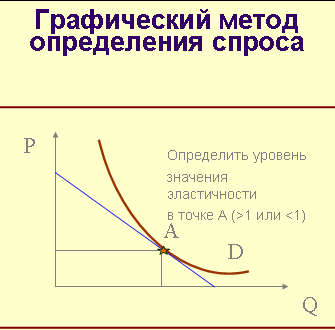
Нужно исследовать уровень эластичности спроса по цене в равновесной точке

3. Находим координаты равновесной точки А

20000-40*Q=60*Q; Q=20000/100; Q=200

P=60*Q=60*200= 12000

4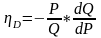 . Находим эластичность в равновесной точке

ηD=12000/(200*40)=1,5

Эластичность больше единицы, значит

Уменьшение предложения приведет к уменьшению выручки (товарооборота)

Задача № 2

Спрос и предложение рынка описываются уравнениями:

P=20000-40*Q

P=60*Q

Найти изменения равновесной точки, если государство установит налог

100 руб. с одной единицы выпуска

Решение:

1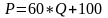 . Последствия налога графически могут быть выражены

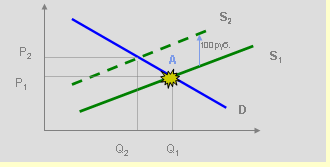
2. Находим равновесную точку до налогообложения

20000-40*Q=60*Q; Q=20000/100; Q=200

P=60*Q=60*200= 12000

3. Находим равновесную точку после налогообложения

20000-40*Q=60*Q+100; Q=(20000-100)/(100); Q=199

P=60*Q+100=60*199+100= 12040

4. Цена возросла на 40 руб., количество - на

1 единицу

Задача № 3

Спрос и предложение рынка описываются уравнениями:

P=20000-40*Q

P=60*Q

Найти изменения равновесной точки, если спрос возрастет на 10%

Решение:

1. Графическая иллюстрация изменения спроса

2. Преобразуем заданную зависимость спроса

P=20000-40*Q

Q=(20000-P)/40 Преобразованный спрос до увеличения

Новый спрос больше на 10%

Q110%=1,1*(20000-P)/40 или

Р=20000-40/1,1*Q

3. Находим равновесную точку до налогообложения

20000-40*Q=60*Q; Q=20000/100; Q=200

P=60*Q=60*200= 12000

4. Находим равновесную точку после изменения спроса

20000-40/1,1*Q=60*Q

Q=20000/96.36; Q=207.55

P=60*Q=60*207.55= 12452.83

5. Находим изменения

Количество возросло на 7,55

Цена возросла на 452,83

Задача № 4

По сравнению с прошлым годом цены на рынке листовой стали в текущем году возросли на 10%, выручка - на 5%.

Определить эластичность спроса по цене точечным способом

Решение:

1. Эластичность точечным способом определяется по формуле

2. Изменение цены задано в условии: Р/Р=0.1 (10%)

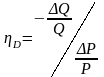
3. Находим изменение выпуска. Для этого составляем тождество по заданному условию:

П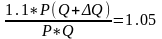 реобразуем и находим

Q/Q= - 0.05

4. Подставляем в формулу и на ходим точечную эластичность:

 D=0.05/0.1=0.5

Задача

На совещании у руководителя предприятия рассматривается проект расхода бюджета на социальные нужды 70 млн. руб. Представлены два альтернативных варианта пакетов направлений социальных расходов. Стоимость одного мероприятия по 1-му варианту 20 млн. руб., по 2-му -10 млн. руб.

Предложите решение расхода бюджета, если обсуждение проектов показало:

Вариант 1		Вариант 2
Мероприятие	Полезность	Мероприятие	Полезность
1	60	1	40
2	40	2	30
3	20	3	20
4	10	4	15
5	5	5	10
Итого	135		125

Решение

1. Оптимальная корзина мероприятий определяется условием

MU1/p1=MU2/p2

MU1, MU2 -предельные полезности мероприятий

p1, p2 - затраты на мероприятия

2. Суммарная стоимость мероприятий не должна превышать установленный бюджет 70 млн. руб.

3. Рассчитываем соотношения и выбираем оптимальную комбинацию

Вариант 1		Вариант 2
Мероприятие	MU1/p1	Мероприятие	MU2/p2
1	3	1	4
2	2**	2	3
3	1	3	2**
4	0,5	4	1,5
5	0,25	5	0,5

Затраты на выбранные мероприятия: 2*20+3*10=70млн. руб.

Задача №5

Условие:

1. Доход физического лица (I) -860 руб.

2. Потребительская корзина состоит из товаров X и Y.

3.Цена товара X (PX) – 60 руб.

4. Цена товара Y (PY) – 80 руб.

Используя нижеследующую таблицу найти оптимальную рыночную корзину.

Исходные данные

Количество Q	Предельная полезность Х MUX	Предельная полезность Y MUY
4	150	240
5	120	210
6	100	180
7	85	160
8	80	150

Р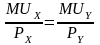 ешение:

Оптимальная корзина выбирается из:

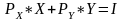
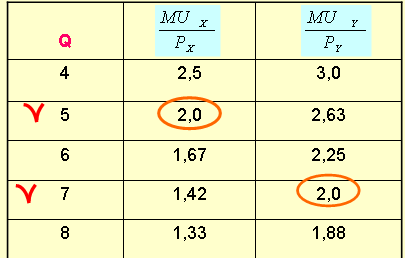
Ответ:

Количество товара X =5

Количество товара Y=7

Проверка:

(5*60 + 7*80 = 860 руб.)

Задача № 6

Условие:

1. Предельная взаимозаменяемость товара X (MEX) описывается уравнением

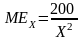
2. PX=40

3. PY=80

Найти количество товара X в рыночной корзине потребителя

Оптимальная корзина

Оптимальная корзина товаров потребителя определяется как координаты точки касания между кривой индеферентности и линией бюджета

Физическая интерпретация предельной взаимозаменяемости

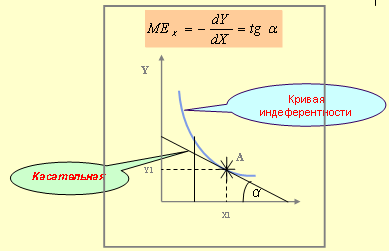
Графическая интерпретация линии бюджета

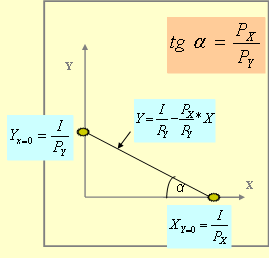
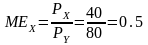
Решение:

1. Находим предельную взаимозаменяемость на основе цен

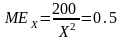
2. Находим количество товара X

Задача № 7

У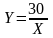 словие:

1. Изокванта предприятия описывается уравненим:

2. Предельная взаимозаменяемость ресурсов MEX=0.3

Найти количество ресурса X, потребляемого предприятием.

Р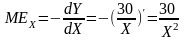 ешение:

1. Находим уравнение предельной взаимозаменяемости:

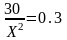
2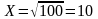 . Находим количество ресурса:

Задача № 8

Условие:

1. Средние суммарные затраты предприятия равны 20 000 руб.

2. Средние постоянные расходы – 9 000 руб.

3. Предприятие получило заказ на производство продукции по цене 12 000 руб.

Подписать договор или отказаться? Принять решение.

Оценка предложения предприятия (S=MC)

Пока Р- AVC >0 - предприятие осуществляет деятельность

Разница Р- AVC называется маржой (покрытием)

Если М= Р- AVC>=0 предприятие осуществляет деятельность

Решение:

1. Рассмотрим модель поведения в условиях чистой конкуренции.

2. Находим переменные средние затраты:

AVC=ATC-AFC=20 000 – 9 000 = 11 000 руб.

3. Находим маржу:

M=P-AVC=12 000 – 11 000 = 1 000 руб.

5. Маржа > 0.

ЗАКАЗ ПРИНИМАЕМ!

Задача № 9

Условие:

1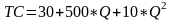 . Функция затрат предприятия описывается уравнением:

2. Цена на продукцию предприятия 3000 руб. (не зависит от объема выпуска).

Найти количество выпускаемой продукции.

Решение:

1.

2. Находим зависимость предельных затрат

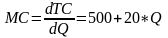
3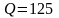 . Находим выпуск:

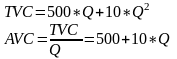
4.Находим зависимость средних переменных затрат АVC

5.Находим средние переменные затраты

АVC=500+10*125=1750

Средние затраты меньше цены, значит объем выпуска принимается!

Задача № 10

Условие:

1. Предприятие в условиях монополистической конкуренции продает свою продукцию по цене 3000 руб.

2. Функция суммарных затрат предприятия описывается уравнением:

Определить выпуск предприятия.

Модель поведения предприятия в условиях монопольной конкуренции в длительный период (LR)

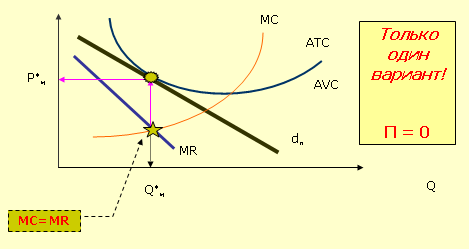
Решение:

1. Из функции затрат видно, что в задаче рассматривается длительный период.

2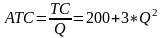 . Рассмотрим модель экономического поведения предприятия в длительный период.

3. Находим зависимость средних затрат:

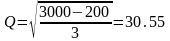
4. Находим выпуск исходя из равенства цены и средних затрат (точка Е):

Задача № 11

Условие:

1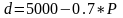 . Спрос доминирующего предприятия в условиях олигополии описывается уравнением:

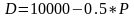
2. Спрос рынка:

3. Выпуск доминирующего предприятия составляет 250 ед.

Определить объем продаж в целом по рынку

Модель поведения предприятия в условиях олигополии на основе неявного (тайного) сговора

Решение:

1. Рассмотрим модель экономического поведения в условиях олигополии.

2. Определяем цену на рынке (цена доминирующего предприятия):

3. Определяем объем продаж в целом по рынку:

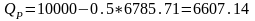
Задача № 12

Условие:

1. Цена предприятия монополиста составляет 3000 руб.

2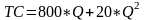 . Функция суммарных затрат:

3. Эластичность спроса по цене (η) – 3

Определить выпуск предприятия.

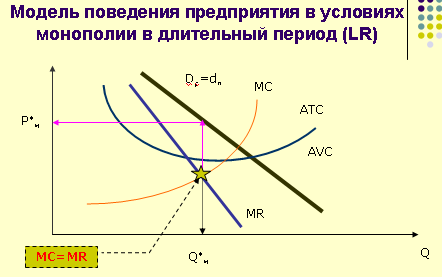
Решение:

1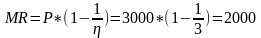 . Рассмотрим модель монополии.

2. Определяем предельный доход:

3. Определяем зависимость предельных затрат:

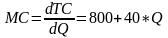
Находим выпуск (МС=МR)

Задача № 14

Условие:

1. Функция затрат монополиста характеризуется уравнением:

2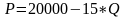 . Спрос на продукцию предприятия описывается уравнением:

Определить экономическое поведение предприятия монополиста, если он регулируется государством.

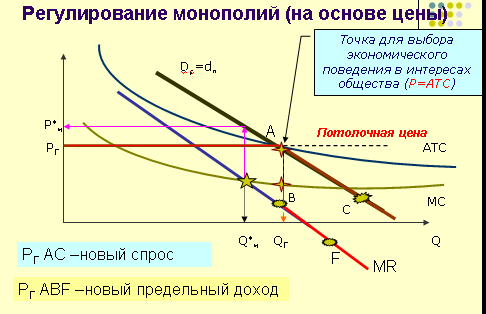
Решение:

1. Рассмотрим модель государственного регулирования.

2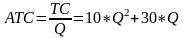 . Находим зависимость средних затрат:

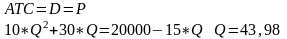3 . Находим объем выпуска:

4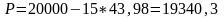 . Находим цену:

Задача № 2

П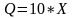 роизводственная функция описывается уравнением:

Ф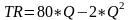 ункция дохода предприятия описывается уравнением:

Цена ресурса Х 10000 руб

Определить объем закупки ресурса Х

1. Преобразуем функцию дохода в функцию факторов:

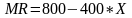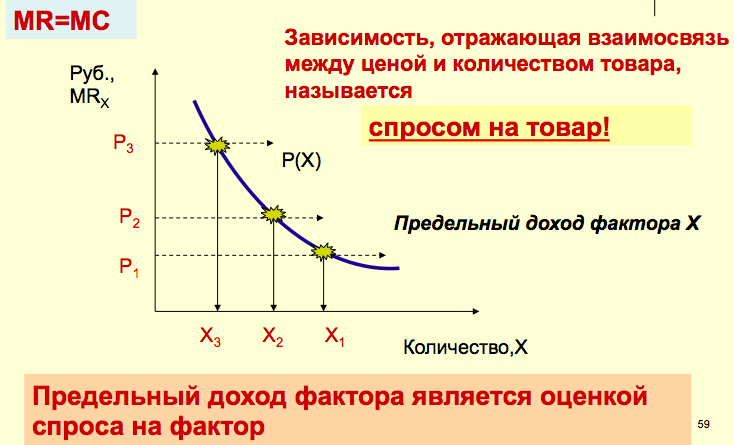
2 . Находим предельный доход фактора:

3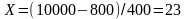 . Находим объем закупки:

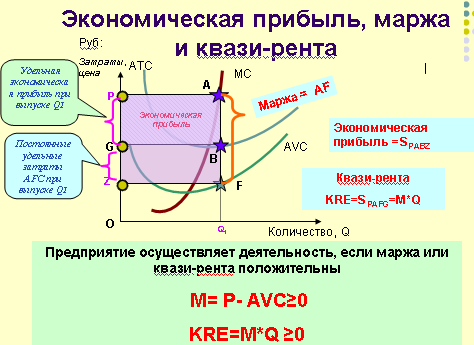
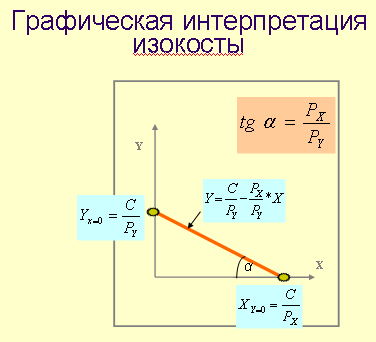
Задача №15

На рис. представлены изокванта и изокоста оптимального использования ресурсов Х и Y в производстве. Изокванта для металлургического предприятия описывается уравнением:

Y=500000-X

где Y и X - экономические ресурсы, т

По технологическим причинам использование ресурса Y не может быть ниже 350000 т, а ресурса Х - не ниже 100000 т. Сумма затрат не ограничивается.

Определить оптимальную рыночную корзину ресурсов.

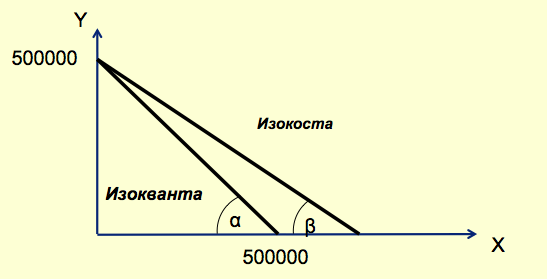
Из изокосты следует, что товар Х дешевле товара Y. Выгоднее как можно больше использовать товар Х. (Pх/Py≤1)

Поэтому расход ресурса Y принимаем на минимально возможном уровне, т.е.расход ресурса Y=350 000 т, тогда расход ресурса X=500 000- 350 000=150 000т.

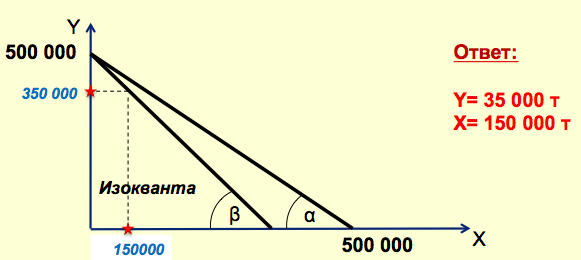
Задача № 16

Рыночная цена 1-го чел-часа в черной металлургии

100 руб/час. Зависимость дохода

предприятия от использования в производстве рабочей

силы описывается уравнением

 

где L -использование рабочей силы , млн. чел-час.

TR- доход, руб

 

Определить занятость рабочей силы на комбинате (в чел-часах)

1.Количество вовлечения ресурса в производство определяется условием

 

2. Определяем зависимость предельного дохода от рабочей силы (спрос на рабочую силу)

 

 3. Определяем использование рабочей силы58

L=25 млн. чел-час.

Оценка спроса на ресурс