
- •1.Правило Крамера для системы 2х линейных уравнений.
- •2.Определители
- •4.Вычисление определителя, приведение к треугольному виду.
- •5.Вычисление определителя методом Лапласа.
- •1.∆≠0 То система (*) имеет 1решение,которое находится по формулам:
- •15Координаты вектора
- •16Декартова прямоугольная система координат.
- •17.Сколярное произведение векторов.
- •18.Векторное произведение векторов.
- •19.Смешенное произведение векторов.
- •21.Общее ур-е прямой, нормальный вектор прямой,взаимное расположение 2х прямых.
- •23.Плоскости
- •24Нормальное ур-е плоскости
- •25.Множества, Понятие функций.
- •26.Абсолютная величина действительного числа
- •27.Основные понятия действительных чисел
- •28.Верхние и нижние границы числовых множеств.
- •29.Понятие функций и гр функций.
- •Предел последовательности
- •31.Символика
- •32.Понятие последовательности и её пределы.
- •34.Бесконечно малые и бесконечно большие послед-ти.
- •35.Монотонные послед-ти
- •Предел и непрерывность функций
- •36.Определение предела функций
- •37.Арифметические операции с пределами функций
- •38.Односторонние пределы
- •39.Бесконечно малые и бесконечно большие величины
- •40.Непрерывность функции
- •41.Односторонняя непрерывность
- •42.Точки разрыва
- •Дифференцирование одного переменного
- •44.Определение производных
- •45.Геометрический смысл производной
- •46.Дифференцирование функций
- •47Дифференциал.
- •48Дифференциалы высших порядков
- •49.Дифференцирование ф-ции заданной параметрически.
- •50.Основные теоремы диф-ого исчисления
- •51.Правило Лапиталя
- •52Формула Тейлора
- •53.Условия монотонности функции
- •54Экстремумы функции
- •55.Выпуклые и вогнутые кривые
- •56.Асимптоты гр функции
51.Правило Лапиталя
Раскрытие
неопределённости( )
)
1.f(x),g(x) определены и диф-мы в окрестности т.а за искл МБ самой т.а,причём g’(х)≠0
2. = =0
3.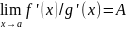 сущ-ет,тогда.
сущ-ет,тогда.
Док-во:Пусть а-конечное число,то определим знач ф-ий f(x),g(x) в т.а,а именно f(а),g(а)=0,это позволяет сделать 2усл т.
Т.х
из окрестности т.а такую, что на
 выполняются
все усл теоремы,тогда сущ-ет т.Ѯ
(а,х),
такая что собл усл т.Коши
выполняются
все усл теоремы,тогда сущ-ет т.Ѯ
(а,х),
такая что собл усл т.Коши
 =
;
=
;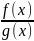 =
;
х→а при этом Ѯ→а,тогда
=
;
х→а при этом Ѯ→а,тогда
 =
= =А,
аналогично берём промежуток
=А,
аналогично берём промежуток
 на
котором вып-ся все усл теоремы, тогда
сущ-ет Ѯ
(х,а)
такая что
на
котором вып-ся все усл теоремы, тогда
сущ-ет Ѯ
(х,а)
такая что
 =
;
=
; =А,отсуда
можем утв, что
=А,отсуда
можем утв, что
 =
=
Утв теор выполняется если а- не собственное число
Аналогично
раскрывается неопр ( )
)
Пр1 =(
)=
=(
)= =1
=1
Пр2. =(
)=
=(
)= =(
)=
=(
)=
(0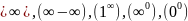 свести
к стандартным
свести
к стандартным
Пр1. =(0
=(0 =
= =(
)=
=(
)= =
=
 =0
=0
Пр2. =
= =
= =(
)=
=(
)= =
=
Пр3. =
= =
= =
= =-
=- =(
)
=
=(
)
= =0
=0
52Формула Тейлора
f(x)беск
число раз диф-ма в окрестности т
,то
для любого числа х этой окрестности и
любого нат числа справедлива
ф.Тейлора:f(x)=f(
)+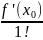 (x-
)+
(x-
)+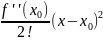 +…+
+…+ +o(
+o( )
)
если
 ,то
получим фМаклорена: f(x)=f(0)+
,то
получим фМаклорена: f(x)=f(0)+ x+
x+ +…+
+…+ +o(
+o( )
)
1. +
+
2. +o(
+o( )
)
3. +o(
+o( )
)
4.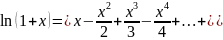 +o(
+o( )
)
5. =1+
x+
=1+
x+ +…+
+…+ +o(
+o(
6. =1+x+
=1+x+ +o(
+o(
7.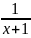 =1-x+
=1-x+ +o(
+o(
Разложения
6,7 получаются из разл 5 при

53.Условия монотонности функции
Теор.Условия монотонности функции
f:
(a,b)→𝑅
диф-ма на

УтвА.Если
 >0
на (а,в) то
>0
на (а,в) то
 возр на (а,в)
возр на (а,в)
УтвБ.Если <0 на (а,в) то убыв на (а,в)
УтвВ.Если ≡0 на (а,в) то -постоянная ф-я
Док-во:
Пусть
 любые
2 точки (а,в) причем
любые
2 точки (а,в) причем

На
 непрерывна
и диф-ма
непрерывна
и диф-ма прим
ф.Лагранжа, то сущ-ет т.Ѯ
(
)
f(
прим
ф.Лагранжа, то сущ-ет т.Ѯ
(
)
f( =
=
Если
>0,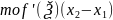 >0,
f(
>0,
f(
Если
>0,
<0,тогда
f(
Если
≡0,
=0,тогда
f(
54Экстремумы функции
Опр1.Пусть задана f: (a,b)→𝑅
УтвА.Будем
говорить,что
имеет
локальный максимум в т. (а,в)
если сущ-ет такая
(а,в)
если сущ-ет такая
 -окрестность
т.
,
что для всех х≠
из
этой окрестности,то вып f(
-окрестность
т.
,
что для всех х≠
из
этой окрестности,то вып f(
(
УтвБ.
Будем говорить,что
имеет
локальный минимум в т.
(а,в)
если ( Локальные макс и мин объединяются
под общим назв экстремум
Локальные макс и мин объединяются
под общим назв экстремум
Опр2.
Пусть задана f:
(a,b)→𝑅
если в
 (а,в)выполн
усл
(а,в)выполн
усл
 ,то
,то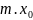 наз стационарной.
наз стационарной.
Если
в
 или не сущ-ет, то т
или не сущ-ет, то т наз критической
наз критической
Теор:Необходимое усл экстремума.
Пусть задана f: (a,b)→𝑅 если t(x) имеет в т. (а,в)локальный макс или лок минимум,то критическая т.
Док-во
1)Пусть
в т.
сущ-ет
 .Предположим
для определённости,что в т.
ф имеет локальный макс → (
.Предположим
для определённости,что в т.
ф имеет локальный макс → (
Если
х<
то
 >0;
>0; =
=
Если
х>
то
<0; =
=

 Т.о
Т.о
 и
и

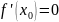

 2)Пр.
2)Пр. и
и

1-лок макс;0-лок мин;0-крит т.
Теор:1достаточное усл экстремума
Пусть f: (a,b)→𝑅удовл усл:
1. непрерывна на (а,в)
2. (х)
сущ-ет всюду на (а,в) за искл МБ т.
,тогда
1)если
(х)>0
при х<
и
(х)<0
при х>
то
-т.
макс
(х)
сущ-ет всюду на (а,в) за искл МБ т.
,тогда
1)если
(х)>0
при х<
и
(х)<0
при х>
то
-т.
макс
2) если (х)<0 при х< и (х)>0 при х> то -т.min
Т.о если при переходе через т. слева на право производная меняет знак с + на -, то -т. макс, а если с – на + то -т.min
Теор: 2достаточное усл экстремума
Пусть
для f:
(a,b)→𝑅
в т.
(а,в)
, ≠0,
тогда при
≠0
в т
ф имеет макс, а при
≠0
в т
имеет min
≠0,
тогда при
≠0
в т
ф имеет макс, а при
≠0
в т
имеет min


55.Выпуклые и вогнутые кривые
Опр1.Непрерывная
кривая у=
наз выпуклой вверх(вниз) на
если любая дуга этой кривой,соед т.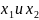 такие, что а
такие, что а лежат выше(ниже) стягивающей её хорды
лежат выше(ниже) стягивающей её хорды
Опр2.Кривая у= наз гладкой на если её задание имеет непрерывную на (а,в) производную (х)
Геом:нигде нет угловых точек
Теор:1усл выпуклости функции: у=
1)Выпуклая вниз на если её произв (х) возр на
 2)Выпуклая
вверх на
если её произв
(х)
убыв на
2)Выпуклая
вверх на
если её произв
(х)
убыв на







Теор:2усл выпуклости функции
Пусть
для f:
[a,b]→𝑅
всюду на (а,в) сущ-ет
 ,тогда
кривая у=
выпуклая вниз на [a,b]
если всюду
,тогда
кривая у=
выпуклая вниз на [a,b]
если всюду
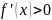 и выпуклая вверх на [a,b]
если всюду
и выпуклая вверх на [a,b]
если всюду

Док-во
Если
>0
на (а,в) то
 возраст,тогда
по т.1 у=
выпуклая вниз на [а,в]. Если
<0
на (а,в) то
убыв
,тогда по т.1 у=
выпуклая вверх на [а,в]
возраст,тогда
по т.1 у=
выпуклая вниз на [а,в]. Если
<0
на (а,в) то
убыв
,тогда по т.1 у=
выпуклая вверх на [а,в]
Опр3
т.М(
; )
наз т.перегиба кривой у=
если
она отделяет участок выпуклости вверх
от уч.выпуклости вниз
)
наз т.перегиба кривой у=
если
она отделяет участок выпуклости вверх
от уч.выпуклости вниз
Теор.Необх. и достаточное усл для т.перегиба
Пусть для f: [a,b]→𝑅 сущ-ет для того чтобы т. была т.перегиба кривой у=
А)необх: =0
Б)при
переходе через
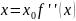 меняла
знак
меняла
знак
 Зам:гладкую
кривую наз вогнутой вверх(вниз) на
[а,в]если она лежит выше(ниже) любой
касательной,проведённой в т. с абсциссами
х
(а,в)
Зам:гладкую
кривую наз вогнутой вверх(вниз) на
[а,в]если она лежит выше(ниже) любой
касательной,проведённой в т. с абсциссами
х
(а,в)



