
- •1.Правило Крамера для системы 2х линейных уравнений.
- •2.Определители
- •4.Вычисление определителя, приведение к треугольному виду.
- •5.Вычисление определителя методом Лапласа.
- •1.∆≠0 То система (*) имеет 1решение,которое находится по формулам:
- •15Координаты вектора
- •16Декартова прямоугольная система координат.
- •17.Сколярное произведение векторов.
- •18.Векторное произведение векторов.
- •19.Смешенное произведение векторов.
- •21.Общее ур-е прямой, нормальный вектор прямой,взаимное расположение 2х прямых.
- •23.Плоскости
- •24Нормальное ур-е плоскости
- •25.Множества, Понятие функций.
- •26.Абсолютная величина действительного числа
- •27.Основные понятия действительных чисел
- •28.Верхние и нижние границы числовых множеств.
- •29.Понятие функций и гр функций.
- •Предел последовательности
- •31.Символика
- •32.Понятие последовательности и её пределы.
- •34.Бесконечно малые и бесконечно большие послед-ти.
- •35.Монотонные послед-ти
- •Предел и непрерывность функций
- •36.Определение предела функций
- •37.Арифметические операции с пределами функций
- •38.Односторонние пределы
- •39.Бесконечно малые и бесконечно большие величины
- •40.Непрерывность функции
- •41.Односторонняя непрерывность
- •42.Точки разрыва
- •Дифференцирование одного переменного
- •44.Определение производных
- •45.Геометрический смысл производной
- •46.Дифференцирование функций
- •47Дифференциал.
- •48Дифференциалы высших порядков
- •49.Дифференцирование ф-ции заданной параметрически.
- •50.Основные теоремы диф-ого исчисления
- •51.Правило Лапиталя
- •52Формула Тейлора
- •53.Условия монотонности функции
- •54Экстремумы функции
- •55.Выпуклые и вогнутые кривые
- •56.Асимптоты гр функции
42.Точки разрыва
1) разрывна в т. если она не явл. непрерывной в этой т.
2)Если
разрывна
в т.
и если сущ-ет конечное знач-ие
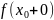 и
и
 ,
то говорят, что
имеет в
разрыв
1рода,в
противном случае он наз разрывом
2 рода.
,
то говорят, что
имеет в
разрыв
1рода,в
противном случае он наз разрывом
2 рода.
Разновидности разрыва 1 рода


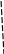
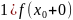 ≠
разрыв
типа конечного скачка
≠
разрыв
типа конечного скачка
Скачёк ф= -
2) = ≠ устранимый разрыв
Устранение разрыва: значение ф в т. полагаем=lim
Разновидности разрывов 2рода
1)один
из пределов бесконечный
=
или
 или
или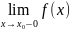 =
бесконечный разрыв
=
бесконечный разрыв
2)Хотя бы один из односторонних пределов не сущ-ет
у= чем ближе к 0 тем чаще колебания
чем ближе к 0 тем чаще колебания
в 0 значения не определено
Пр1 у=arctg1/x
Ф непрерывна во всех т кроме 0
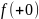 =
= =
=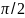
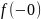 =
=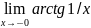 =
=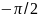
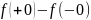 =
=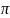 -скачёк
ф
-скачёк
ф
Пр2 ф-я «антье от х» у=
В
т.х=К К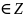
f(K+0)= =К
=К =f(K)
=f(K)
разрыв 1рода
 Пр3
у=1/х-1
Пр3
у=1/х-1
Ф непрерывна во всех т кроме 1
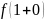 =
= =+
=+
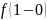 =
=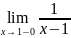 =-
=-
разрыв 2 рода
43.Св-ва непрерывных функций
1 теорема Вейерштрасса
Если f: [a,b]→𝑅 непрерывна на [a,b],то она ограниченна
2 теорема Вейерштрасса
Если f: [a,b]→𝑅 непрерывна на [a,b],то она достягает на этом сегменте своего наим и наиб значения.
1теорема Коши для непрерывных функций
Пусть
f:
[a,b]→𝑅
непрерывна на [a,b]
и принимает на концах сегмента значения
разных знаков.Это означает, что
f(a)f(b)<0,тогда
сущ-ет т.С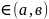 такая
что f(с)=0
такая
что f(с)=0
Такая кривая пересечёт ось х хотя бы в одной т.
2теорема Коши для непрерывных функций
Пусть f: [a,b]→𝑅 непрерывна на [a,b] и на его концах принимает неравные значения f(a)=А; f(в)=В
Пусть С-л.ч. заключённое между А и В тогда на [a,b]найдётся т.С, такая что f(с)=С др словами непрерывная ф-я при переходе от одного человека к др принимает все промежуточные значения
f(a)<C< f(в)
сущ-ет т.С, что f(с)=С
с
Дифференцирование одного переменного
44.Определение производных
Опр. f: (a,b)→𝑅 ф действительного переменного
Взяв
произвольную т.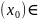 (а,в)
составим отн:
(а,в)
составим отн:
 где
а<x<b,x≠
где
а<x<b,x≠
УтвА.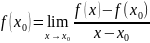 наз
производным
наз
производным
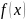 в т.
в т.
УтвБ.
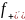 (
(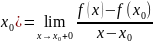 наз
провосторонней произв
наз
провосторонней произв
УтвВ. (
(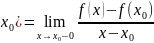 наз
левосторонней произв
наз
левосторонней произв
УтвГ.если
один из пределов А,Б,В=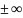 ,то
соотв производная наз бесконечной
произв.
,то
соотв производная наз бесконечной
произв.
УтвД.если f: [a,b]→𝑅 то в конечных т. [a,b]необх и достаточно чтобы сущ-али равные односторонние произв в т.
(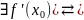 (
(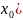 ):
(
):
(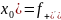 (
(
Пр1f(x)=
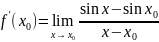 =
=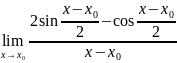 =
=
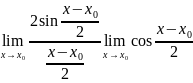 =
=
Пр2.f(x)=│ x=1
x=2
x=1
x=2
(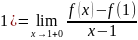 =
=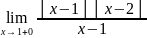 =
=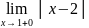 (
(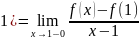 =
-
=
-
(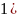 ≠
(
произв
не сущ-ет
(
≠
(
произв
не сущ-ет
(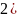 ≠
(
произв
не сущ-ет
≠
(
произв
не сущ-ет
Пр3.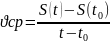 если
если
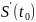 сущ-ет,то
сущ-ет,то
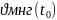 =
=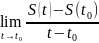
Зам-ие:∆х=х- , ∆f( =f(x)-f( )=f( +∆x)-f( ,тогд опр произв:
f(
=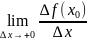 ,
(
=
,
(
=
,
(
=
,
(
=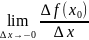
45.Геометрический смысл производной
 Опр1.Кривая
l
наз ориентированной кривой если на ней
задан обход. Если при обходе т.М следует
за т.
,то
будем говорить,что М нах справа от
.Если
при обходе т.М предшествует т.
,
то будем говорить,что м нах слева.Если
кривая в явном виде у(х), то напр обхода
задаётся направлением возрастания х
Опр1.Кривая
l
наз ориентированной кривой если на ней
задан обход. Если при обходе т.М следует
за т.
,то
будем говорить,что М нах справа от
.Если
при обходе т.М предшествует т.
,
то будем говорить,что м нах слева.Если
кривая в явном виде у(х), то напр обхода
задаётся направлением возрастания х
Если
кривая задана параметрически
 ,то
напр обхода задеется возрастанием t
,то
напр обхода задеется возрастанием t
Опр2.Пусть
 -любая
т ориентированная кривой l,лежащая
справа от т
и
-любая
т ориентированная кривой l,лежащая
справа от т
и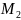 -любая
т ориентированная кривой l,лежащая
слева от М
-любая
т ориентированная кривой l,лежащая
слева от М

 Рассмотрим
секущие
Рассмотрим
секущие
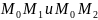

УтвА.Правосторонней
касательной l
в т
наз предельное положение секущей
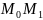 ,когда
т
стремиться
вдоль по кривой к т
,оставаясь
справа от т
,когда
т
стремиться
вдоль по кривой к т
,оставаясь
справа от т
УтвБ.Левовосторонней
касательной l
в т
наз предельное положение секущей
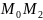 ,когда
т
стремиться
вдоль по кривой к т
,оставаясь
слева от т
,когда
т
стремиться
вдоль по кривой к т
,оставаясь
слева от т
УтвВ.Если левостороннее и правостороннее касание в т совп, то такая прямая наз касательной (l)в т
УтвГ.Если левостороннее и правостороннее касание в т не совп, то наз угловой т.
Пусть
f:
(a,b)→𝑅
,в т (а,в)сущ-ет
(а,в)сущ-ет
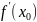 ,тогда:tg
,тогда:tg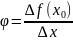 ,
∆x→0,то
секущая становится касательной,то tg
,
∆x→0,то
секущая становится касательной,то tg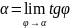 =
=





Производная ф в точке-это tg угла наклона касательной в т
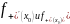 -это
tg
угла наклона правосторонней и левосторонней
⦟касания.
-это
tg
угла наклона правосторонней и левосторонней
⦟касания.
Если
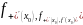 бесконечные произв, то соотв касательные
║
оси ОУ
бесконечные произв, то соотв касательные
║
оси ОУ
У=f( =K(x- )ур-е прямой,проходящей через т.
К=
у=f( )+ (x- )ур-е касательной,проходящей через т
Опр3.Прямая линия ┴к касательной в т( ,f( )) и проходящая через т. наз нормалью кривой у= f( ) в т( ,f( ))
,тогда
если
=0,ур-е
нормали зап: у= f(
)=
