4. Определения и примеры
Рассмотрим
какую-нибудь область 
в 
(на
прямой, на плоскости, в пространстве).
Предположим, что «мера»
(длина,
площадь, объем, соответственно) конечна.
Пусть случайный эксперимент состоит в
том, что мы наудачу бросаем в эту область
точку. Термин «наудачу» означает,
что вероятность попадания точки в любую
часть 
не
зависит от формы или расположения
внутри
.
Определение 9.
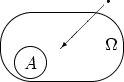Эксперимент
удовлетворяет условиям «геометрического
определения вероятности», если
его исходы можно изобразить точками
некоторой области
в
так,
что вероятность попадания точки в любую
часть
не
зависит от формы или расположения
внутри
,
а зависит лишь от меры области
и,
следовательно (понять,
почему),
пропорциональна этой мере:
где 
обозначает
меру области
(длину,
площадь, объем и т.д.).
Если для точки, брошенной в область , выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области .
Пример 7. Точка наудачу бросается на отрезок [0, 1]. Вероятность ей попасть в точку 0,5 равна нулю, так как равна нулю мера множества, состоящего из одной точки («длина точки»). Но попадание в точку 0,5 не является невозможным событием — это один из элементарных исходов эксперимента. Общее число элементарных исходов здесь бесконечно, но все они по-прежнему «равновозможны» — уже не в смысле классического определения вероятности, применить которое здесь нельзя из-за бесконечности числа исходов, а в смысле определения 9.
Задача о встрече
Пример
8. Два
лица 
и 
условились
встретиться в определённом месте между
двумя и тремя часами дня. Пришедший
первым ждет другого в течение 10 минут,
после чего уходит. Чему равна вероятность
встречи этих лиц, если каждый из них
может прийти в любое время в течение
указанного часа независимо от другого?
Решение. Будем
считать интервал с 14 до 15 часов отрезком
[0, 1] длиной в 1 час. Пусть 
(«кси»)
и 
(«эта») —
моменты прихода
и
—
точки отрезка [0, 1]. Все возможные
результаты эксперимента — точки
квадрата со стороной 1: 
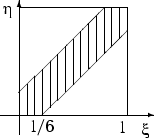
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества :
(10 минут = 1/6 часа). Попадание в множество наудачу брошенной в квадрат точки означает, что и встретятся. Тогда вероятность встречи равна
Задача Бюффона(1)
Пример
9. На
плоскости начерчены параллельные
прямые, находящиеся друг от друга на
расстоянии 
.
На плоскость наудачу брошена игла
длины 
.
Какова вероятность того, что игла
пересечёт какую-нибудь прямую?
Решение. Поймем,
что означает здесь «наудачу брошена
игла».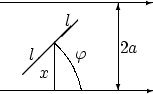 
Возможные
положения иглы (отрезка) на плоскости
полностью определяются положением
середины иглы и углом поворота иглы
относительно какого-либо направления.
Причём две эти переменные (положение
центра и угол поворота) меняются
независимо друг от друга. Обозначим
через 
расстояние
от середины иглы до ближайшей прямой,
а через 
—
угол между каким-то направлением прямых
и иглой.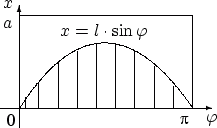 
Множество
возможных положений иглы целиком
определяется выбором наудачу точки из
прямоугольника 
.
Игла
пересекает ближайшую прямую, если
координаты выбранной наудачу точки
удовлетворяют неравенству: 
.
Площадь области
,
точки которой удовлетворяют такому
неравенству, равна
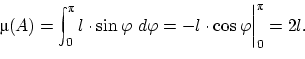
Поделим
на 
и
получим, что искомая вероятность равна 
.