6.6. Метод динамического программирования

Это метод стабилизации многошаговых процессов, основу которого составляют:

-принцип оптимальности;

-инвариантное погружение;

-функциональное уравнение, получаемое на основе принципа оптимальности и инвариантного погружения.

Основная идея метода заключается в следующем. Вместо решения исходной задачи ее включают в некоторое семейство задач оптимизации (инвариантное погружение). При этом может оказаться, что между отдельными задачами существуют простые соотношения и среди задач найдутся такие, которые легко решаются. Тогда, используя решение и соотношения, связывающие отдельные семейства, получают решение исходной задачи. Например, требуется найти минимум функции вида:

, (6.91)

где - прямое произведение областей (множеств) определения функций .

Рассмотрим семейство задач

(6.92)

В последнем соотношении

.

В (6.92) параметр m можно рассматривать как дискретное время. Введем так называемую функцию Беллмана

.

Очевидно,

.

Второе слагаемое в последнем выражении есть B_m, поэтому функция Беллмана удовлетворяет функциональному уравнению

или, в силу независимости B_m от x_m+1,

, (6.93)

причем .

Решая (6.93) с учетом последнего условия, получим и . Решением исходной задачи будут и .

Таким образом, метод динамического программирования сводит задачу минимизации скалярных функций от n переменных к n задачам минимизации скалярных функций одной переменной. В результате существенно снижается объем вычислений.

При числовом решении задачи без использования метода динамического программирования при - конечных множествах, состоящих каждая из точек, методом перебора потребовалось бы рассмотреть вариантов, а с использованием метода динамического программирования - всего вариантов.

При использовании (6.93) вычисление производится в направлении возрастания аргумента, т.е. в "прямом времени", поэтому уравнение (6.93) называют прямым уравнением Беллмана. Уравнение Беллмана в обратном времени называют обратным уравнением Беллмана.

Для получения обратного уравнения Беллмана производят инвариантное погружение исходной задачи в семейство задач:

где .

При m=1 имеем

.

Введем функцию Беллмана

.

Очевидно,

или

. (6.94)

В более сложных случаях при выводе уравнения Беллмана используется принцип оптимальности.

Принцип оптимальности

В общем случае принцип оптимальности формулируется следующим образом: оптимальная стратегия (поведение) обладает тем свойством, что, каковы бы ни были начальное состояние и решения на начальном этапе, решения на последующем этапе должны составлять оптимальную стратегию относительно состояния, которое получается в результате принятия решений на начальном этапе.

В задачах оптимального управления оптимальность определяется функционалом (критерием оптимальности) , состояние - фазовым вектором , стратегия - это управление на всем интервале , решение - это выбор управления.

Для задачи оптимизации справедлив принцип оптимальности, обладающий марковским свойством. По определению, задача оптимального управления обладает марковским свойством, если после выбора управления на интервале влияние процесса управления на оставшемся интервале величина функционала зависит только от состояния в конце начального интервала и выбора управления в последующие моменты времени, т.е. на интервале .

Для формулировки принципа оптимальности рассмотрим задачу

(6.95)

Для этой задачи справедлив принцип оптимальности, формулируемый следующим образом: для оптимальности допустимой задачи (6.95) для пары необходимо, чтобы при любом управление было оптимальным относительно состояния , в котором окажется объект в момент при использовании на начальном отрезке времени управления .

Этот принцип называется прямым принципом оптимальности и доказывается от противного.

Допустим, что утверждение неверно и существует допустимое управление , переводящее объект из точки в точку в момент времени , при котором функционал

принимает меньшее значение, чем при управлении , т.е.

.

Тогда критерий оптимальности в задаче (6.95) при управлении

принимает меньшее значение, чем при управлении , т.е.

,

а это противоречит оптимальности управления .

Принцип оптимальности для задачи оптимального управления является частным случаем следующего более общего утверждения: если допустимая для задачи (6.95) пара оптимальна, то каков бы ни был подинтервал , управление на этом подинтервале является оптимальным относительно граничных точек и .

При приведенное утверждение называют обратным принципом оптимальности. Для оптимальности, допустимой для задачи (6.95) пары , необходимо, чтобы при любом управление было оптимальным относительно конечного для интервала состояния .

Функция и уравнение Беллмана

Произведем инвариантное погружение задачи (6.95) в семейство задач, которое получается из задачи (6.95) при замене начального условия параметрическим условием . В условии рассматриваются как параметры. Исходная задача выделяется как частная при .

Минимальное значение критерия оптимальности при параметрическом начальном условии зависит от выбранных значений :

,

причем , и функция называется функцией Беллмана.

Получим уравнение Беллмана. Очевидно, для сдвига по времени получим

.

В силу принципа оптимальности

или

.

Фазовый вектор и соответственно функция Беллмана в левой части последнего соотношения не зависит от управления на интервале , поэтому в этом соотношении функцию Беллмана можно перенести в правую часть и внести под знак минимума:

.

В полученном уравнении по теореме о среднем интеграл представим в виде

; .

Разность значений функции Беллмана, используя разложение последнего слагаемого в ряд Тейлора, представим в виде (ограничившись только линейным относительно членами):

.

Разделив обе части на , устремим к нулю. Тогда, приняв , в пределе получим уравнение

(6.96)

или, учитывая, что , а также то, что , можем записать

.

Это уравнение называется уравнением Беллмана. Так как функция не зависит от управления , последнее слагаемое в правой части можно вынести за скобки, и уравнение Беллмана записать для n-мерного случая, когда

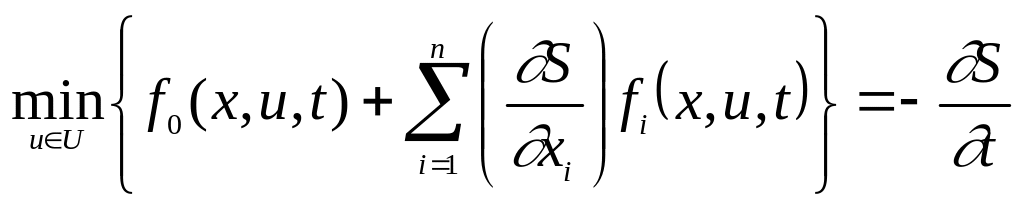
или в векторной форме

, (6.97)

где - производная скалярной функции по векторному аргументу. Итак, основной результат:

Если функция Беллмана дифференцируема, то для того, чтобы допустимая пара для задачи (6.95) была ее решением, необходимо, чтобы она удовлетворяла уравнению Беллмана (6.97) при граничном условии

. (6.98)

Если минимум в левой части (6.97) достигается во внутренних точках множества , то уравнение Беллмана можно представить в виде:

(6.99)

(6.100)

Уравнения (6.100) выражают необходимое условие минимума левой части (6.97) и заменяют опущенную в (6.99) операцию минимизации по управлению.

Если правые части уравнений объекта и подынтегральное выражение в критерии оптимальности, т.е. функции , явно не зависят от времени и конечный момент времени не фиксирован, то функция Беллмана не зависит явно от времени и .

Оптимальное управление методом динамического программирования находится следующим образом:

1) Из уравнений (6.100) определяется управление как функция от S, т.е. ;

2) Подставив в (6.99) и решив его при краевом условии (6.98), находят функцию Беллмана как функцию координат ;

3) Подставив найденную функцию Беллмана в выражение , получают оптимальное управление как функцию фазовых координат .

134