
- •6.2. Задача управления системой при фиксированных концах и времени процесса
- •6.3. Задача с подвижными концами и нефиксированным временем процесса управления
- •6.4. Задача оптимального управления при ограничениях на управление
- •6.5. Принцип максимума
- •Задача максимального быстродействия
- •Системы с переменной областью управления
- •6.6. Метод динамического программирования
Задача максимального быстродействия
Эта задача
формулируется следующим образом: найти
допустимое управление, переводящее
заданный объект из начальной точки
(множества) в конечную точку (конечное
множество) за минимальное время. Она
является частным случаем задачи с
подвижными концами и нефиксированным
временем (задача Майера). Если положить
![]() ,
то критерий оптимальности имеет вид
,
то критерий оптимальности имеет вид
![]() ,
поэтому в данном случае
,
поэтому в данном случае
![]() ,
,
![]() и функция Понтрягина
и функция Понтрягина
![]() .
Если концы закреплены, то
.
Если концы закреплены, то
![]() ,
и условия трансверсальности принимают
вид
,
и условия трансверсальности принимают
вид
![]() .
.
Рассмотрим задачу максимального быстродействия, когда объект описывается линейными дифференциальными уравнениями:
 (6.62)
(6.62)
Эта задача называется линейной задачей максимального быстродействия.
В матричной форме уравнения объекта имеют вид
![]() .
.
Предполагается,
что эти уравнения являются уравнениями
в отклонениях, поэтому конечное состояние,
в которое нужно перевести объект, есть
начало координат
![]() .
.
Функция Понтрягина
 ,
,
где
![]() подчиняется сопряженному уравнению
подчиняется сопряженному уравнению
![]()
или сопряженной системе уравнений
![]() .
.
Согласно принципу максимума, оптимальное управление находят из условия
![]()
или
 ,
,
где
![]() .
.
Если выполняются
так называемые условия нормальности,
то сумма
![]() обращается в нуль только в изолированных
точках. В этом случае из последнего
тождества следует, что координаты
обращается в нуль только в изолированных
точках. В этом случае из последнего
тождества следует, что координаты
![]() оптимального управления
оптимального управления
![]() кусочно-постоянны и принимают крайние
значения
кусочно-постоянны и принимают крайние
значения
![]() или
или
![]() :
:

В частном случае,
когда ограничение имеет вид
![]()
![]() .
.
Условие нормальности.
Введем в рассмотрение (![]() )
матрицы
)
матрицы
![]() ,
,
где
![]() - j-е столбцы матриц B,AB,...,An-1B
.
- j-е столбцы матриц B,AB,...,An-1B
.
Для объекта
выполнено условие нормальности или
условие общности положения, если
матрицы
![]() (при
(при
![]() )
невырождены, т.е. их столбцы линейно
независимы, или det
(при j=1,...,r). Объект в этом случае
называется нормальным.
)
невырождены, т.е. их столбцы линейно
независимы, или det
(при j=1,...,r). Объект в этом случае
называется нормальным.
Для объекта
![]()
условие нормальности всегда выполнено.
Теорема об n интервалах. Если в линейной задаче максимального быстродействия объект является нормальным, и его характеристическое уравнение
![]()
имеет
только действительные корни, то
оптимальные управления
![]() кусочно-постоянны, они принимают только
крайние значения и имеют не более
кусочно-постоянны, они принимают только
крайние значения и имеют не более
![]() интервалов постоянства, т.е. не более
интервалов постоянства, т.е. не более
![]() переключений.
переключений.
Если характеристическое уравнение имеет комплексные корни, то число переключений зависит от начальных условий. Оно может быть сколь угодно большим, но конечным.
Пример 6.9. Определить оптимальное по быстродействию управление объектом, уравнения динамики которого в относительных единицах имеют вид
![]()
Решение. Преобразуем уравнение объекта к форме уравнений состояния:
![]() .
.
Для данной линейной системы проанализируем выполнение условия нормальности. Из уравнений состояния видно, что
![]() ,
,
![]() ,
,
а
следовательно, для матрицы
![]() получим выражения
получим выражения
![]()
и
очевидно, что
![]() и система нормальна. Это, кстати, следует
из самого условия, где система представлена
линейным уравнением второго порядка.
и система нормальна. Это, кстати, следует
из самого условия, где система представлена
линейным уравнением второго порядка.
Решим вопрос о применении теоремы об интервалах для данной системы.
![]() ,
,
![]() .
.
Корни характеристического уравнения мнимые, а следовательно, теорему об интервалах применять нельзя. Рассмотрим, однако, систему с целью оценить характер полученного управления.
Составим функцию Гамильтона
![]() .
.
Оптимальное управление находим из условия максимума H:
![]() .
.
Для отыскания оптимального уравнения составим и решим управление Эйлера-Лагранжа
![]() .
.
Полученную систему дифференциальных уравнений решим, как и в предыдущем случае, сведением к одному уравнению второго порядка
![]() ,
,
характеристическое
уравнение которого имеет мнимые корни
![]() ,
которым соответствует общее решение
вида
,
которым соответствует общее решение
вида
![]() ,
,
где
константы
![]() или, что то же самое,
или, что то же самое,
![]() определяются начальными значениями
определяются начальными значениями
![]() и
и
![]() ,
а
,
а
![]() выражается из уравнений Эйлера-Лагранжа:
выражается из уравнений Эйлера-Лагранжа:
![]() .
.
Таким образом, оптимальное управление принимает вид

Теперь очевидно,
что переключения будут происходить в
точках
![]() ,
,
![]() ,
,
![]() ,
пока не будет достигнуто начало координат.
,
пока не будет достигнуто начало координат.
Дальнейшее исследование с оценкой фазовых траекторий и точек переключения обсуждается в задаче 7.5 следующего раздела.
Пример 6.10. Для системы

найти
уравнение
![]() ,
переводящее её из состояния
,
переводящее её из состояния
![]() в начало координат
в начало координат
![]() за минимальное время, т.е.
за минимальное время, т.е.
![]() .
.
Решение. Поскольку это задача на максимальное быстродействие, то проанализируем систему на нормальность. Из условия очевидно, что:
 ,
,
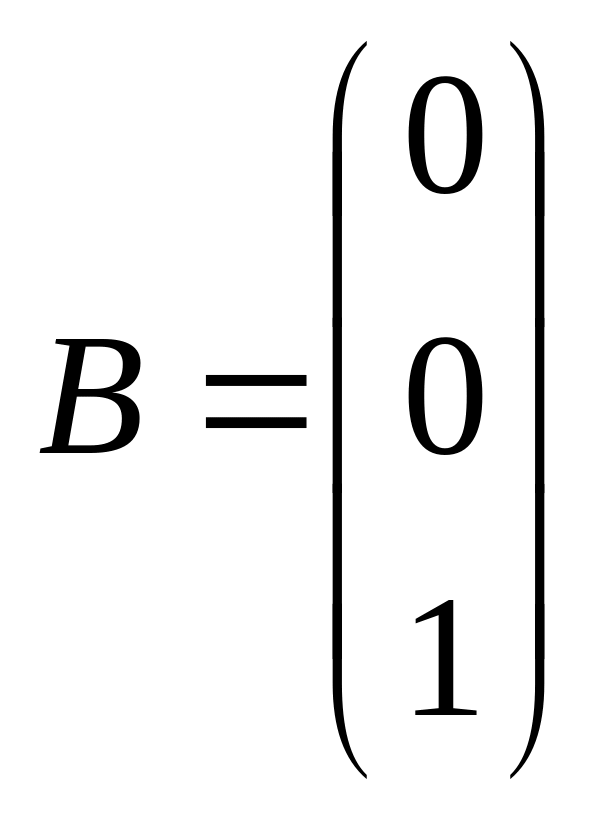 ,
,
а следовательно,
 .
.
Таким образом, система нормальна.
Найдём собственные числа матрицы А:
 .
.
Поскольку
все собственные числа действительные,
то к системе можно применить теорему
об интервалах, из которой следует, что
число переключений не должно превысить
размерности задачи минус один (т.е. не
более двух, т.к. в нашем случае
![]() ).
).
Для решения задачи составим гамильтониан
![]() ,
,
соответствующие уравнения Эйлера-Лагранжа и их решения:

Из структуры гамильтониана и принципа максимума следует, что:
![]() .
.
Таким образом,
очевидно, что
![]() ,
а знак определяется знаком квадратной
функции
,
а знак определяется знаком квадратной
функции
![]() ,
которая может иметь две, одну и ни одной
точки, где она обращается в нуль (см.
рис. 6.8).
,
которая может иметь две, одну и ни одной
точки, где она обращается в нуль (см.
рис. 6.8).

Рис. 6.8. Возможные варианты поведения функции
Очевидно, что если
начинать процесс с
![]() ,
то это не может дать оптимального
результата, поскольку в этом случае
начальное движение будет направлено в
сторону от начала координат. Следовательно,
варианты 1, 2, 3 (см. рис. 6.8) отпадают. Случаи
5 и 6, которые соответствуют
,
то это не может дать оптимального
результата, поскольку в этом случае
начальное движение будет направлено в
сторону от начала координат. Следовательно,
варианты 1, 2, 3 (см. рис. 6.8) отпадают. Случаи
5 и 6, которые соответствуют
![]() для
для
![]() ,
не обеспечат достижения
.
Таким образом, характер изменения
для некоторого процесса управления
имеет следующий вид:
,
не обеспечат достижения
.
Таким образом, характер изменения
для некоторого процесса управления
имеет следующий вид:
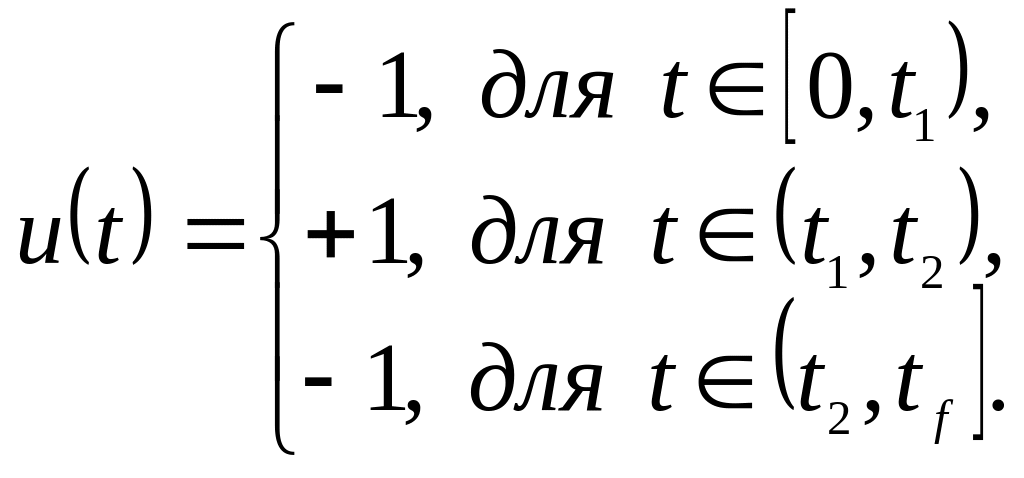
Подставим последовательно в уравнение движения системы и, используя начальные и конечные условия и условия непрерывности координат в точках переключения, получим:

![]()

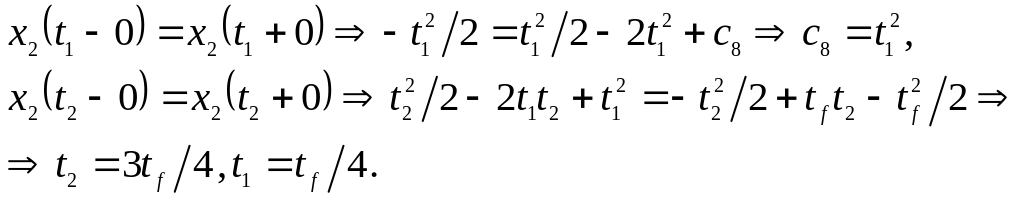


Подставляя в
последнее равенство выражения для
![]() и
и
![]() ,
получим минимальное время достижения
начала координат
,
получим минимальное время достижения
начала координат
![]() ,
а
,
а
![]() ,
,
![]() .
.
Таким образом, нами определены три интеграла знакопостоянства и элементы переключения и уравнения для фазовых координат.
Изменим задачу,
положив, что
![]() - свободно. Но тогда, из условия
трансверсальности
- свободно. Но тогда, из условия
трансверсальности
![]() следует, что
следует, что
![]() (см. начало решения задачи), и, кроме
того,
(см. начало решения задачи), и, кроме
того,
![]() .
.
Если найти корни уравнения , получим
![]() ,
,
![]() .
.
Если
![]() ,
то
,
то
![]() ,
если же
,
если же
![]() ,
то
,
то
![]() .
Таким образом, остаётся только одна
точка переключения, и мы можем для
управления записать:
.
Таким образом, остаётся только одна
точка переключения, и мы можем для
управления записать:
![]()
Далее для фазовых координат получим:
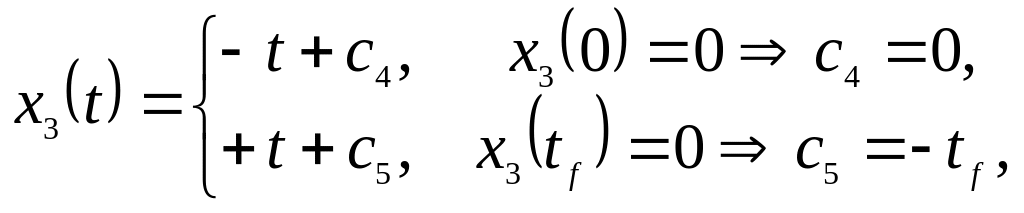
![]() .
.
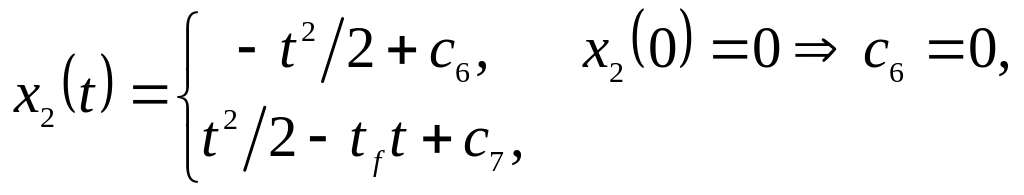
![]() .
.


Решение получено, и отметим, что с освобождением одной из координат число переключений уменьшилось на единицу.
Освободим теперь
в условии и
![]() .
Тогда дополнительно возникает второе
условие трансверсальности
.
Тогда дополнительно возникает второе
условие трансверсальности
![]() ,
которое принимает вид
,
которое принимает вид
![]() ,
,
что
приводит к следующему виду функции
![]() :
:
![]() .
.
Из последнего следует, что знакопостоянна, а это значит, что для и переключений управления нет.
Тогда
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
а из условия получаем
![]() .
.
