6.4. Задача оптимального управления при ограничениях на управление
Достаточно часто
при анализе реальных систем различной
природы (в технике, экономике, экологии
и т.п.) на управляющее воздействие
накладываются естественные ограничения
в виде неравенств:
 . (6.24)
. (6.24)
Ограничения
вида (6.24) с помощью замены

приводим
к стандартному виду
 .
.
Тогда
решим следующую задачу с фиксированными
концами: перевести систему, эволюция
которой описывается векторным уравнением
 , (6.25)
, (6.25)
где
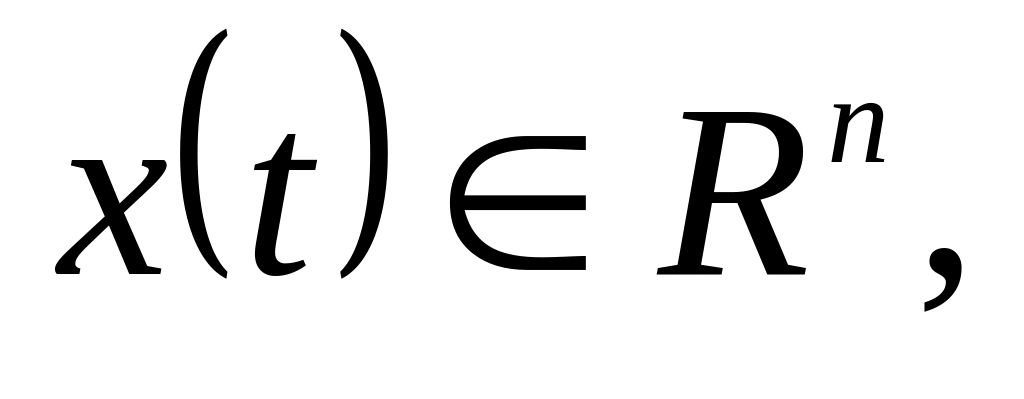 из начальной точки
из начальной точки
 в конечную
в конечную
 ,
минимизируя функционал
,
минимизируя функционал
 ,
(6.26)
,
(6.26)
при
условии, что на вектор управлений u(t),
где
 наложены
ограничения:
наложены
ограничения:
 (6.27)
(6.27)
Чтобы
от допустимой замкнутой для управления
области (6.26) или (6.27) перейти к открытой,
введем дополнительные переменные в
виде вектора
 такого, что
такого, что
 . (6.28)
. (6.28)
Сформулированная
задача представляет собой задачу
Лагранжа
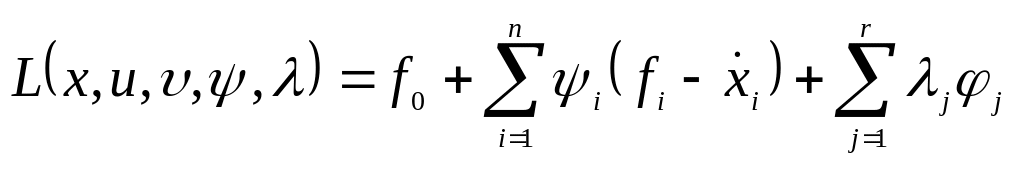
или
в векторной форме
 . (6.29)
. (6.29)
Решение поставленной
задачи определим из уравнений
Эйлера-Лагранжа
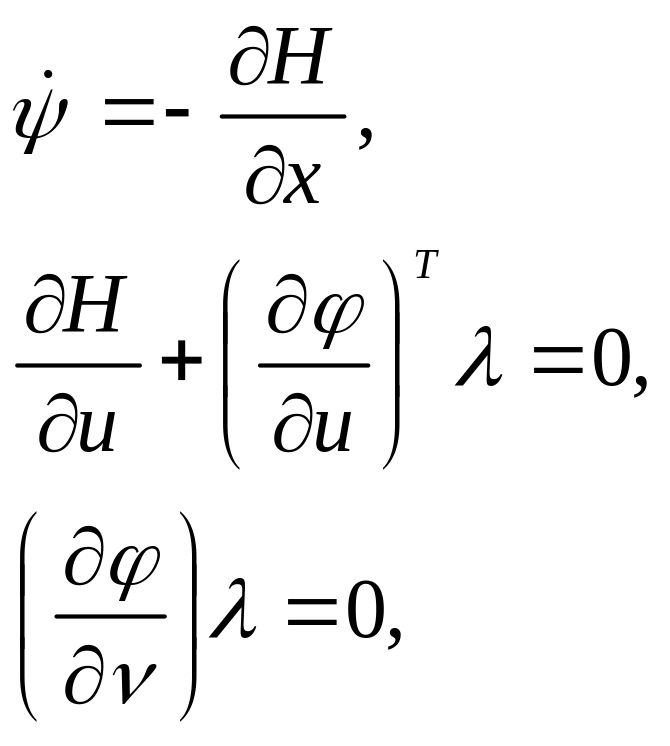 (6.30)
(6.30)
где
 с учетом уравнений динамики (6.25),
ограничений (6.28) и краевых условий.
с учетом уравнений динамики (6.25),
ограничений (6.28) и краевых условий.
В общем случае
управление u(t)
может представлять собой кусочно-непрерывную
вектор-функцию времени. Тогда в точке
разрыва управления необходимо использовать
условия Вейерштрасса-Эрдмана, которые
для данного случая принимают вид:
 .
.
Эти
условия означают непрерывность
 и
и
 на оптимальной траектории во всех её
угловых точках
на оптимальной траектории во всех её
угловых точках
 .
.
В частном случае
для линейной системы и квадратичного
критерия:

где
матрица Q
неотрицательно
определена, а R
положительно определена.
Уравнения
Эйлера-Лагранжа имеют вид:
 , (6.32)
, (6.32)
где
 ,
,
 .
.
Краевые
условия для этой задачи необходимо
выбрать в виде:

Последнее
из уравнений в (6.32) имеет решение:
 т.е.
т.е.
 т.е.
т.е.
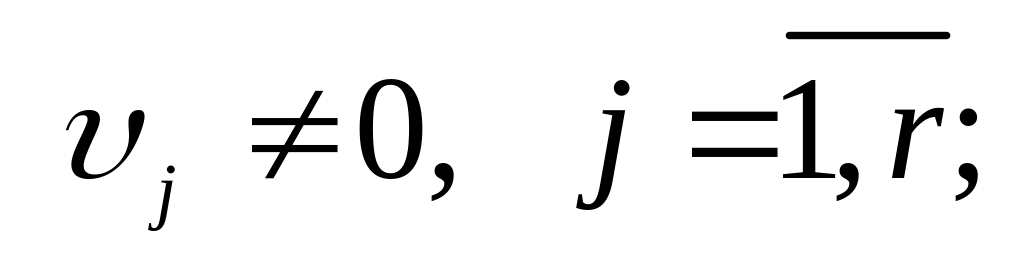
 т.е.
т.е.

 .
.
Если
а
 ,
то, очевидно, из (6.28) следует, что
,
то, очевидно, из (6.28) следует, что
 и система (6.32) принимает обычный вид:
и система (6.32) принимает обычный вид:

соответствующий
случаю, когда на управление не накладываются
ограничения.
Если
 = 0, то из (6.28) следует,
= 0, то из (6.28) следует,
 и управление достигает граничного
значения.
и управление достигает граничного
значения.
Пример. 6.4.
Определить оптимальное управление
скалярным объектом,

причем такое, что
 и которое минимизирует функционал
и которое минимизирует функционал
 ,
где q > 0, r > 0. Граничные условия
имеют вид:
,
где q > 0, r > 0. Граничные условия
имеют вид:

Решение.
После
ввода ограничения (6.28) функция Лагранжа
для задачи имеет вид:
 а
следовательно, управления (6.32) можно
записать совместно с уравнением динамики
объекта и преобразованным ограничением
а
следовательно, управления (6.32) можно
записать совместно с уравнением динамики
объекта и преобразованным ограничением
-

-

-

-


-

Третье уравнение
имеет решения:
-

-

-

Рассмотрим эти
случаи.
Случай
1.
Из пятого уравнения следует, что
 а
первые два и четвертое принимают вид:
а
первые два и четвертое принимают вид:
 . (6.33)
Решая
характеристическое уравнение системы
дифференциальных уравнений
. (6.33)
Решая
характеристическое уравнение системы
дифференциальных уравнений
 получим
значение характеристических чисел
получим
значение характеристических чисел
 Отметим, что
Отметим, что
 .
Общее решение имеет вид:
.
Общее решение имеет вид:
 Из
граничных условий находим, что С2
=
0 и, как следствие:
Из
граничных условий находим, что С2
=
0 и, как следствие:
 (6.34)
отсюда и из (6.33)
получаем:
(6.34)
отсюда и из (6.33)
получаем:
 (6.35)
Управление
(6.35) имеет место для тех значений x,
для которых справедливо неравенство
(6.35)
Управление
(6.35) имеет место для тех значений x,
для которых справедливо неравенство
 .
Случай
2 и 3. Если
только
= 0, то из пятого уравнения следует, что
.
Случай
2 и 3. Если
только
= 0, то из пятого уравнения следует, что
 ,
т.е.
,
т.е.
 принимает граничные значения.
Используя
полученные результаты, зависимость
управления от координат можем изобразить
на плоскости (x,u)
(рис. 6.4), а аналитически представить в
виде системы
уравнений:
принимает граничные значения.
Используя
полученные результаты, зависимость
управления от координат можем изобразить
на плоскости (x,u)
(рис. 6.4), а аналитически представить в
виде системы
уравнений:
 Рис. 6.4.
График зависимости u
= u(x)
Рис. 6.4.
График зависимости u
= u(x)
 (6.36)
Рассмотрим
поведение системы при a
< 0.
Положим, что начальная точка
(6.36)
Рассмотрим
поведение системы при a
< 0.
Положим, что начальная точка
 .
Тогда в начальный момент включаем, в
соответствии с (6.36), управление u
= -u0
и
уравнение динамики принимает вид:
.
Тогда в начальный момент включаем, в
соответствии с (6.36), управление u
= -u0
и
уравнение динамики принимает вид:
 для решения которого можем записать:
для решения которого можем записать:
 Очевидно,
что решение устойчиво и при некотором
t1,
значение координаты x(t)
достигает границы
Очевидно,
что решение устойчиво и при некотором
t1,
значение координаты x(t)
достигает границы
 ,
причём
,
причём
 ,
и
включается управление
,
и
включается управление
 .
При этом траектория описывается
уравнением
.
При этом траектория описывается
уравнением
 откуда
следует, что решение также устойчиво,
а из начального условия следует, что С1
=
.
В целом
траектории эволюции системы представлены
на рис. 6.5. При a
> 0
и начальной точке x(0)
>
решение имеет вид (рис. 6.6):
откуда
следует, что решение также устойчиво,
а из начального условия следует, что С1
=
.
В целом
траектории эволюции системы представлены
на рис. 6.5. При a
> 0
и начальной точке x(0)
>
решение имеет вид (рис. 6.6):

 Рис. 6.5.
Траектории системы при a
<
0 Рис. 6.6. Траектории системы при a
>
0
Рис. 6.5.
Траектории системы при a
<
0 Рис. 6.6. Траектории системы при a
>
0
Если
 ,
то система неустойчива, т.к. при
,
то система неустойчива, т.к. при
 Если
Если
 ,
то при росте t
величина
координаты
x(t)
уменьшается и достигает величины
,
когда включается управление
,
то при росте t
величина
координаты
x(t)
уменьшается и достигает величины
,
когда включается управление
 Момент переключения определяется
соотношением:
Момент переключения определяется
соотношением:
 .
Далее
эволюция системы описывается выражением
.
Далее
эволюция системы описывается выражением
 из
которого следует, что в этом случае
система устойчива.
Несколько
иная ситуация при решении возникает,
если, например, в задаче фиксированы t0
и tf,,
и при ограничениях вида (6.24) требуется
достичь максимального изменения по
одной из координат, или требуется перейти
из одной точки в фазовом пространстве
в другую за минимальное время. Рассмотрим
первую из этих задач.
Пример
6.5.
Для динамической системы
из
которого следует, что в этом случае
система устойчива.
Несколько
иная ситуация при решении возникает,
если, например, в задаче фиксированы t0
и tf,,
и при ограничениях вида (6.24) требуется
достичь максимального изменения по
одной из координат, или требуется перейти
из одной точки в фазовом пространстве
в другую за минимальное время. Рассмотрим
первую из этих задач.
Пример
6.5.
Для динамической системы
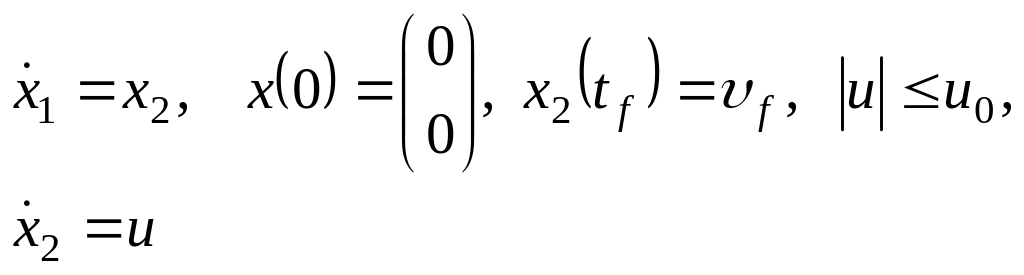 (6.37)
найти
управление, обеспечивающее максимальное
удаление от начальной точки по координате
x,
т.е.
(6.37)
найти
управление, обеспечивающее максимальное
удаление от начальной точки по координате
x,
т.е.
 (6.38)
Решение.
Используя структуру лагранжиана с
учетом ограничения (6.28):
(6.38)
Решение.
Используя структуру лагранжиана с
учетом ограничения (6.28):
 и
уравнения Эйлера-Лагранжа, можем
записать:
и
уравнения Эйлера-Лагранжа, можем
записать:
 Последнее
равенство возможно только при
=
0, т.к., если
Последнее
равенство возможно только при
=
0, т.к., если
 ,
то из предыдущего равенства следует,
что конечное управление, удовлетворяющее
ограничению, не существует. Если же
=0,
то из ограничения следует, что управление
u(t)
принимает предельные значения +u0
или –u0.
Если только
,
то из предыдущего равенства следует,
что конечное управление, удовлетворяющее
ограничению, не существует. Если же
=0,
то из ограничения следует, что управление
u(t)
принимает предельные значения +u0
или –u0.
Если только то ни одно из управлений
то ни одно из управлений
 не решает поставленной задачи.
Тогда
полагаем, что существует разрывное
решение для u(t)
такое, что
не решает поставленной задачи.
Тогда
полагаем, что существует разрывное
решение для u(t)
такое, что
 (6.39)
где
(6.39)
где
 -
момент переключения, который нужно
определить.
Используя
управление в виде (6.39), уравнения динамики
и краевые условия (6.37), получим после
интегрирования:
-
момент переключения, который нужно
определить.
Используя
управление в виде (6.39), уравнения динамики
и краевые условия (6.37), получим после
интегрирования:
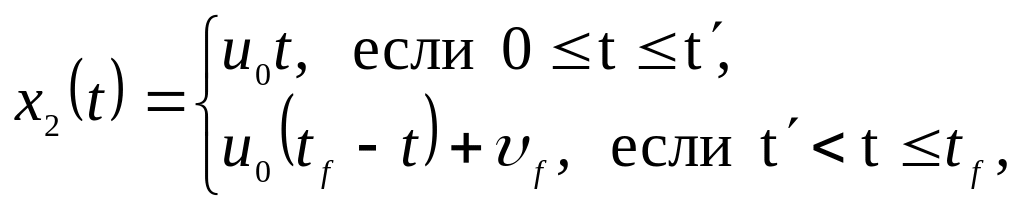 откуда
в силу требований непрерывности x2(t)
следует, что
откуда
в силу требований непрерывности x2(t)
следует, что
 Для
координаты x1(t)
после интегрирования первого
дифференциального уравнения динамики
системы, с учётом начального условия
Для
координаты x1(t)
после интегрирования первого
дифференциального уравнения динамики
системы, с учётом начального условия
 ,
получим:
,
получим:
 (6.40)
Из
требований непрерывности x1(t)
можно записать
(6.40)
Из
требований непрерывности x1(t)
можно записать
 и в
итоге, подставив значения С1
и
и в
итоге, подставив значения С1
и
 в
(6.40), получим значение x1max.
Решение
последних примеров показывает, что
решение двухточечных краевых задач
достаточно нестандартно в каждом из
даже таких простых случаев, рассмотренных
нами, а более сложные задачи подобного
типа приводят к сложным алгебраическим
нелинейным системам уравнений. Поэтому
целесообразно разработать единую
методику решения задач управления с
ограничениями вида неравенств.
в
(6.40), получим значение x1max.
Решение
последних примеров показывает, что
решение двухточечных краевых задач
достаточно нестандартно в каждом из
даже таких простых случаев, рассмотренных
нами, а более сложные задачи подобного
типа приводят к сложным алгебраическим
нелинейным системам уравнений. Поэтому
целесообразно разработать единую
методику решения задач управления с
ограничениями вида неравенств.

![]() . (6.24)
. (6.24)![]()
![]() .
.![]() , (6.25)
, (6.25)![]() из начальной точки
из начальной точки
![]() в конечную
в конечную
![]() ,
минимизируя функционал
,
минимизируя функционал ,
(6.26)
,
(6.26)![]() наложены
ограничения:
наложены
ограничения:![]() (6.27)
(6.27)![]() такого, что
такого, что![]() . (6.28)
. (6.28)![]()
![]() . (6.29)
. (6.29)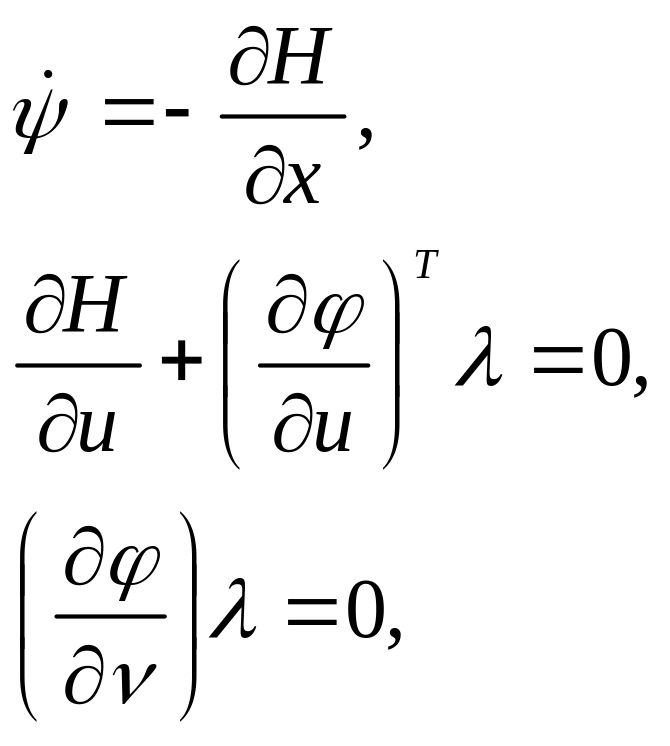 (6.30)
(6.30)![]() с учетом уравнений динамики (6.25),
ограничений (6.28) и краевых условий.
с учетом уравнений динамики (6.25),
ограничений (6.28) и краевых условий.![]() .
.![]() и
и
![]() на оптимальной траектории во всех её
угловых точках
на оптимальной траектории во всех её
угловых точках
![]() .
.
![]() , (6.32)
, (6.32) ,
,
 .
.![]()
 т.е.
т.е.
 т.е.
т.е.
 т.е.
т.е.

 .
.![]() ,
то, очевидно, из (6.28) следует, что
,
то, очевидно, из (6.28) следует, что
![]() и система (6.32) принимает обычный вид:
и система (6.32) принимает обычный вид:![]()
![]() = 0, то из (6.28) следует,
= 0, то из (6.28) следует,
![]() и управление достигает граничного
значения.
и управление достигает граничного
значения.![]()
![]() и которое минимизирует функционал
и которое минимизирует функционал
![]() ,
где q > 0, r > 0. Граничные условия
имеют вид:
,
где q > 0, r > 0. Граничные условия
имеют вид:
![]()
 получим
значение характеристических чисел
получим
значение характеристических чисел
 Из
граничных условий находим, что С2
=
0 и, как следствие:
Из
граничных условий находим, что С2
=
0 и, как следствие:
 Рис. 6.4.
График зависимости u
= u(x)
Рис. 6.4.
График зависимости u
= u(x)
 Рис. 6.5.
Траектории системы при a
<
0 Рис. 6.6. Траектории системы при a
>
0
Рис. 6.5.
Траектории системы при a
<
0 Рис. 6.6. Траектории системы при a
>
0
 и в
итоге, подставив значения С1
и
и в
итоге, подставив значения С1
и
