Системы с переменной областью управления

Пусть движение объекта описывается уравнением

(6.63)

причем вектор должен удовлетворять соотношениям

(6.64)

При фиксированном значении соотношения (6.64) определяют область допустимых значений управления . Эта область изменяется вместе с изменением вектора состояний и является переменной.

Управление будем называть допустимыми, если оно кусочно-непрерывно и принимает значения из .

Найдем решение для задачи о переводе системы (6.63) из начальной точки в конечную с помощью допустимых управлений ( и не фиксированы), которые минимизируют функционал

(6.65)

Введем понятие регулярности для траекторий. Точку , где Х допустимая область решений, назовем регулярной, если для любого векторы

линейно независимы. Множество - это множество так называемых активных индексов таких, что в точке (x,u)

Тогда справедливо утверждение, что, если - допустимое управление, переводящее систему из в , и если соответствующая управлению траектория регулярна, то для оптимальности управления и траектории необходимо существование ненулевого непрерывного вектора , кусочно-непрерывных функций и , таких что:

1. вектор-функция удовлетворяет системе уравнений

(6.66)

где ;

2. функция постоянна и удовлетворяет условию

(6.67)

3. выполняется условие максимума, т.е. для

(6.68)

4. имеют место соотношения

(6.69)

5. для (кроме конечного числа значений) справедливы равенства

(6.70)

Пример 6.11. Найти оптимальное управление, минимизирующее функционал

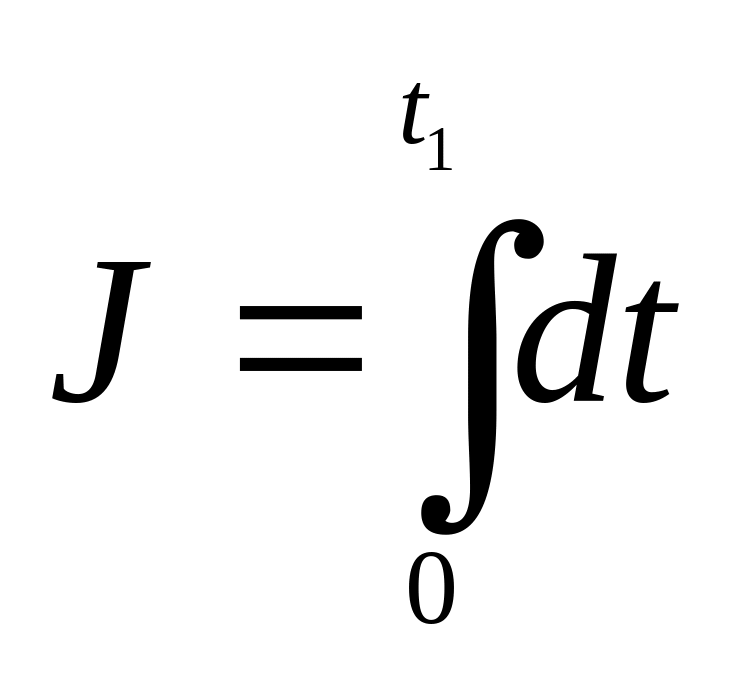
для системы

при условиях

.

Решение. В соответствии с условием составляем гамильтониан

и функцию ограничения

с учётом аналитического вида функции ограничения, наложений на управление (см. рис. 6.9).

Рис. 6.9. Определение допустимой области значений управления

Составим все уравнения (6.60) – (6.70) для нашей задачи:

(1)

, (2)

, (3)

, (4)

. (5)

Очевидно, что для перемещения системы из в начало координат необходимо управление, приближающее к конечной точке. Тогда из (4), (5), а затем (3) следует, что ему , то и значение гамильтониана (3) не зависит от . Если же положить , то:

(6)

или

. (7)

Однако управления (7) не обеспечивает движение , поэтому на этом этапе

. (8)

Подставляя это управление в уравнение динамики и решая его с учётом начального условия, получим

; . (9)

Учтём, что в момент мы должны произвести переключение управления на . Определим момент переключения:

. (10)

Для продолжаем управление с использованием

,

подставляя его в уравнение динамики с учётом граничного условия , .

, , .

Отсюда следует, что

, (11)

а следовательно, в момент

будет достигнуто начало координат. Таким образом, искомое управление имеет вид (см. рис. 6.10):

а соответствующая траектория

Рис. 6.10. Графики оптимального управления и соответствующей траектории

Перейдём теперь к более прикладным задачам и рассмотрим, например, динамическую, однопродуктовую модель экономики (объем трудовых ресурсов постоянен)

, (6.71)

где k(t) – удельный объем основных фондов, - норма амортизации, p(k) – удельный объем выпуска продукции, выражаемый производственной функцией, u(t) – объем удельного потребления.

Управляемым параметром модели является объем потребления, на который наложим вполне естественное ограничение

(6.72)

т.е. потребление должно быть не меньше некоторой минимальной величины («прожиточного минимума») и не превышать объема произведенной продукции, выраженной в денежных единицах. Начальное состояние в производственной сфере задано .

Требуется найти такую функцию , которая бы обеспечила максимум потребления на всем интервале функционирования системы, т.е.

, (6.73)

где - коэффициент дисконтирования, учитывающий обесценивание отложенного потребления, - не ограничено.

Очевидно, что неравенство (6.72) задает переменную область допустимых управлений на плоскости (k,u). Учитывая, что для производственной функции характерны свойства , и при , допустимая область имеет характер, изображенный на рис. 6.11.

k

Рис. 6.11. Допустимая область управлений

Функция Н для данной задачи имеет вид

. (6.74)

Ограничения (6.64), которые имеют вид (6.72), запишем следующим образом

(6.75)

Тогда необходимо решить задачу (6.66)-(6.70), имеющую в нашем случае структуру:

(6.76)

, (6.77)

, (6.78)

. (6.79)

Если то решения задачи не существует, так как система не может обеспечить даже минимальный уровень потребления.

Пусть тогда для (6.77) рассмотрим возможные варианты:

Из выражения (6.77) можем рассмотреть три случая:

1) (6.80)

2) (6.81)

3) (6.82)

Случай 1. Уравнения (6.71),(6.76) и (6.78) принимают вид:

(6.83)

(6.84)

. (6.85)

Если является левым корнем уравнения то (см. рис. 6.10) для основные фонды монотонно убывают, и решения задачи для длительного функционирования системы не существует.

Если , то k(t) растет, и, следовательно, убывает по модулю. В некоторый момент выполняется равенство и обращается в нуль (см. (6.85)), а мы вынуждены перейти к случаю 3.

Выбираем управление таким образом, чтобы фонды были стационарны, т.е.

(6.86)

где соответствуют условию .

Случай 2. Уравнения (6.71), (6.76) и (6.78) принимают вид:

(6.87)

(6.88)

. (6.89)

Для такое уравнение использовать нельзя, т.к. уравнение (6.86) показывает, что в этом случае k(t) будет неограниченно убывать, и стационарного процесса мы не добьёмся. Но если , то, используя (6.86), для уравнения (6.85) получим

(6.90)

Из уравнения (6.84) следует, что монотонно убывает, а следовательно, и в момент т.е. в точке достигает значения и обращается в нуль и мы переходим к случаю 3.

где определено равенством (6.86).

Таким образом, оптимальное управление для рассмотренной задачи, приводящее к стационарным состояниям, имеет вид, представленный на рис. 6.13.