1. Классического типа, когда ограничения задаются в виде равенств:

.

2. Неклассического типа, когда ограничения задаются в виде включений, которые приводят к ограничениям в виде неравенств:

.

Задачи неклассического типа можно преобразовать к классическому типу с помощью дополнительных переменных, что, однако, усложнит характер решаемой краевой задачи.

По типу краевых условий можно различать:

1. Задачи с фиксированными (закрепленными) концами, когда допустимые множества X₀ и X_f в (6.5) состоят из одной точки:

2. Задачи с подвижными концами, когда X₀ или X_f, либо X₀ и X_f одновременно в (6.5) состоят из множества точек, т.е. подвижными являются левый или правый конец или оба конца подвижны одновременно.

Предельным случаем "подвижности" является случай, когда правый конец x_f является просто свободным, без каких-либо наложенных условий. В этом случае допустимое множество X_f совпадает со всем фазовым пространством Rⁿ.

Можно выделять и задачи с фиксированными и нефиксированными моментами начала и конца процесса управления.

По структуре критериев оптимальности можно различить:

1. Задачу Больца, в которой критерий имеет вид:

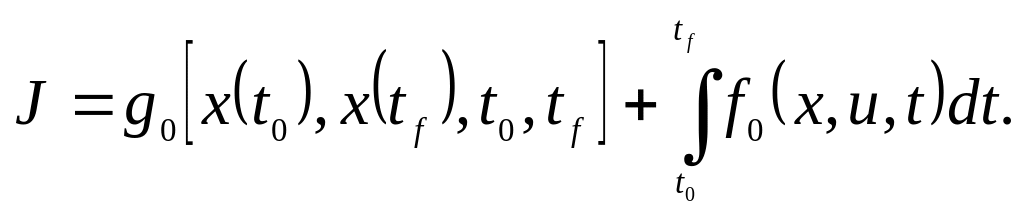
2. Задачу Лагранжа, где

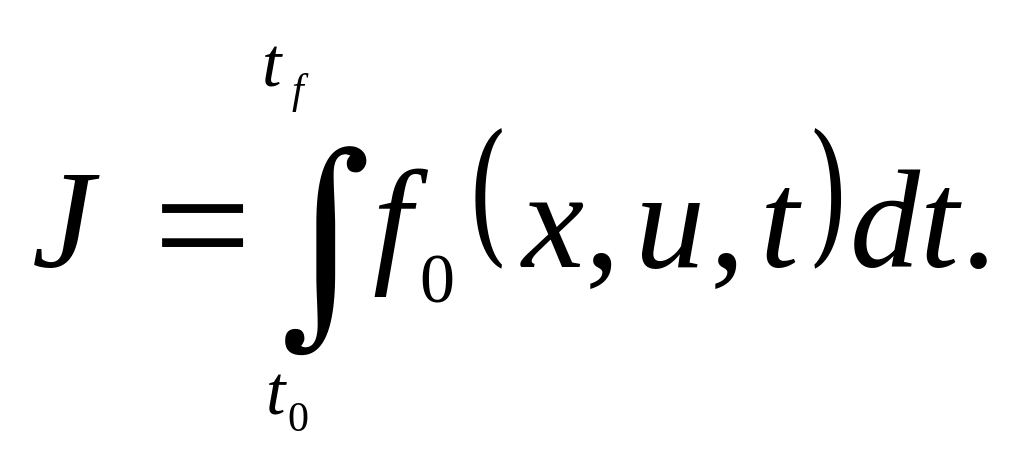
3. Задачу Майера, в которой критерий приобретает точечный характер

.

Задачу Майера в частном случае, когда функционал имеет вид , называют задачей терминального управления, а если J=t_f–t₀, то такую задачу называют задачей максимального быстродействия.

Как известно, путем преобразования переменных можно перейти от одной задачи к другой, и в этом смысле они эквивалентны [2]. Однако в реальных задачах для наглядности лучше решать задачи оптимизации в исходном виде без преобразования переменных. При использовании численных методов решения краевых оптимизационных задач целесообразно приведение условий задачи к некоторому стандартному виду с обратным преобразованием полученных результатов, выполняемых на ЭВМ.

6.2. Задача управления системой при фиксированных концах и времени процесса

Эта задача формулируется как задача Лагранжа: требуется найти допустимую пару (x(t),u(t)), удовлетворяющую: уравнениям динамики (эволюции) системы

, (6.10)

ограничениям в виде равенств (уравнений), налагаемым на координаты и управление

, (6.11)

краевым условиям

, (6.12)

и обеспечивающую минимум функционалу

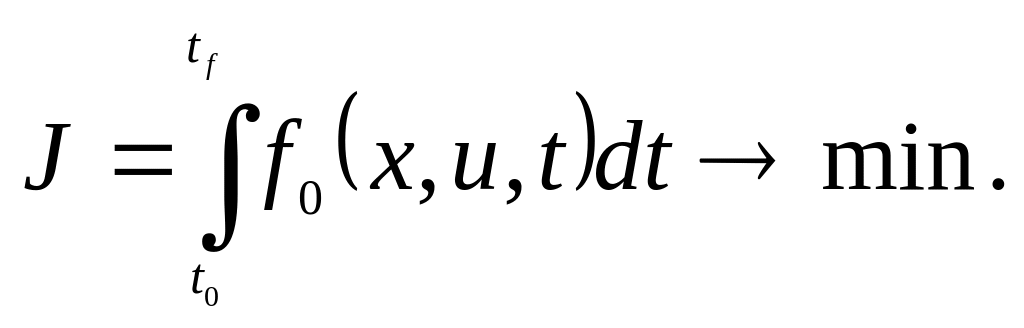(6.13)

Используя методы вариационного исчисления (см. приложение 1), можно записать функцию Лагранжа

(6.14)

и необходимое условие экстремума функционала, выражаемое уравнениями Эйлера-Лагранжа (П1.15), где варьируемыми переменными являются координаты векторов x(t) = ( x₁(t),…, x_n(t))^Т и u(t) = (u₁(t),…, u_r(t))^T­:

(6.15)

Если ввести функцию Гамильтона (П1.28)

(6.16)

то система уравнений (6.15) приобретает вид:

(6.17)

где последнее уравнение часто называют условием стационарности.

Оптимальную пару (x^*(t),u^*(t)) находим из решения системы дифференциальных уравнений (6.15) или (6.17) совместно с (6.10) с использованием краевых условий (6.12). Параметры и , возникающие при решении задачи, участвуют в решении задачи, но не требуют своего обязательного окончательного определения. Величину полагают равной –1, т.к. обычно решают задачу минимизации (см. Приложение 1).

Пример. 6.1. Требуется объект, описываемый системой уравнений , перевести из начального состояния x₁(t₀) = x₂(t₀) = 1 в начало координат за время Т =1 (т.е. t₀=0, t_f = 1, x₁(t_f) = x₂(t_f) = 0), обеспечив минимум функционала

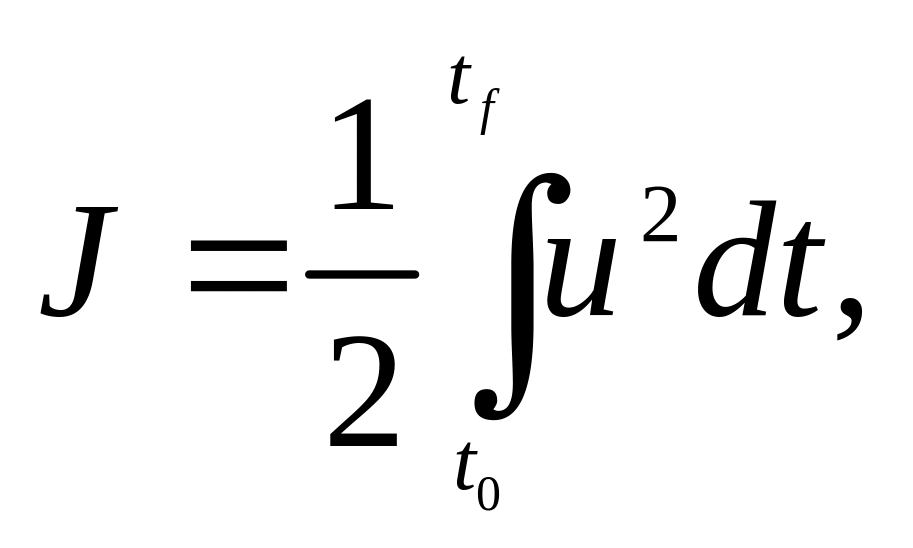
который отражает "энергетические" затраты на управление.

Решение. Составляем функцию Гамильтона:

и соответствующие уравнения Эйлера-Лагранжа:

Решая последовательно эти уравнения, получим управление , подставляя которое в уравнения для , а затем для , получим выражения:

константы в которых найдем из краевых условий и получим С₃ = С₄ = 1, С₁ = -18, С₂ = -10, а в итоге оптимальное управление и траектория имеют вид:

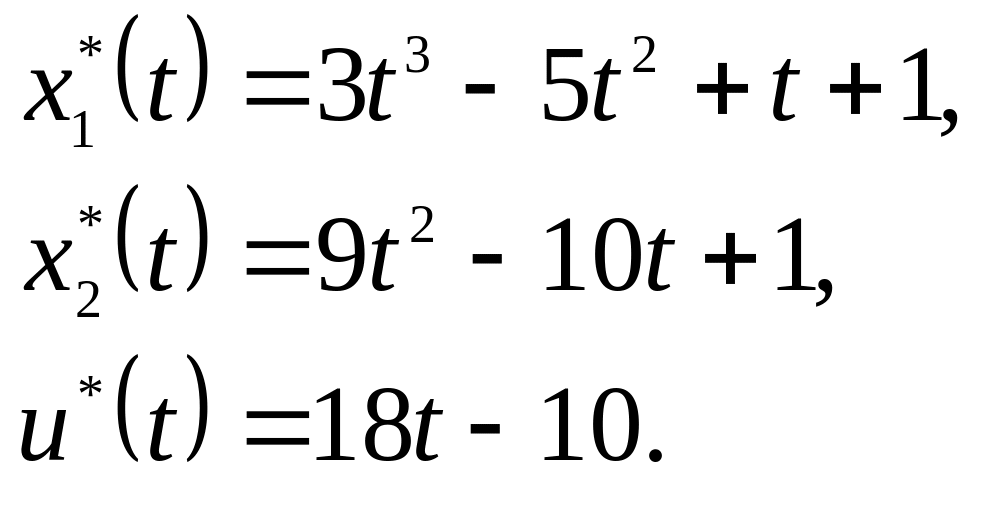
6.3. Задача с подвижными концами и нефиксированным временем процесса управления

В этом случае задача оптимального управления может быть задачей Лагранжа, Больца или Майера. Формулируется она следующим образом: найти допустимую пару (x(t),u(t)) такую, что:

, (6.10)

, (6.11)

удовлетворяющую краевым условиям

(6.18)

где t_0, t_f и не фиксированы, и доставляющую функционалу

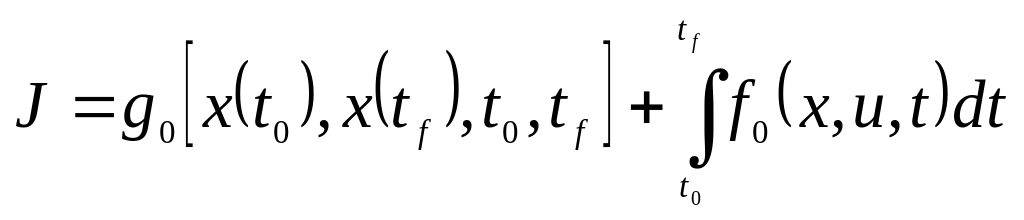(6.19)

минимальное значение.

Используя метод Лагранжа, преобразуем эту задачу в простейшую задачу Больца:

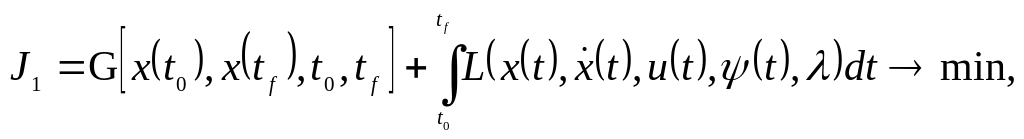(6.20)

где

(6.21)

Как следует из Приложения 1, уравнения Эйлера-Лагранжа соответствуют системе (6.15) или (6.16), условия трансверсальности, соответствующие подвижности границ, принимают вид:

(6.22)

а условия трансверсальности, соответствующие подвижности концов t₀ и t_f , принимают вид:

(6.23)

Отыскание оптимальной пары (x^*(t),u^*(t)) и начального и конечного моментов процесса управления t₀ и t_f производится совместным решением (6.17) с учетом (6.10), (6.11), (6.18), (6.22) и (6.23).

Пример. 6.2. Рассмотрим объект, описываемый в задаче предыдущего раздела с теми же начальными условиями и критерием оптимальности, но на правом конце полагаем, что t_f и x₂(t_f) свободно, и должно выполняться условие x₁(t_f) = - .

Решение. Очевидно, что функции Лагранжа и Гамильтона не изменяются, а следовательно, и уравнения Эйлера-Лагранжа и их общие решения тоже. Часть констант, а именно С₃ и С₄ легко находятся из условий при t = 0: С₃ = С₄ = 1.

Далее составляем функцию , и из условий трансверсальности на правом конце из (6.22), (6.23) и граничного условия получим систему уравнений:

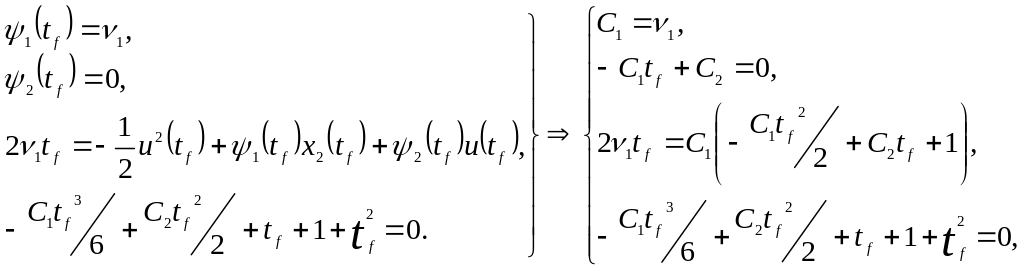
из которой находим С₁, С₂ и t_f , а следовательно, находим оптимальную пару (x^*(t),u^*(t)) и время окончания процесса управления:

Пример. 6.3. Требуется перевести объект из предыдущей задачи из начала координат в точку с координатами x₁ = S, x₂ = 0 за минимальное время при наличии ограничения на энергетические затраты

Решение. В связи с постановкой задачи критерий можно представить в одном из видов:

Ограничение в виде интеграла (так называемое изопериметрическое условие) можно заметить, используя введение новой переменной и краевых условий для неё:

,

Тогда задача принимает вид:

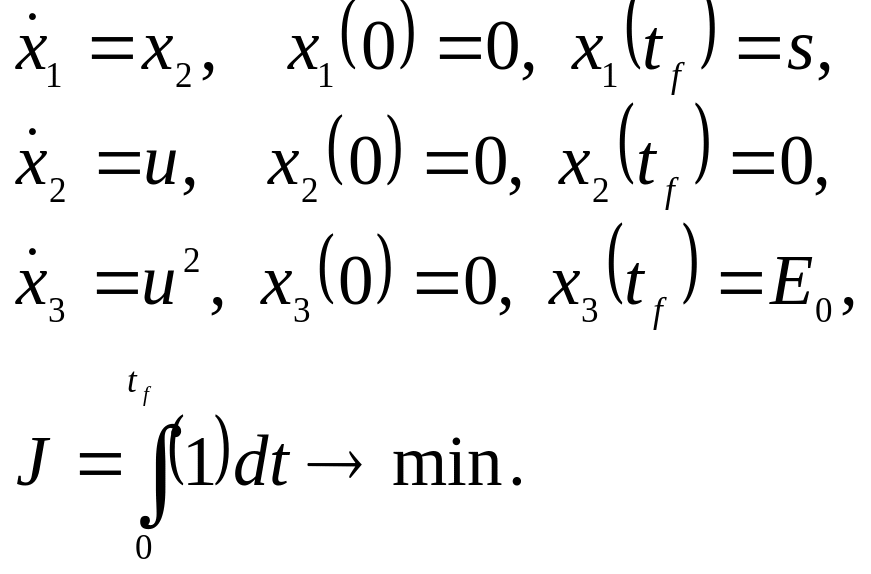
В этой задаче требуется определить оптимальную пару (x^*(t),u^*(t))и время окончания процесса t_f .

Составим функцию Гамильтона, вспомогательную функцию G:

и соответствующие уравнения Эйлера-Лагранжа (6.17):

С учетом краевых условий и условия трансверсальности (6.23), которое принимает вид:

можем найти (после интегрирования уравнений движения):

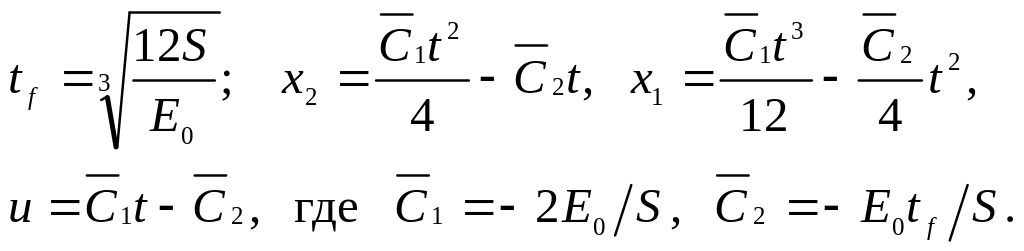
Таким образом, оптимальное управление u^*(t)принимает вид:

Отметим, что условие трансверсальности не использовалось, хотя оно может потребоваться для нахождения множителей Лагранжа, которые нам в данном случае не нужны для решения.