9. Выборка из нормального распределения. Представление Хи-квадрат распределения с помощью нормальных. Распределение Стьюдента. Распределение Фишера-Снедекора. Лемма Фишера.
Пусть
выборка из N(0,
1).
Введем некоторые распределения , используемые в матстатистике.
Рассмотрим случайную
величину
.
Говорят что
имеет
-распределение(или
распределение Пирсона ) с n
степенями
свободы. Плотность распределения
величины
имеет вид
где
- гамма – функция Эйлера, определяемая
равенством
Семейство
-распределение
является подмножеством двухпараметрического
семейства гамма-распределений Г(b,p),
p,b
0,
с плотностями
При b=1/2, p=n/2, n N. Известное свойство , что сумма двух независимых гамма-распределений Г(b,p) и Г(b,q) снова имеет гамма-распределение Г(b,p+q) , здесь следует непосредственно из представления в виде суммы квадратов незвис нормальных величин.
Пусть сл. в. Y
независима от
.
Рассмотрим случайную вел-ну
Распределение
величины Tn
называется
распределением Стьюдента с n
степенями свободы. Соответствующая
плотность распределения имеет вид
Отметим , что плотность распределения Стьюдента симметрична относительно нуля.
Распределения
Фишера-Снедекора
F(n1,n2)
определяется как распределение сл. в.
независимы
и распределены как
и
. Плотность распределения Фишера-
Снедекора представляется в виде
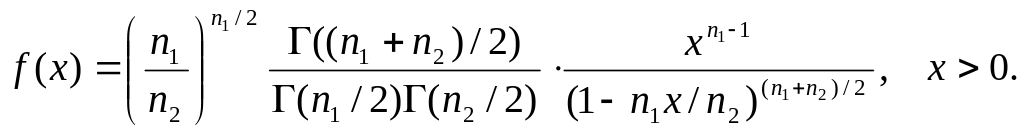
Лемма Фишера.
Пусть X1,X2,…Xn - выборка из нормального распределения N(a, σ2). Тогда
1)
;
2) и S2– независимы
3)
имеет
-распределение
с (n-1)
степенью свободы;
4)
имеет
распределение Стьюдента с (n-1)степенью
свободы.
10.Постановка задачи доверительного оценивания. Общий метод построения доверительных интервалов. Примеры построения доверительных интервалов для параметров нормального закона (случай одной и двух выборок) (Л-П)
До сих пор мы говорили о точечном оценивании параметров. Будем строить множество: пусть - статистический эксперимент. Доверительной оценкой параметра уровня значимости (или 1ровня доверия ) называется статистика Ĥ: , где С –некоторая совокупность подмножества Ĥ,
; мн-во, построенное по результатам наблюдений, кот. с вероятностью накрывает истинное значение параметра
Замечание: необходимо накладывать какое-либо ограничение на множество С. Пусть (одномерный параметр), С – совокупность интервалов
. В этом случае доверительная оценка - доверительный интервал.
Альтернативное определение: Доверительный интервал уровня значимости наз-ся пара статистик T1, T2 : ; .
Основные методы
построения ДИ.
Пусть удается найти функцию
а) Распределение
не зависит от параметра
б)
,тогда
-
интервал
в) Распределение
- известно, т.е. можно найти
Примеры построения доверительных интервалов для параметров нормального закона :
Пример: Нормальное
распределение. Пусть х1…хn
– выборка из N(a,
)
распределения. Построить ДИ для а, если
-
неизв. Выберем
,
не зависящую от второго параметра.
Решение:
.
По лемме Фишера имеет распределение
Стьюдента:
.
Выберем
:
(используя таблицу,
Находим
.
Т.о.
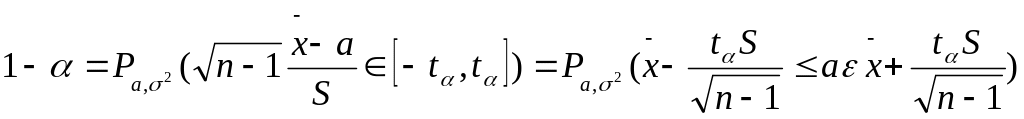
S-выб.дисперсия.
ДИ
2. Строим ДИ для
(а – неизв); по п.3 лемме Фишера:
.
Очевидно, что
,
может быть выбраны неоднозначно. Решение
Х2
{рисунок}
Длина ДИ характеризует
точность оценки. В случае Стьюдента
построенный доверительный интервал
кратчайший. Для
- более сложная задача, поэтому находят
ДИ из условий
;
.
Решение задачи
.
{Если нет априорной информации, нужно
брать 2-сторонний интервал, если есть –
односторонний}
Пусть
- независимые.
- неизвестна (мешающий параметр). Построим
ДИ для a-b.
Согласно лемме Фишера:
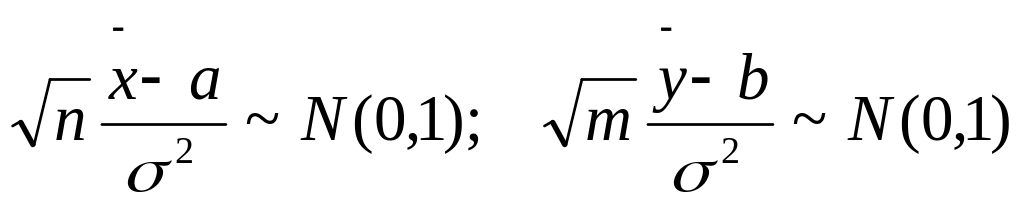Т.о.
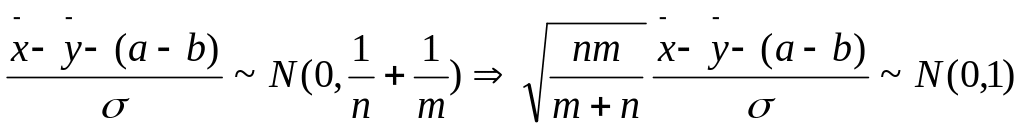
По лемме Фишера
п.3
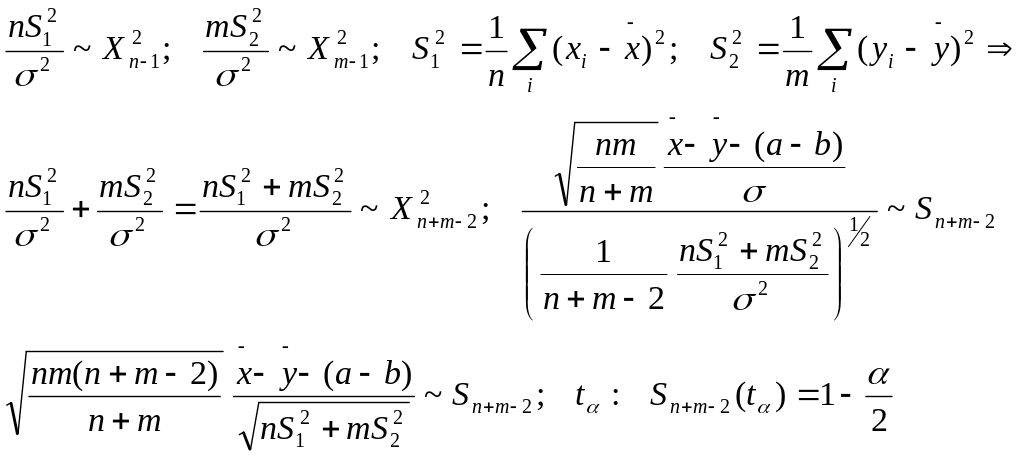
ДИ:
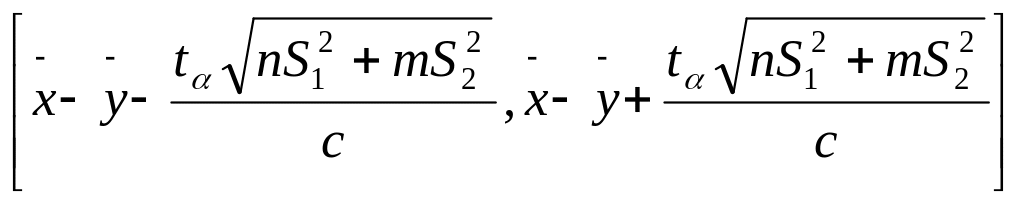для параметра (a-b)
{считается что
задано}
Построим ДИ.
4.
ДИ для
П.3 леммы Фишера :
;
По замечанию к лемме Фишера получим
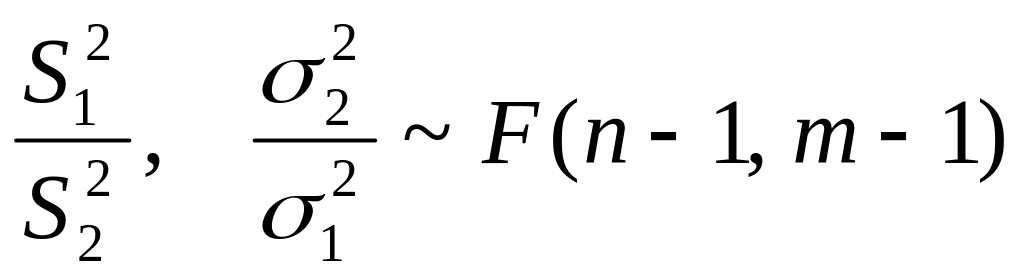- распределение Снедекора
- ДИ для
Примечание к
примеру 3: мешающий параметр
- одномерный, если
,
т.е. могут быть разные, т.е. мешающий –
двумерный, то задача не решена, проблема
Беренса-Фишера
{рисунок}
Доверительная оценка Ĥ называется состоятельной, если она стягивается в точку.
Если Ĥ-
ДИ, то состоятельность равносильна
тому, что
.
В примерах 1-4 ДИ – состоятельные (т.к. в нормальных законах)
Пример5:
Пусть x1…xn
– выборка из
;
- функция распределения х1.
Пусть
при фиксиров. х – монотонная функция
от
.
Тогда в качестве
.
Отметим
;
,
где
- функция распределения
11.Асимптотические доверительные интервалы. Построение асимптотических доверительных интервалов на базе асимптотически нормальной оценки параметра. Построение доверительных интервалов на базе ОМП в регулярном случае. Пример (Распределение Бернулли).
Определение: Послед-ть областей
-
ас.д.область уровня α для θ,
если
Если
-
ас.д.и.
Замечание:
если
- ас.д.и.ур.α
Способ построения:
Найти
,
т.ч.
а)
б)
Построение ас.д.и. на базе ас.норм.оценки
Пусть δ –
ас.норм.оценки, т.е.
т.е.
Пусть
Если удастся
выразить θ из
то находим д.и. в противном случае
Пусть δк(θ) – состоят. оценка для δ(θ)
(δ(θ)0) тогда
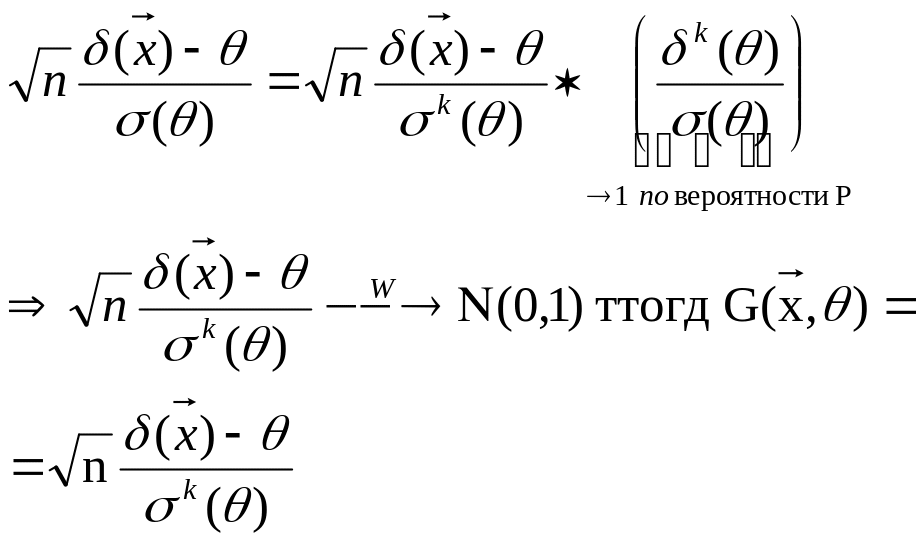
Пример: (распр. Бернулли)
x1…x2 – выборка из Bi (1,θ)
-------------------------------------------------------------------------
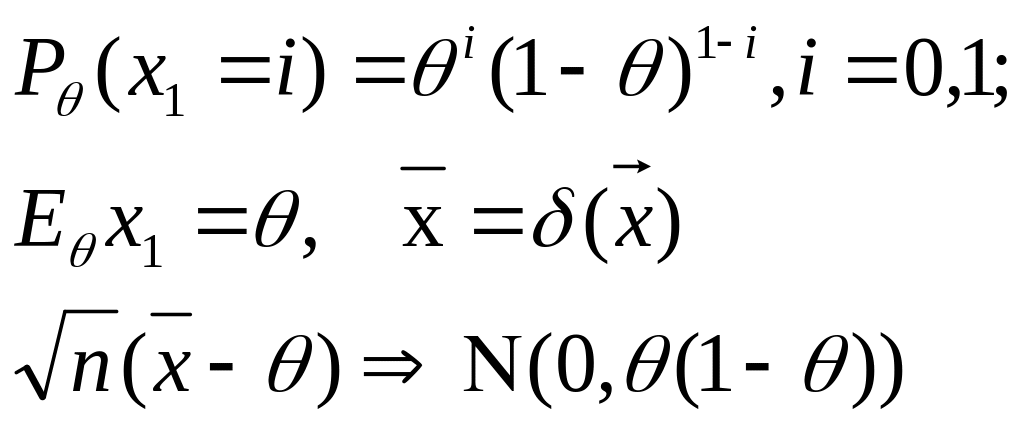
Интегральная теорема Муавра-Лапласа(ИТМЛ):
-------------------------------------------------------------------------
Итак
Находим х2. Решаем:
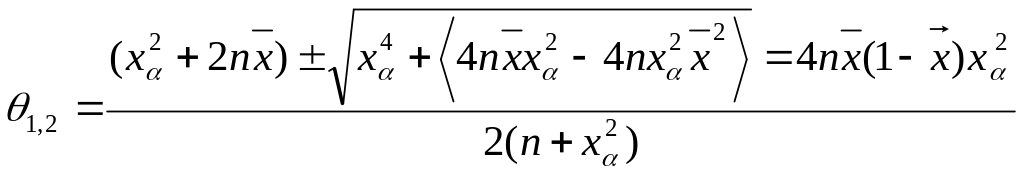
АДИ (асимпт, доверит, интервал)
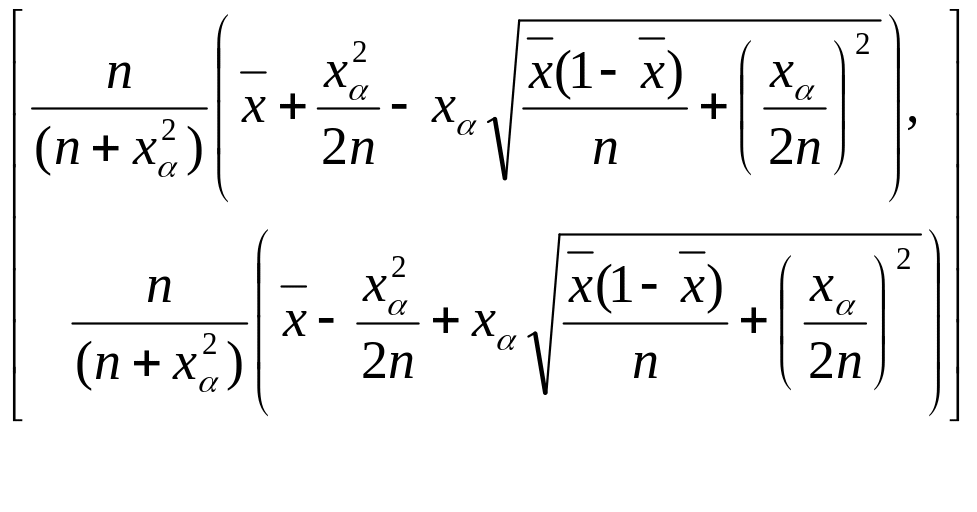
б) Вернемся
-
сост. оценка для
Пусть
Решаем
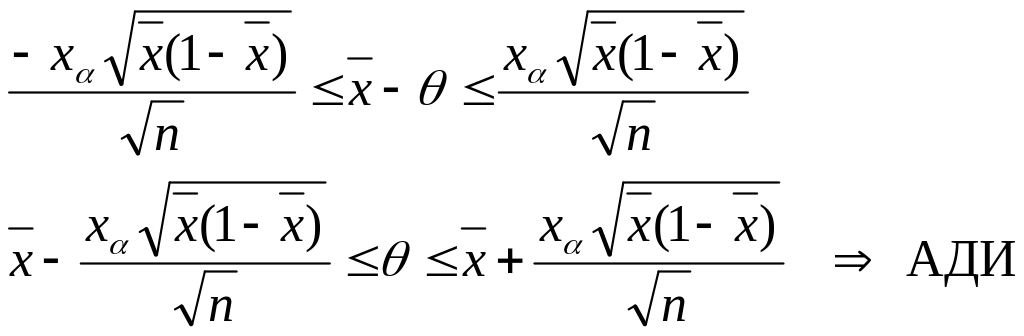
в)
тогда АДИ
