
- •Л1 02.09.09 Алгебра многочленов
- •§1: Многочлены как функции действительной переменной
- •§2 Алгебраическое определение кольца многочленов
- •§3 Кольцо многочленов над областью целостности
- •§4 Деление с остатком многочлена на двучлен (X- )
- •§5 Наибольшее возможное число корней в области целостности.
- •§6 Деление с остатком
- •§ 7 Наибольший общий делитель многочленов. Алгоритм Евклида.
- •§ 8 Наименьшее общее кратное двух многочленов.
- •§9 Многочлены не приводимые над полем
- •§10 Разложение многочлена в произведении нормированных не приводимых множителей
- •§11 Формальная производная многочлена
- •§12 Не приводимые кратные множители многочлена.
- •§ 13 Кратные корни многочлена
- •§14 Разложение многочлена по степеням двучлена
- •§15 Кольцо многочленов от n переменных
- •§16 Степень многочлена. Лексикографическое упорядочение членов многочлена.
- •§17 Разложение многочлена от n переменных в произведение не приводимых множителей
- •§18 Cсимметрические многочлены
- •§ 19 Основная теорема о симметрических многочленах.
- •§20 (Дополнение к теме нод). Результант 2 многочленов
- •§21 Многочлены над полем комплексных чисел
- •§ 22 Зависимость между корнями. Теорема Виета.
- •§23 Свойства мнимых корней многочлена с действительными коэффициентами
- •§24 Разложение многочлена над полем действительных чисел в произведение не приводимых множителей
- •§25 Решение кубических уравнений
- •§27 Решение уравнений 4 степени(Феррари)
- •§28 Теорема Штурма(отделение действительных корней многочлена)
- •§29 Отыскание рациональных корней многочлена
- •30 Т(Критерий не приводимости Эйзенштейна):
- •31 Простое алгебраическое расширение как линейное пространство.
- •32 Избавление от иррациональности
§28 Теорема Штурма(отделение действительных корней многочлена)
Пусть дан многочлен n степени с действительными коэффициентами (1)
По основной теореме алгебры многочлен имеет ровно n корней если многочлен имеет комплексные корни то они встречаются парами как комплексные сопряжённые. Комплексных корней всегда четное число, по этому число действительных корней с учетом кратности либо равно степени многочлена либо на четное число меньше, в частности любой многочлен не четной степени имеет худобы 1 действительный корень.
Представляет интерес определения
точного числа действительных корней
многочлена а также промежутков их
принадлежности. Можно показать, что все
действительные корни многочлена
принадлежат интервалу ![]()
![]()
Ответить на вопрос сколько многочлен имеет действительных корней в заданном интервале позволяет теорема штурма, в которой используются функции штурма.
Для построения ряда штурма выполняют следующую процедуру: находят производную многочлена как функции f(x) это будет некоторый многочлен с действительными коэффициентами. Для многочленов f(x) и f`(x) выполняют алгоритм похожий на алгоритм Евклида:
![]()
![]()
![]()
![]()
![]()
Если данный многочлен не имеет кратных
корней то в этом случае ![]() то последний остаток является многочленом
нулевой степени то есть числом.
Последовательность многочленов:
то последний остаток является многочленом
нулевой степени то есть числом.
Последовательность многочленов:![]() называется ряд функций штурма. В
дальнейшем нас будут интерисовать знаки
тех значений которые принимают функции
ряда штурма по этому функции образующее
последовательность (2) можно находить
с точностью до постоянного положительного
множителя.
называется ряд функций штурма. В
дальнейшем нас будут интерисовать знаки
тех значений которые принимают функции
ряда штурма по этому функции образующее
последовательность (2) можно находить
с точностью до постоянного положительного
множителя.
Т(Штурма): Если a,b
![]() и не являются корнями многочлена
f(x)не
имеющего кратных корней то число
действительных корней этого многочлена
принадлежащих интервалу (a,b),
и не являются корнями многочлена
f(x)не
имеющего кратных корней то число
действительных корней этого многочлена
принадлежащих интервалу (a,b),
![]() где s(x)
количество перемен знаков в ряде
функций штурма соответственно в точках
a,b.
где s(x)
количество перемен знаков в ряде
функций штурма соответственно в точках
a,b.
§29 Отыскание рациональных корней многочлена
Т1: Если рациональное число ![]() является корнем многочлена f(x)
то свободный член делится на p
а старший коэффициент делится на q.
является корнем многочлена f(x)
то свободный член делится на p
а старший коэффициент делится на q.
Доказательство:
![]() по
условию. Обе части этого выражения
умножим на
по
условию. Обе части этого выражения
умножим на ![]()
![]()
/…СБ4/
2 часть доказательства
![]()
Левая часть делится на q![]()
![]() .
.
Если старший член равен 1 (нормированный) то все рациональные корни этого многочлена являются целыми числами причем делителями свободного член
![]() ,
,![]() ,
,
![]()
![]() ,
cследовательно корень
целый.
,
cследовательно корень
целый.
Т2: Если рациональное число
![]() где p,q
взаимно простые является
где p,q
взаимно простые является
корнем многочлена f(x)
то для любого целого числа k:
![]()
применима теорему о делении ![]()
Доказательство:
![]()
![]()
![]()
![]()
![]()
![]()
Если предположить, что (![]()
Получаем, что наша дробь сократима, что
противоречит нашему условию. Мы пришли
к тому, что ![]() делится не может следовательно
делится не может следовательно ![]()
■
Следствие: Если многочлен с целыми
коэффициентами нормированный то его
рациональными корнями могут быть только
такие целые числа для которых при любом
![]()
![]()
Доказательство:
![]()
По Т2 ![]()
30 Т(Критерий не приводимости Эйзенштейна):
Если в многочлене с целыми коэффициентами
f(x) коэффициенты
все до старшего делятся на некоторое
простое число p и старший
коэффициент не делится на p
причем ![]() ,
то такой многочлен не приводим над
полем рациональных чисел Q.
,
то такой многочлен не приводим над
полем рациональных чисел Q.
Доказательство:
Пусть эти требования выполняются но многочлен является приводимым то есть представляется в виде произведения:
![]()
![]()
пусть
![]()
![]()
Подставим выражения для ![]() в равенство(2).
в равенство(2).
![]()
![]()
Выполним почвенное умножение в правой части равенства, приведем подобные слагаемые и воспользуемся определением равных многочленов то есть мы приравняем соответствующие коэффициенты:
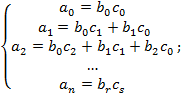
По условию теоремы ![]() Учитывая, что
Учитывая, что ![]() ,
то
,
то ![]() ,
тогда либо
,
тогда либо![]() или либо
или либо ![]() .
По условию
.
По условию ![]() .
Продолжая так и далее получим, что
.
Продолжая так и далее получим, что ![]() от куда следует, что
от куда следует, что ![]() ,
что противоречит условию, что и доказывает
нашу теорему. Заметим, что рассматривая
второй случай также пришли к противоречию.
В этом случае было бы получено, что
,
что противоречит условию, что и доказывает
нашу теорему. Заметим, что рассматривая
второй случай также пришли к противоречию.
В этом случае было бы получено, что
![]() что значит и
что значит и ![]() что противоречит теореме.
что противоречит теореме.
■
Замечание: Из теоремы следует
существование многочленов сколь угодно
большой степени с целыми коэффициентами
не приводимыми над полем Q.
Например ![]() является не приводимым над Q.
является не приводимым над Q.
Пример 1:
Доказать не приводимость многочленов пользуясь критерием Эйзенштейна:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
На полем Q не приводим.
Алгебраические числа.
