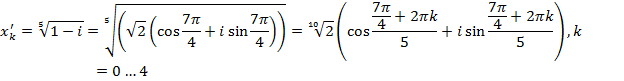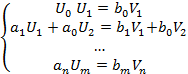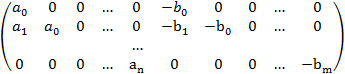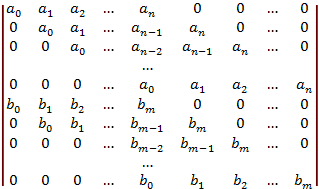§20 (Дополнение к теме нод). Результант 2 многочленов

Алгоритм Евклида позволяет найти НОД и НОК двух многочленов и в частности выяснить являются ли они взаимно простыми. Однако в явном виде алгоритм Евклида не дает условия которому должны удовлетворять коэффициенты 2 многочленов чтобы они были(не были) взаимно простыми. Поставим задачу найти соотношение между коэффициентами 2 многочленов выполнение которого было необходимо и достаточно, что бы многочлены не были взаимно простыми.

Пусть

Найдем

Если они взаимно простыми то их НОД= 1и . Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда

f g не являются взаимно простыми → существуют многочлен что, . Выясним когда такие многочлены существуют. Запишем многочлены:

Подставим многочлены в равенство получим:

На основании определения равенства многочленов приравниваем их соответствующие коэффициенты(таких равенств будет m+n).

Эта система имеет не нулевое решение если определитель равен 0. Для удобства умножим на -1 и транспонируем и его. Этот определитель называют результантом 2 многочленов.

Т1: Многочлены f,g не являются взаимно простыми когда их результант равен 0.

Результант 2 многочленов может быть применен не только для установления взаимной простоты многочленов но и для решения других задач например для исключения переменной из системы 2 алгебраических уравнений с 2 неизвестными.

О) Системой из m алгебраических уровней с n переменными называется система:

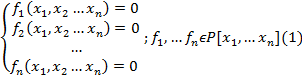
О) Системой 2 алгебраических уравнений с 2 неизвестными называют:

Запишем систему (2) в развернутом виде представив f и как многочлены от одной переменной x из кольца P[y]

Положив получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0:

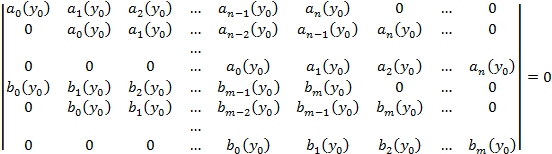
Подставив в (2’), получаем решение и общее решение такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.

Пример 1:

Исключить переменную x и найти решение:

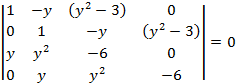
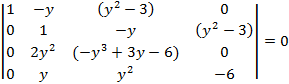
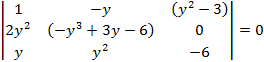
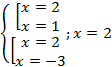
Т3:Многочлены над полем комплексных чисел. Уравнения 3 и 4 степени.

§21 Многочлены над полем комплексных чисел

В предыдущих темах мы изучили многочлены с коэффициентами из произвольного абстрактного поля P. Большое значение имеет рассмотрение многочленов над числовыми полями. Остановимся на С. Среди всех числовых полей поле С состоит в том, что всякий многочлен f(x) степени большей или либо равной 2 является приводимым над полем С то есть разлагается на произведение линейных многочленов по этому его называют замкнутым. Задача разложения над С в произведение линейных членов решается на основании:

Т1(Основная теорема алгебры):

Всякий многочлен положительной степени с числовыми коэффициентами из поля С имеет корень в поле комплексных чисел С.

(Доказана Гауссом в 1799 г. )

Т2: Любой многочлен степени не меньше 2 является приводимым над полем С.

Доказательство:

По Т1 существует ,тогда по теореме Безу: Следовательно даны многочлен раскладывается.

■

Следствие: Чтобы многочлен из С был не приводим над С необходимо и достаточно, что бы степень его была равной 1.

Т3: Многочлен n степени из кольца C[z] раскладывается в произведение линейных множителей, то есть представляется в виде: , где корни.

Доказательство:

На основании теоремы о разложении многочленов в произведение не приводимых множителей запишем, что где не приадимы над C а, каждый не приводимый над С является многочленом 1 степени. Где

Обозначим

таким образом мы доказали что наше разложение существует, причем .

■

Т4: Многочлен n степени в поле С имеет ровно n корней с учетом их кратности.

Пример 1:

Разложить в произведение линейных множителей: