4. Обучение

Для того чтобы можно было начать обучение нашей сети нужно определиться с тем, как измерять качество распознавания. В нашем случае для этого будем использовать самую распространенную в теории нейронных сетей функцию среднеквадратической ошибки (СКО, MSE) [3]: 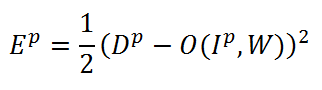В этой формуле Ep — это ошибка распознавания для p-ой обучающей пары, Dp — желаемый выход сети, O(Ip,W) — выход сети, зависящий от p-го входа и весовых коэффициентов W, куда входят ядра свертки, смещения, весовые коэффициенты S- и F- слоев. Задача обучения так настроить веса W, чтобы они для любой обучающей пары (Ip,Dp) давали минимальную ошибку Ep. Чтобы посчитать ошибку для всей обучающей выборки просто берется среднее арифметическое по ошибкам для всех обучающих пар. Такую усредненную ошибку обозначим как E. Для минимизации функции ошибки Ep самыми эффективными являются градиентные методы. Рассмотрим суть градиентных методов на примере простейшего одномерного случая (т.е. когда у нас всего один вес). Если мы разложим в ряд Тейлора функцию ошибки Ep, то получим следующее выражение: Здесь E — все та же функция ошибки, Wc — некоторое начальное значение веса. Из школьной математики мы помним, что для нахождения экстремума функции необходимо взять ее производную и приравнять нулю. 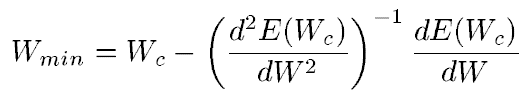Так и поступим, возьмем производную функции ошибки по весам, отбросив члены выше 2го порядка: из этого выражения следует, что вес, при котором значение функции ошибки будет минимальным можно вычислить из следующего выражения: Т.е. оптимальный вес вычисляется как текущий минус производная функции ошибки по весу, деленная на вторую производную функции ошибки. Для многомерного случая (т.е. для матрицы весов) все точно также, только первая производная превращается в градиент (вектор частных производных), а вторая производная превращается в Гессиан (матрицу вторых частных производных). И здесь возможно два варианта. Если мы опустим вторую производную, то получим алгоритм наискорейшего градиентного спуска. Если все же захотим учитывать вторую производную, то обалдеем от того сколько вычислительных ресурсов нам потребуется, чтобы посчитать полный Гессиан, а потом еще и обратить его. Поэтому обычно Гессиан заменяют чем-то более простым. Например, один из самых известных и успешных методов — метод Левенберга-Марквардта (ЛМ) заменяет Гессиан, его аппроксимацией с помощью квадрадного Якобиана. Подробности здесь рассказывать не буду. Но что нам важно знать об этих двух методах, так это то, что алгоритм ЛМ требует обработки всей обучающей выборки, тогда как алгоритм градиентного спуска может работать с каждой отдельно взятой обучающей выборкой. В последнем случае алгоритм называют стохастическим градиентом. Учитывая, что наша база содержит 60 000 обучающих образцов нам больше подходит стохастический градиент. Еще одним преимуществом стохастического градиента является его меньшая подверженность попаданию в локальный минимум по сравнению с ЛМ. Существует также стохастическая модификация алгоритма ЛМ, о которой я, возможно, упомяну позже. Представленные формулы позволяют легко вычислить производную ошибки по весам, находящимся в выходном слое. Вычислить ошибку в скрытых слоях позволяет широко известный в ИИ метод обратного распространения ошибки.