§7. Однорідні лінійні диференціальні рівняння другого порядку із сталими коефіцієнтами

Як уже зазначалося, основною задачею в диференціальних рів­няннях є знаходження їх загального розв'язку. Ця задача найбільш повно вивчена для лінійних диференціальних рівнянь другого поряд­ку із сталими коефіцієнтами, тобто рівнянь виду

(54)

де — сталі дійсні числа, а Q(х) — неперервна функція на дея­кому проміжку (а; b). Для таких рівнянь можна всі розв'язки знайти в квадратурах, а в деяких випадках навіть виразити ці розв'яз­ки через елементарні функції.

Розглянемо спочатку випадок, коли в рівнянні (54)

Т оді рівняння

(55)

називають однорідним диференціальним рівнянням другого порядку.

Знайдемо розв'язок диференціального рівняння (55) методом Ейлера, а саме, у вигляді

(56)

де , — деяке невизначене стале число (дійсне чи комплексне). Знайшовши похідні

і підставивши їх разом з функцією (56) у ліву частину диференціаль­ного рівняння (55)

матимемо

Звідси випливає, що функція (56) е розв'язком диференціального рівняння (55) тоді і тільки тоді, коли многочлен

д орівнює нулю, тобто

(57)

Многочлен називають характеристичним мно­гочленом диференціального рівняння (55), а рівняння (57) — характеристичним рівнянням диференціального рів­няння (55).

Характеристичне рівняння (57) є квадратне рівняння відносно невідомого числа , корені цього рівняння визначаються за формулою

Числа і називають характеристичними чис­лами.

Т оді, як відомо, відносно коренів і можуть бути такі три випадки:

Випадок 1. і е дійсні і різні числа:

Це буде тоді і тільки тоді, коли дискримінант

Диференціальне рівняння (55) при цьому має два різні розв'язки

Побудуємо детермінант Вронського для цих розв'язків:

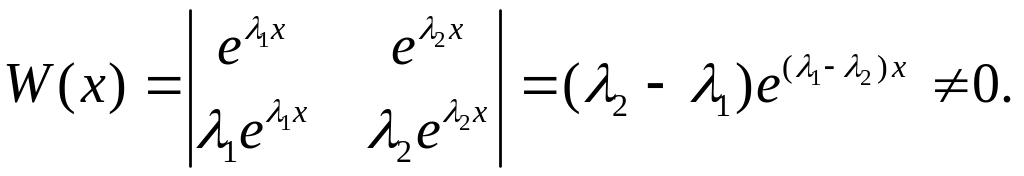
Отже, розв'язки у₁ і у₂ є лінійно незалежні в інтервалі ]—оо; + оо[. Тому функція

(58)

де С₁, С₂ — довільні сталі числа, є загальним розв'язком диферен­ціального рівняння (55).

Випадок 2. Числа і — комплексні. Це буде тоді i тіль­ки тоді, коли дискримінант

Тоді

Позначивши

дістанемо

Отже, корені характеристичного рівняння (57) у випадку 2 є ком­плексно спряжені числа.

Підставивши значення і у формулу (56), матимемо комплекс­ні розв'язки диференціального рівняння (55)

Використовуючи формули Ейлера, перший розв'язок можна запи­сати так:

Позначимо тут дійсну частину через

(60) а уявну частину — через

і доведемо таку лему.

Лема. Функції у₁ = у₁ (х) і у₂ = у₂ (х) є розв'язками диференці­ального рівняння (55).

ПРИКЛАД

Знайти загальний розв'язок диференціального рівняння

Розв'язання. Складемо характеристичне рівняння

О тже,

За формулою (63) загальний розв'язок заданого диференціального рівняння має вигляд

Випадок 3. Числа і рівні, . Це буде тоді і тіль­ки тоді, коли дискримінант

(64)

Д істаємо одне характеристичне число

Отже, диференціальне рівняння (55) має розв'язок

Доведемо, що тоді розв'язком диференціального рівняння (55) є також функція

Справді, знайшовши похідні функції

та врахувавши умову (64), дістаємо

Доведемо, що розв'язки у₁ і у₂ є лінійно незалежні в інтервалі І— оо; + ооІ. Побудуємо детермінант Вронського

Отже, загальний розв'язок рівняння (55) при записується у вигляді

(65) де С₁ і С₂ — довільні сталі числа.