§5. Окремі класи диференціальних рівнянь, що інтегруються в квадратурах або допускають зниження порядку

Диференціальні рівняння порядку п інтегруються в квадратурах дуже рідко. У цьому параграфі ми розглянемо ті класи (типи) диферен­ціальних рівнянь вищих порядків, які можуть бути проінтегровані в квадратурах або порядок яких можна знизити.

Д иференціальне рівняння виду

(20)

де функція / (х) неперервна на відрізку [а; b], інтегрується в квадра­турах. Справді, запишемо його у вигляді

а бо

Т оді (21)

де С₁ — стала інтегрування.

Отже, диференціальне рівняння (20) порядку п ми звели до ди­ференціального рівняння (21) порядку п — 1.

Рівняння (21) запишемо у вигляді

звідки після інтегрування знаходимо

(22)

де С₂ — стала інтегрування.

Я кщо п > 2, то від диференціального рівняння (22) (п — 2)-го порядку переходимо до диференціального рівняння

де С₃ — стала інтегрування, і т. д. Через п кроків дістанемо функцію

яка є загальним розв'язком диференціального рівняння (20).

§6. Лінійні диференціальні рівняння другого порядку.

Розглянемо диференціальне рівняння другого порядку виду

(35)

де і е деякі неперервні функції на відрізку [a;b] (а, b — довільні дійсні числа). Рівняння (35) називається лінійним диференціальним рівнянням другого порядку, а функції — коефіцієнтами заданого рівняння. Припустимо, що для будь-якого x.

Тоді рівняння (35) можна записати у вигляді

(36)

де

Надалі лінійне рівняння розглядатимемо у вигляді (36).

Однорідне рівняння.

Нехай у рівнянні (36) функція . Тоді матимемо рівняння

(37)

Диференціальне рівняння (37) називається однорідним диференціальним рівнянням другого по­рядку.

В ведемо позначення

Тоді диференціальне рівняння (37) можна записати у вигляді

Вираз (38) називається лінійним диференціальним о п ератором другого порядку. Оператор має таку властивість:

де С₁ і С₂ — довільні сталі величини, а у₁ і у₂ — довільні двічі диференційовані функції. Справді, згідно (38), маємо

Користуючись цією властивістю, доведемо таку теорему.

Теорема 1. Якщо функції у₁ = у₁ (х), у₂ = у₂ (х) на деякому проміжку є розв'язками диференціального рівняння (39), то розв'язком цього рівняння е також функція

у = С_іу₁ + С₂у₂, (40)

де С₁ і С₂ — довільні сталі величини.

Д оведення.Згідно з умовою теореми, для будь-якого . . справджуються рівності

Тоді на основі попередньої властивості і цих рівностей маємо

Т еорему доведено.

Виникає запитання: оскільки розв'язок (40) містить дві довільні сталі, то чи буде він загальним розв'язком однорідного рівняння (37)? Щоб відповісти на це запитання, розглянемо такі поняття, як лінійна залежність і лінійна незалежність функцій.

Означення. Функції f_х(х), f₂(х) на проміжку називають­ся лінійно незалежними, якщо тотожність

(41) де — дійсні числа, виконується тоді і тільки тоді, коли

Я кщо існує пара чисел (а₁; а₂), в якій хоча б одне число відмінне від нуля, і справджується тотожність (41), то функції f₁ (x), f₂ (x) називаються залежними на проміжку .

Теорема 2. Якщо функції f_г (х), f₂ (x) диференційовані і лінійнo залежні на проміжку

то детермінант

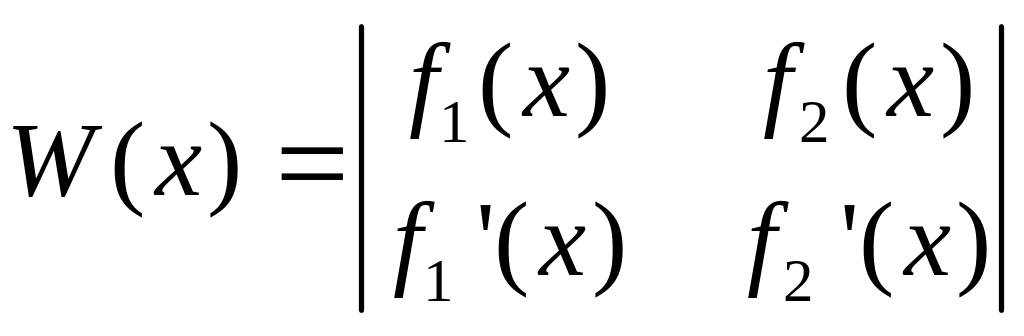
на цьому проміжку дорівнює нулю.

Даний детермінант називається детермінантом В р о н с ь к о г о, побудованого для функцій f₁ (х), f₂ (х).

Д о в е д е н н я. Нехай, наприклад, в тотожності (41) . Тоді

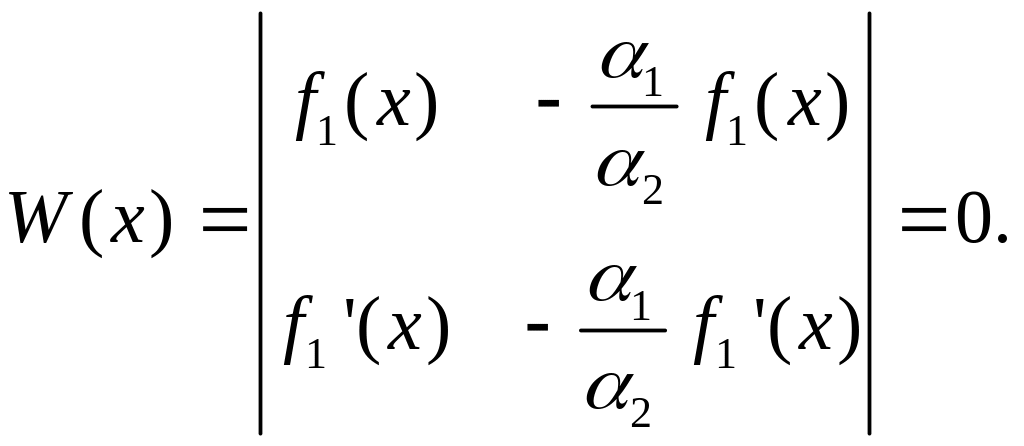
Теорему доведено.

Теорема 3. Якщо функції у₁ = у₁ (х), у₂ =у₂ (х) е розв'яз­ками диференціального рівняння (37) на проміжку і лінійно незалежні на цьому проміжку, то детермінант Вронського, побудо­ваний для цих функцій, в жодній точці проміжку не дорів­нює нулю.

Теорема 4. Для того щоб розв'язки у₁ (х) і у₂ (х) диферен­ціального рівняння (37) були лінійно незалежними на заданому, про­міжку, необхідно і достатньо, щоб детермінант Вронського (42) не дорівнював нулю хоча б в одній точці цього проміжку.

Теорема 5. Якщо розв'язки у₁ (х) і у₂ (х) диференціального рів­няння (37) е лінійно незалежні на розглядуваному проміжку, то функція

у (х) = С_Іy _І (х) + С₂у₂ (х), (46)

де С₁ і С₂ — довільні сталі величини, є загальним розв'язком рівняння (37).

Доведення. Задамо довільні початкові умови

(47) Розглянемо алгебраїчну систему рівнянь

з невідомими С₁ і С₂.

Ця система, згідно з умовою теореми, має єдиний розв'язок

Отже, функція (46), де С₁ і С₂ визначаються останніми форму­лами, і є тим розв'язком диференціального рівняння (37), який за­довольняє довільні початкові умови (47). Тому розв'язок (46) є за­гальним розв'язком диференціального рівняння (37). Теорему до­ведено.

Неоднорідне диференціальне рівняння. Нехай у диференціаль­ному рівнянні (36) функція F(х) тотожно не дорівнює нулю, тобто

Тоді рівняння (36) називається неоднорідним ліній­ним диференціальним рівнянням другого по­ряд к у.

Теорема 6. Якщо функція v = v (х) є розв'язком неоднорід­ного диференціального рівняння (36), а у₁(х) і у₂(х) — лінійно неза­лежні розв'язки однорідного диференціального рівняння (37), то за­гальним розв'язком неоднорідного диференціального рівняння (36) є функція

(49)

де С₁, С₂ — довільні сталі.

ПРИКЛАД

Знайти розв'язок диференціального рівняння

який задовольняє умові

Розв'язання. Знайдемо спочатку загальний розв'язок однорідного рів­няння

Безпосередньою підстановкою впевнюємося, що функції

є розв'язками однорідного рівняння. Побудуємо з цих розв'язків детермінант Вронського:

О тже, розв'язки у₁ і у₂ е лінійно незалежні. Тому загальним розв'язком одно­рідного рівняння (Зі) є функція

де С₁, С₂ — довільні сталі.

Легко бачити, що розв'язком заданого неоднорідного рівняння є функція

v (x) = x.

Тому загальним розв'язком заданого диференціального рівняння є функція

Скористаємось заданими початковими умовами. Матимемо таку систему рівнянь:

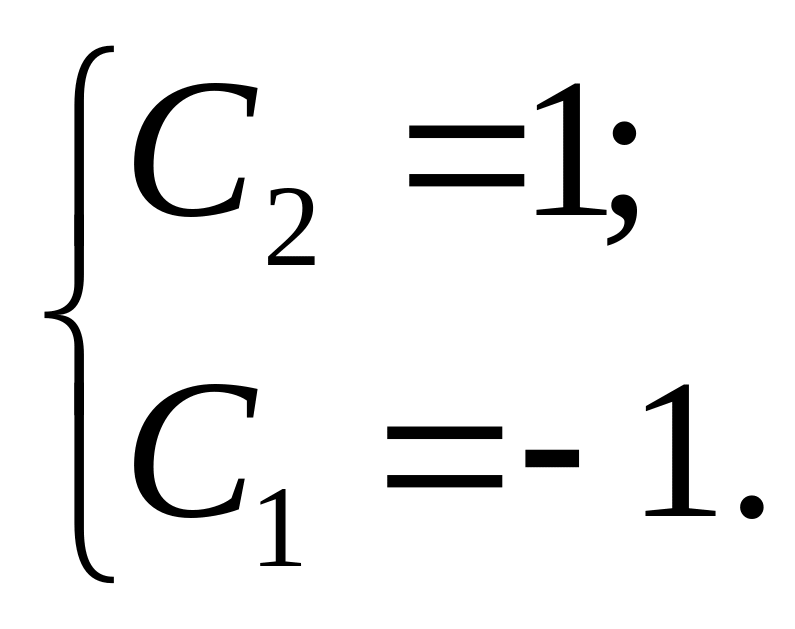
Отже, шуканий розв'язок

Метод варіації довільних сталих. Нехай маємо два лінійно незалежні розв'язки у₁ (х) і у₂ (х) однорідного диференціального рівняння (37) Тоді можна знайти розв'язок неоднорідного диферен­ціального рівняння (36), скориставшись так званим методом ва­ріації довільних сталих (методом Лагранжа) ¹. Роз­глянемо суть цього методу.

Знаходимо розв'язок диференціального рівняння (36) у вигляді

у = С₁ (х) у₁ (х) + С₂ (х) у₂ (х), (51)

де С₁(х) і С₂(х) — невідомі функції. Підберемо ці функції так, щоб функція (51) була розв'язком рівняння (36). Знайдемо похідну

у' = С’₁ (х) у₁ (х) + С’₂ (х) у₂ (х} + С₁ (х) у’₁ (х) + С₂ (х) у₂ (х).

Накладемо на С₁ (х) і С₂ (х) умову, щоб

С’₁ (х) y’₁(х) + С₂ (х) у₂ (х) = 0.

Тоді при виконанні цієї умови

Знайдемо другу похідну

Підставивши значення у, у', у" в диференціальне рівняння (36), дістанемо

Проте у₁ (х), у₂ (х) — розв'язки рівняння (37). Тому

L (у₁) = 0, L (у₂) = 0

і останнє співвідношення набирає вигляду

Отже, якщо функція (51) є розв'язком рівняння (36), то невідомі функції С₁ (х) і С₂ (х) повинні задовольняти таку систему рівнянь:

У цій системі невідомими є похідні С₁(х) і С₂(х). Оскільки детермінант цієї системи

детермінант Вронського, а у₁ (х), у₂ (х) за нашим припущенням є лінійно незалежні розв'язки однорідного рівняння (37), то в жодній точці розглядуваного проміжку.

Тому система має єдиний розв'язок відносно і

де і — відомі функції:

Отже,

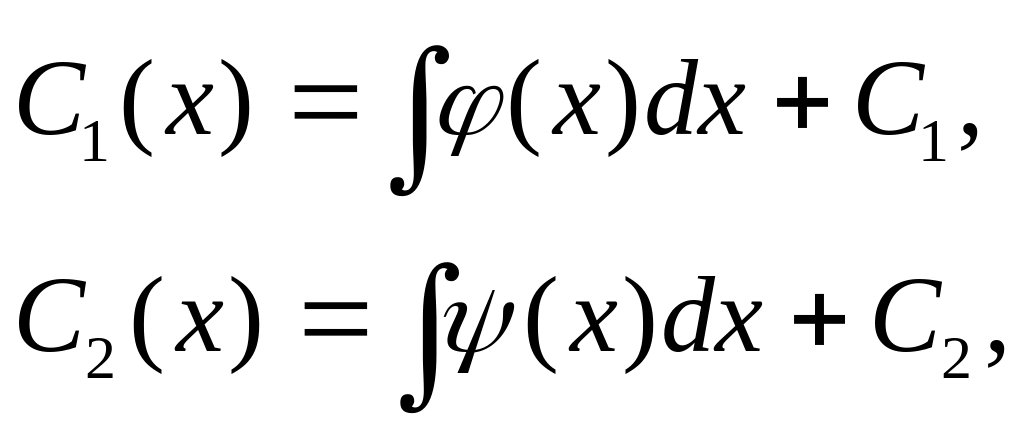
де С₁ і С₂ — сталі інтегрування.

Підставивши значення С₁ (х), С₂ (x:) в співвідношення (51), діста­немо розв'язок рівняння (36)

Оскільки у виразі (52) сума перших двох доданків є загальним розв'язком однорідного диференціального рівняння (37), то функція (52) е загальним розв'язком неоднорідного диференціального рівняння (36), а функція

( 53)

є окремим розв'язком рівняння (36).