
- •Глава 1. Функция нескольких переменных §1. Основные понятия
- •§2. Частные производные
- •§3. Дифференциал функции двух переменных
- •§4. Производная по направлению.
- •§5. Экстремум функции двух переменных.
- •§6. Метод наименьших квадратов
- •Глава 2.Неопределенные интегралы. §1 Основные определения.
- •§2 Основные свойства и таблица интегралов.
- •Глава 3 Основные методы интегрирования. §1.Интегрирование подстановкой
- •§2.Интегрирование по частям
- •§3.Интегрирование рациональных алгебраических функций:
- •§4.Интегрирование тригонометрических функций
- •Глава 4. Определенный интеграл
- •§1. Определенный интеграл как функция верхнего предела
- •§2. Несобственные интегралы с бесконечными пределами
- •§3.Сведения из истории о происхождении терминов и обозначений
- •§4. Поверхность тела вращения.
- •§5. Численное интегрирование.
- •Формула парабол ( формула Симпсона )
§3.Интегрирование рациональных алгебраических функций:
Важнейшим
классом элементарных
функций, интеграл от которых находится
при помощи достаточно простой
последовательности действий, является
класс рациональных функций. Всякая
рациональная функция R
(x)
может быть представлена в виде дроби
![]() ,
где Р (х) и Q
(x)
– многочлены:
,
где Р (х) и Q
(x)
– многочлены:
R (x) = .
Выполним интегрирование дробно-рациональной функции.
Прежде всего заметим, что если степень m числительна Р (х) больше или равна степени n знаменателя Q (x), то, разделив многочлен P (x) на многочлен Q (x), получим целую часть N (x) и в остатке многочлен Р1 (х) не выше (n – 1) – й степени, следовательно:
= N
(x)
+
![]()
Интегрирование многочлена N (x) не доставляет никаких затруднений, и значит, весь вопрос в интегрировании дроби, степень числителя которой меньше степени знаменателя.
Итак, пусть m > n. Такую рациональную дробь иногда называют правильной.
Разложение на простейшие дроби. Мы предполагаем, что многочлены Р (х) и Q (x) имеют действительные коэффициенты, причём коэффициент многочлена Q (x) при хn равен 1 (этого всегда можно достигнуть делением числителя и знаменателя на коэффициент при хn).
Многочлен Q (x) – знаменатель заданной подынтегральной рациональной дроби – может быть представлен, как известно из алгебры, в виде произведения линейных и квадратных множителей с действительными коэффициентами:
Q (x) = (x – a)k … (k2 + px + q)t …,
где а есть k – кратный действительный корень уравнения Q (x) = 0, а квадратное уравнение x2 + px + q = 0 имеет сопряжённые комплексные корни (и значит, p2 – 4q < 0), которые служат t – кратными сопряжёнными комплексными корнями уравнения Q (x) = 0). Интегрирование рациональной дроби мы основываем на знании размножения многочлена на действительные множители (или, что равносильно этому, на знании всех корней уравнения Q (x) = 0). Задачей отыскания корней алгебраического уравнения Q (x) = 0 мы здесь специально заниматься не будем и в последующем полагаем, что корни так или иначе являются известными. При этом оказывается, что дробь можно представить в виде суммы так называемых простейших дробей 1-го и 2-го видов:
![]() ,
,
![]() ,
,
где
![]() – постоянные.
– постоянные.
Каждому множителю (х – а)k в представлении знаменателя Q (x) в разложении дроби на слагаемые соответствует сумма k простейших дробей 1-го вида:
![]()
а каждому множителю (x2 + px + q)t соответствует сумма t простейших дробей 2-го вида:
![]()
Доказывать это предложение в общем случае мы не будем; на подробно рассматриваемых примерах будет видно, так можно фактически осуществить разложение заданной дроби на простейшие дроби, т.е. найти коэффициенты Ak, Ak-1, …, A2, A1, Bt, Ct, Bt-1, Ct-1, …, B2, C2, B1, C1.
Таким образом, при разложении знаменателя Q (x) на множители имеет место разложения дроби на слагаемые:
![]()
+…
Отсюда следует, что интеграл от всякой рациональной дроби сводится к интегралам от простейших рациональных дробей 1-го и 2-го видов, а эти интегралы находятся совсем без труда, что мы и увидим опять-таки на нижеследующих примерах. Эти примеры необходимо разобрать основательно, ибо на них мы демонстрируем, избегая общих рассмотрений, возможные случаи интегрирования рациональных дробей.
Итак, предполагаемый метод интегрирования рациональных дробей состоит в том, что, мы составляем разложение дроби и данный интеграл заменяем суммой интегралов от соответствующих простейших дробей.
Примеры:
1).
![]() Разложение подынтегральной дроби на
простейшие дроби должно иметь вид
Разложение подынтегральной дроби на
простейшие дроби должно иметь вид
![]() =
=
![]() =
=
![]() +
+
![]() +
+
![]()
(какими буквами обозначены коэффициенты, не имеет, конечно, никакого значения). Прежде всего нам нужно найти коэффициенты А, В, С.
Освобождаясь от знаменателей, получим:
x-3 = A (x2 – 1) + Bx (x + 1) + Cx (x – 1).
Так как это тождество, то коэффициенты при одинаковых степенях х должны быть равны между собой:
0 = А + В + С, 1 = В- С, -В = -А.
Из этой системы трёх уравнений с тремя неизвестными находим:
А = 3, В = -1, С = -2.
Ещё проще для определения коэффициентов А, В, и С поступить так: полагая последовательно х = 0, х = 1, х = -1, получим:
-3 = -А, -2 = 2В, -4 = 2С, т.е. снова
А = 3, В = -1, С = -2.
Итак, тождественно
=
![]() -
-
![]() -
-
![]() ,
поэтому
,
поэтому
=
3∫![]() - ∫
- ∫![]() -2∫
-2∫![]() = 3 ln
|x|
- ln
|x
– 1| - 2 ln
|x
+ 1| + C
=
= 3 ln
|x|
- ln
|x
– 1| - 2 ln
|x
+ 1| + C
=
=
 + C.
+ C.
2)
![]()
![]() .
Разложим знаменатель подынтегральной
дроби на множители. Замечая, что он
обращается в нуль при х = -1, разделим его
на х + 1; в частном получится х2
– 4х + 4 = (х – 2)2,
и значит разложение дроби на простейшие
должно иметь вид
.
Разложим знаменатель подынтегральной
дроби на множители. Замечая, что он
обращается в нуль при х = -1, разделим его
на х + 1; в частном получится х2
– 4х + 4 = (х – 2)2,
и значит разложение дроби на простейшие
должно иметь вид
![]() =
=
![]() =
=
![]() +
+
![]() +
+
![]() .
.
Найдем коэффициенты А, В, С. Приводя к общему знаменателю и освобождаясь от него, получим:
х – 5 = А (х – 2)2 + В (х + 1) + С (х + 1) (х – 2).
Здесь удобно положить х = -1, х = 2, х = 0; получаем:
-6 = 9А, -3 + 3В, -5 + 4А + В – 2С
Отсюда:
А
= -![]() ,
В = -1, С =
.
,
В = -1, С =
.
Следовательно,
= -
![]() -
-
![]() +
+
![]() =
=
-
ln
|x
+ 1| +
![]() +
ln
|x
– 2| + C
=
+
ln
|
+
ln
|x
– 2| + C
=
+
ln
|![]() |
+С.
|
+С.
3)
![]() .
Знаменатель легко раскладывается на
множители:
.
Знаменатель легко раскладывается на
множители:
х4 + х3 – х – 1 = х3 (х + 1) – (х + 1) = (х + 1) (х3 – 1) = (х + 1) (х – 1) (х2 + х + 1).
Разложим подынтегральную функцию на простейшие:
![]() =
=
![]() =
+
=
+
![]() +
+![]()
Коэффициенты А, В, C, D находим из тождества
12 = А (х – 1) (х2 + х + 1) + В (х + 1) (х2 + х + 1) + (Сх + D) (x + 1) (x – 1).
Подставляем сюда четыре различных численных значений х, например: х = 1, х = -1, х = 0, х = 2, - получаем систему
12 = 6В, 12 = -А + В – D,
12 = -2A, 12 = 7A + 21B + 3 (2C + D),
из которой находим:
А = -6, В = 2, с = 4, D = -4.
Следовательно,
= -6 ∫
+2
∫![]() + 4 ∫
+ 4 ∫![]() .
.
Последний интеграл в правой части находим, выделяя в числителе производную знаменателя:
∫
=
![]() ∫
∫![]() =
∫
=
∫![]() -
-
![]() ∫
∫![]() =
ln
(x2
+ x
+1) -
∫
=
ln
(x2
+ x
+1) -
∫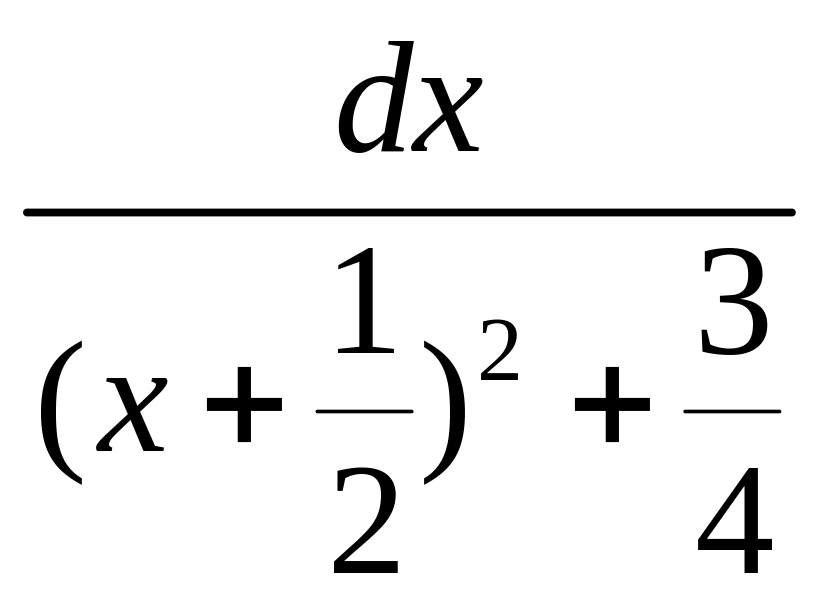 =
ln
(x2
+ x
+1) -
=
ln
(x2
+ x
+1) -
![]() arctg
arctg
![]() + C.
+ C.
Окончательно: =
=
-6 ln
|x
+ 1| + 2 ln
|x
– 1| + 2 ln
(x2
+ x
+ 1) - 4![]() arctg
arctg
![]() +
C
=
+
C
=
=ln![]() + 2 ln (x2
+ x + 1) - 4
arctg
+
C.
+ 2 ln (x2
+ x + 1) - 4
arctg
+
C.
---------------------
4)
∫![]() .
Знаменатель подынтегральной дроби уже
дан своим разложением на множители.
Имеем:
.
Знаменатель подынтегральной дроби уже
дан своим разложением на множители.
Имеем:
![]() =
=
![]() +
+
![]() +
+![]() ,
,
где постоянные А, В, С, D, E будут найдены из того условия, что это равенство тождественное. Освобождаемся от знаменателей:
х2 + х – 1 = А (х2 + 1)2 + (Bx + С) х + (Dx + E) x (x2 + 1).
Подставим в это равенство пять каких-нибудь частных значений х, например: х = -2, х = -1, х = 0, х = 1, х = 2, - придем к системе из пяти уравнений для нахождения пяти неизвестных:
1 = 25 А – 2 (-2В + С) –10 (-2 D + E),
-1 = 4 A – (-B + c) – 2 (- D + E),
-1 = A,
-1 = 4 A + (B + c) + 2 (D + E),
5 = 25A + 2 (2B + C) + 10 (2D + E).
Решая эту систему, находим: A = -1, D = 2, C = 1, D = 1, E = 0.
Значит, тождественно равны дроби
=
![]() +
+
![]() +
+![]() ,
,
и поэтому
∫ = -∫ + ∫ dx + ∫ dx
Первый и третий интеграл справа уже известны, они равны соответственно
–ln x и ln (x2 + 1).
Специально займемся вторым интегралом:
∫
dx
= ∫![]() dx
+ ∫
dx
+ ∫![]() = -
= -
![]() + ∫
.
+ ∫
.
Последний интеграл в правой части обозначении через I2 (в соответствии с тем, что t = 2):
I2 = ∫
Применим здесь следующий прием. К числителю подынтегрального выражения прибавим и вычтем х2 и разобьём интеграл на два:
I2
= ∫![]() = ∫
= ∫![]() - ∫
- ∫![]() = ∫
= ∫![]() -
∫
;
-
∫
;
Применим интегрирование по частям:

![]() =
dv,
v
=
∫
=
dv,
v
=
∫![]() =
-
=
-
![]() ,
,
x = u du = dx,
получим:
![]() =
=
![]() =
.
=
.
Подставляем выражения для I2, найдем:
I2
=
+
∫![]() ,
,
что можно записать так:
I2 = + I2.
Мы привели интеграл I2 к интегралу I1 – в данном случае уже извесному – того же типа, но показатель степени знаменателя подынтегральной простейшей дроби здесь на единицу меньше. Так как I1 = arctg x, то их получаешь окончательно:
∫![]() = - ln
x
-
+
= - ln
x
-
+
![]() +
arctg
x
+
ln
(x2
+ 1) + C
=
+
arctg
x
+
ln
(x2
+ 1) + C
=
=
![]()
![]() + arctg
x
+ C.
+ arctg
x
+ C.
Легко проверить правильность ответа: производная правой части равна подынтегральной функции.
Рассмотренные четыре примера иллюстрируют четыре возможных случая интегрирования рациональной дроби при помощи разложения её на слагаемые простейшие дроби.
