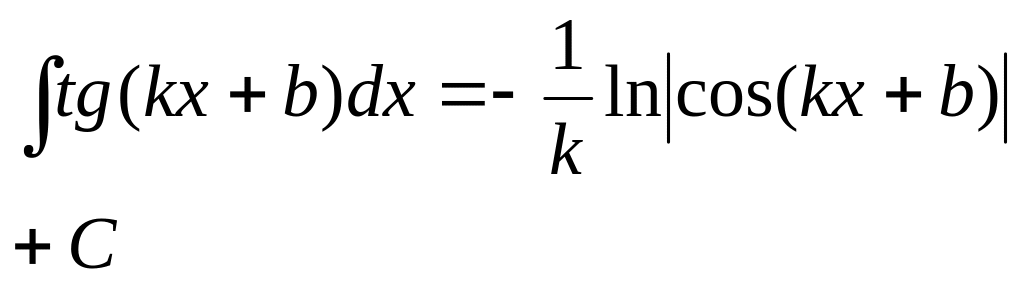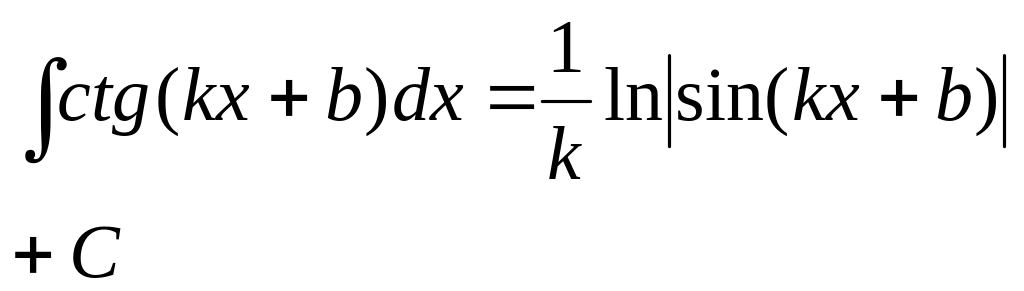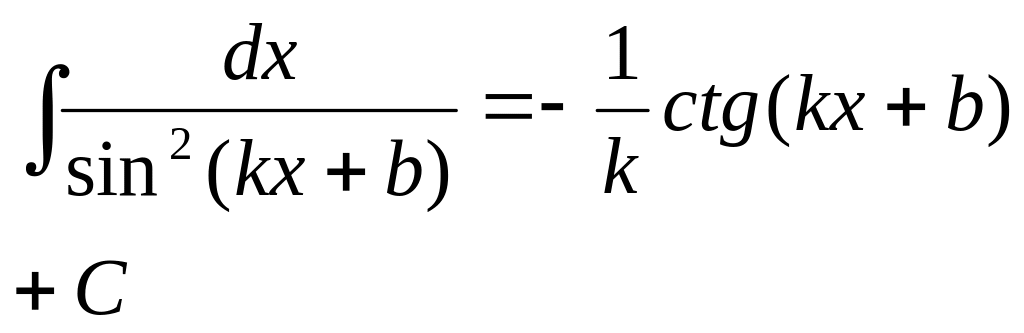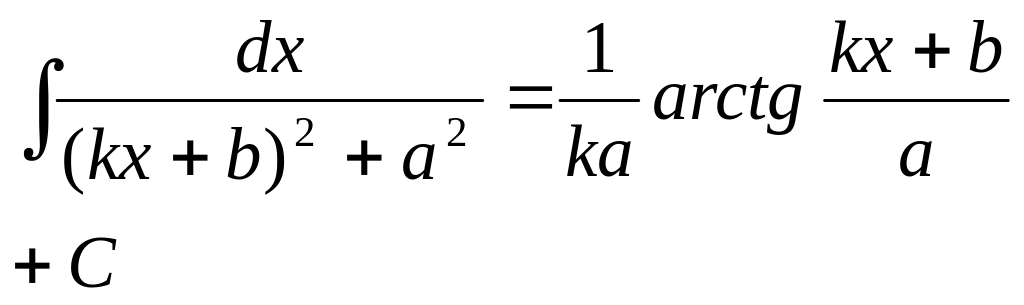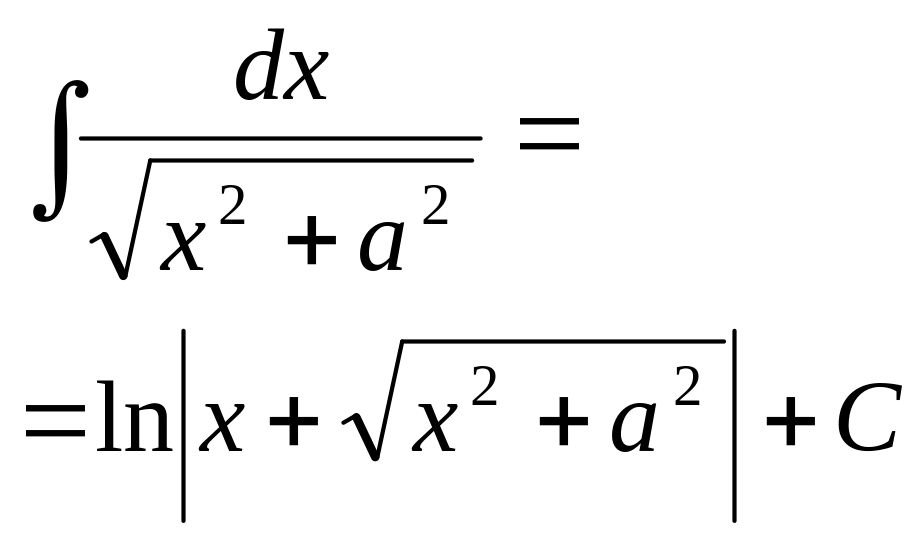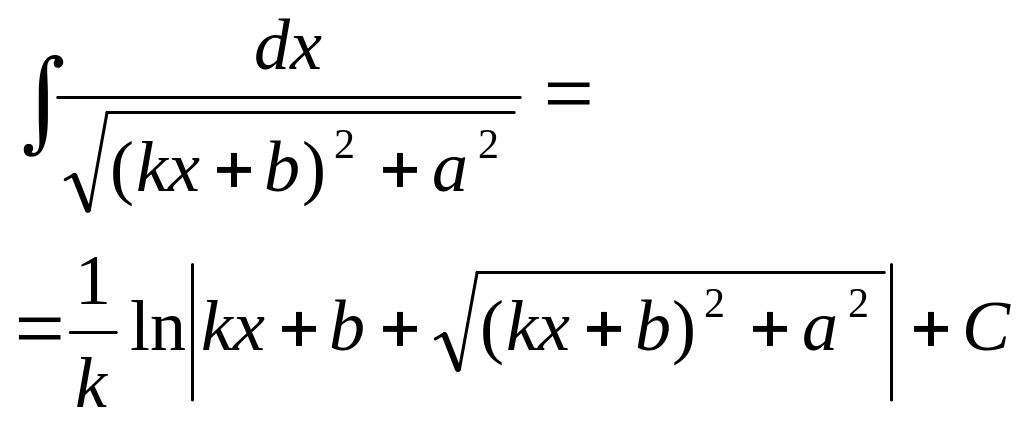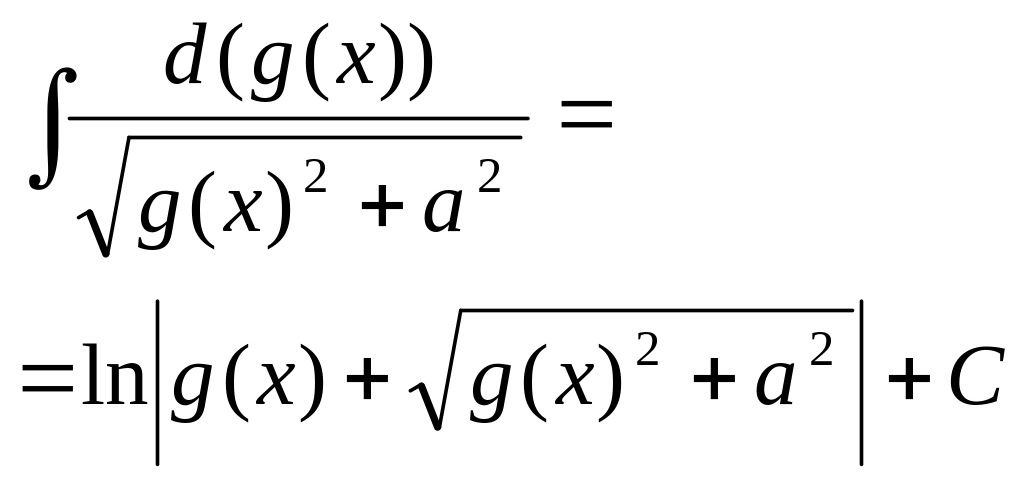Глава 2.Неопределенные интегралы. §1 Основные определения.

Определение: Функция называется первообразной функцией (или просто первообразной) для функции на интервале , если в любой точке интервала функция дифференцируема и имеет производную , равную .

Теорема 1.: Если функции и  любые первообразные для функции на интервале , то всюду на этом интервале , где  некоторая постоянная.

 Положим . Так как каждая из функций и дифференцируема на интервале , то и дифференцируема на интервале , причем всюду на этом интервале .

Из теоремы 12 предыдущей главы если функция дифференцируемая на интервале , и если всюду на этом интервале , то функция является постоянной на интервале . Отсюда 

Следствие. Если  одна из первообразных функций для функции на интервале , то любая первообразная для функции на интервале имеет вид , где  некоторая постоянная.

Определение.: Совокупность всех первообразных функций для функции на интервале называется неопределенным интегралом от функции и обозначается символом:

.

Если  одна из первообразных функций для функции на интервале , то, в силу следствия из теоремы

,

где  некоторая постоянная.

Операцию по нахождению первообразной или неопределенного интеграла называют интегрированием.

§2 Основные свойства и таблица интегралов.

1.

2.

3.

4.

5.

6. - интегрирование по частям

7. - замена переменных

Интегрирование простейших алгебраических дробей.

1.

2.

3.

Основные тригонометрические подстановки.

1. 3. 4.

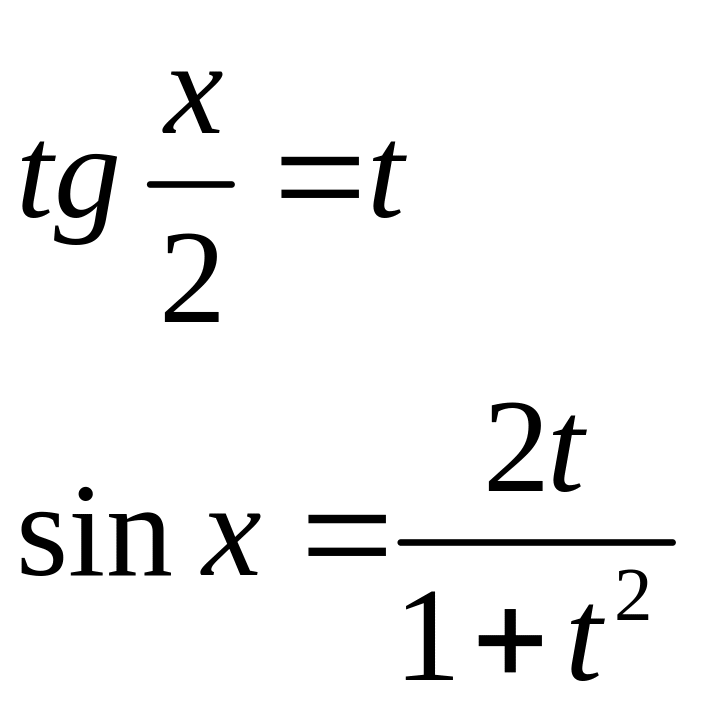
2.

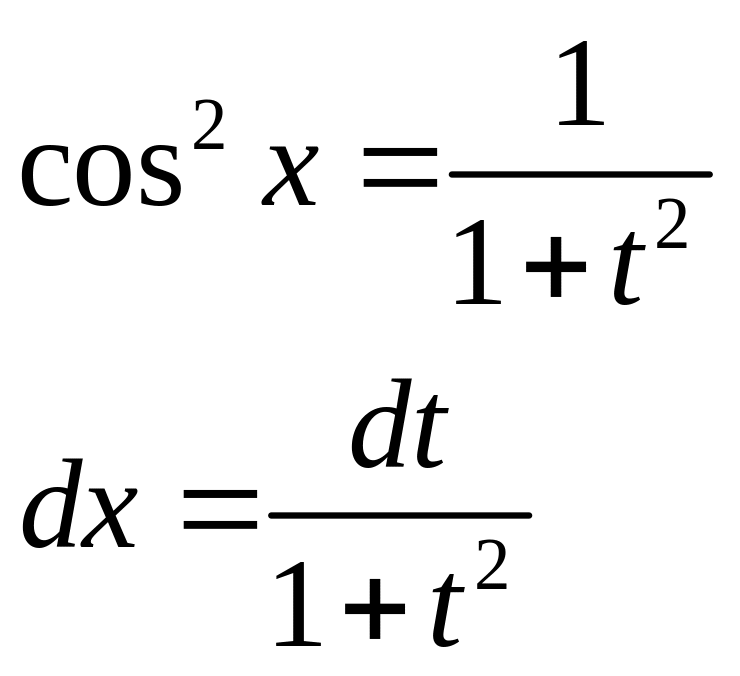
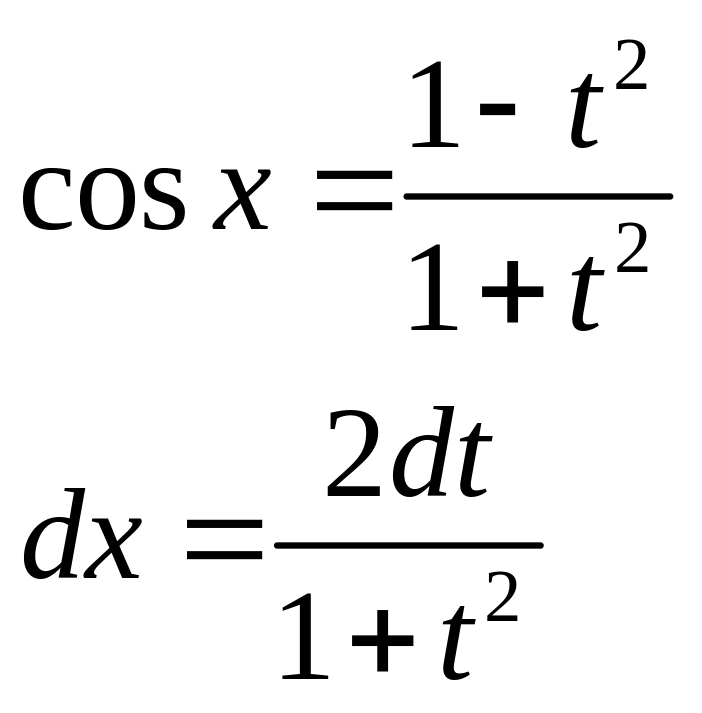
Глава 3 Основные методы интегрирования. §1.Интегрирование подстановкой

Пусть функция определена и дифференцируема на некотором множестве , и пусть  множество всех значений этой функции. Пусть далее для функции существует на множестве первообразная функция , т. е.

.

Тогда всюду на множестве для функции существует первообразная функция, равная , т. е.

.

§2.Интегрирование по частям

Пусть каждая из функций и дифференцируема на множестве и, кроме того, на этом множестве существует первообразная для функции . Тогда на множестве существует первообразная и для функции , причем справедлива формула

,

или в другой форме

.

Первый тип интегралов, берущийся интегрированием по частям:

.

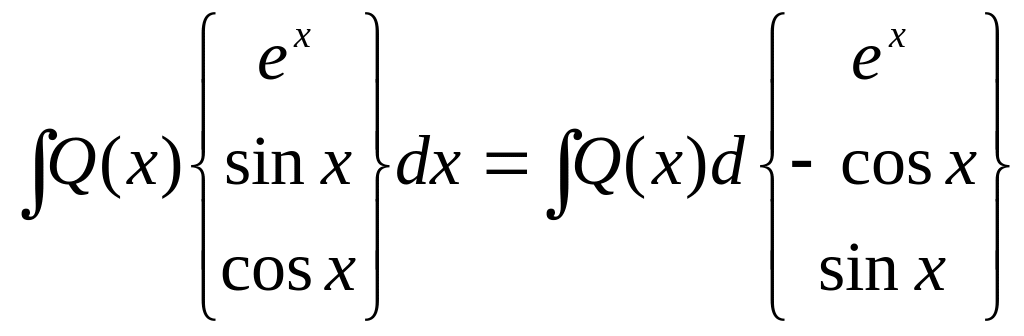Пример: .

Второй тип интегралов, берущийся интегрированием по частям:

.

Пример: .

Пример кругового интеграла: .

Интеграл , берется подстановкой .

Пример: .

Интеграл , берется подстановкой .

Тригонометрические подстановки:

Интеграл , берется подстановкой ,

тогда , , .

Пример: .

Интеграл , берется подстановкой ,

тогда , , .

Пример: .

Интеграл , берется подстановкой ,

тогда , , .

Пример: .

Интегралы от дифференциального бинома .

Берется в трех случаях:

1).  целое, решается разложением

2).  целое, решается заменой , где знаменатель дроби

3)  целое, решается заменой , где знаменатель дроби

Пример:

Интегрирование некоторых трансцендентных функций:

 подстановкой , тогда , .

Пример: .

 подстановкой , тогда , .

Универсальная тригонометрическая подстановка:

 подстановкой , тогда ,

, ,

Пример: .

Если под интегралом и содержатся только в четных степенях, то лучше применять подстановку:

, тогда , , ,