§4. Поверхность тела вращения.

Пусть дана поверхность, образованная вращением кривой y=f(x) вокруг оси Ох.

О 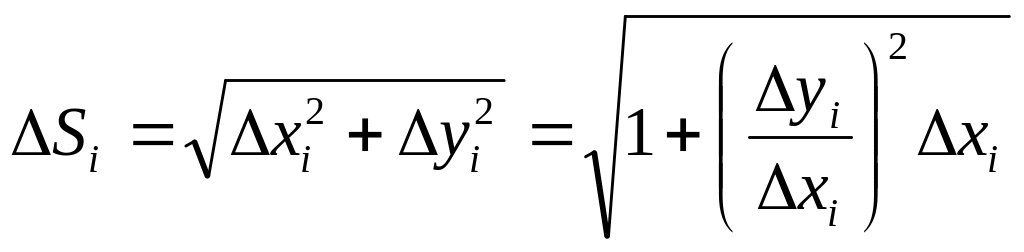пределим площадь этой поверхности на участке а ≤ х ≤ b. Функцию f(x) предположим непрерывной и имеющей непрерывную производную во всех точках отрезка [a;b]. Проведем хорды АМ₁, М₁М₂,….М_n-1B длины которых обозначим через ΔS₁, ΔS₂… ΔS_n (рис. 1). Каждая хорда длины ΔS_i (i=1,2,….n) при вращении опишет усеченный конус, поверхность которого ΔP_i равна:

Применяя теорему Лагранжа получим:

, где Следовательно

Поверхность, описанная ломанной, будет равна сумме

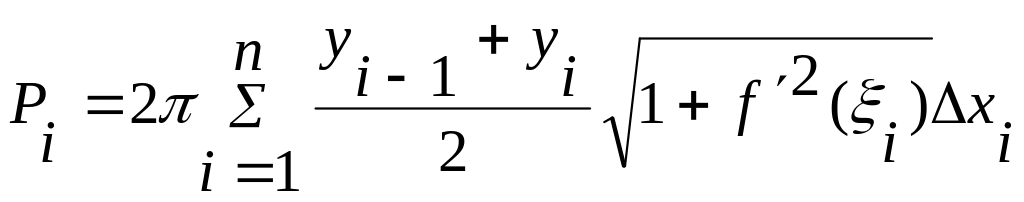
, или сумме

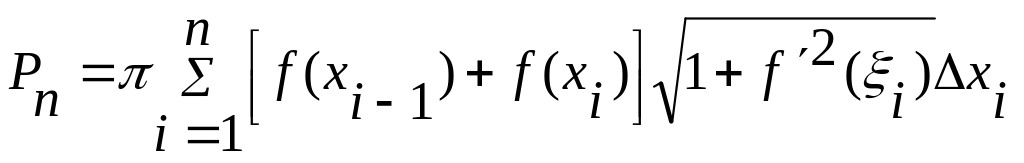, (1)

распространенной на все звенья ломаной. Предел этой суммы, когда наибольшее звено ломаной ΔS_i стремится к нулю, называется площадью, рассматриваемой поверхности вращения. Сумма (1) не является интегральной суммой для функции

( 2), так как в слагаемом, оответствующем отрезку [x_i-1, x_i ], фигурирует несколько точек этого отрезка x_i-1, x_i ,ξ_i.. Но можно доказать, что предел суммы (1) равняется пределу интегральной суммы для функции (2), т.е.

или

(3)

Формула (3) определяет площадь Р поверхности теля вращения возникающего в результате вращения вокруг оси x кривой, заданной на отрезке а ≤ x ≤ b неотрицательной, непрерывно дифференцируемой функцией f(x).

Если вращающаяся кривая задана параметрически: x=φ(t), y=ψ(t) (t₀ ≤ t ≤ t₁) то формула (3) имеет вид,

( 3^/)

§5. Численное интегрирование.

Не для всякой непрерывной функции ее первообразная выражается через элементарные функции. Когда вычисление определенных интегралов по формуле Ньютона – Лейбница затруднительно, применяются различные методы приближенного вычисления определенных интегралов.

І. Формула прямоугольников.

Пусть на отрезке [ a, в ] задана непрерывная функция у = f ( x ). Требуетсявычислить определенный интеграл

в

 f ( x ) d x.

a

Разделим отрезок [ a, в ] точками а = хо, х1, х2… . хп= в на п равных частей длинны ∆х:

∆ х = в – а - шаг деления

п

Обозначим через уо, у1, у2…, уп-1, уп значения функции f ( x ) в точках

хо, х1, х2,…хп, т.е.

уо = f ( xo) ; y1 = f ( x1 )…; yn = f ( xn )

y = f ( x )

yo y1 y2 yn-1 yn

o xo=a x1 x2 xn-1 xn=в

Составим суммы уо ∆ х + у1∆ х + … + уп-1 ∆ х,

у1 ∆ х + у2∆ х + … + уп ∆ х.

Каждая из этих сумм является интегральной суммой для f ( x ) на отрезке

[ a, в ] =>

в п-1

 f ( x ) d x ≈ в – а ( уо + у1 + у2 +… уп-1 ≈ Z yi в – а ; - площадь

а п і=о п

ступенчатой фигуры, составленной из « входящих « прямоугольников «

в n

 f ( x ) d x≈ в – а ( уо + у1 + … уп≈ в – а Z уi - площадь

a n n I-o

ступенчатой фигуры, состоящей из « выходящих « прямоугольников. Это и есть формулы прямоугольников.

Ошибка, совершаемая при вычислении интеграла по формуле прямоугольников, будет тем меньше, чем больше число п ( т.е. чем меньше шаг деления.)

ІІ. Формула трапеций.

Мы получим более точное значение определенного интеграла, если данную кривую y = f ( x ) заменим не ступенчатой линией, а вписанной ломаной. Тогда площадь криволинейной трапеции аАВв заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами АА1, А1А2,…Ап-1В.

Т ак как площадь первой из этих трапеций равна уо + у1 ∆ х, площадь второй равна в 2

у1+ у2 ∆ х и т.д., то  f ( x ) dx ≈ в – а ( уо + уп + у1 + у2+…уп-1 ) ≈

2 a n 2

n-1

≈ в – а ( f ( a ) + f ( в ) + Z fi )

n 2 2 I=1

у

Ап-1 В

А2

А1

А

уо у1 у2 уп-1 уп

о хо=а х1 х2 хп-1 хп=в