Момент силы относительно точки. Плечо силы.
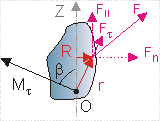
Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.
M. с. относительно центра О наз. векторная величина M0, равная векторному произведению радиуса-вектора r, проведённого из O в точку приложения силы F, на силу M0 = [rF] или в др. обозначениях M0 = r F (рис.). Численно M. с. равен произведению модуля силы на плечо h, т. е. на длину перпендикуляра, опущенного из О на линию действия силы, или удвоенной площади треугольника, построенного на центре O и силе:
Направлен вектор M0 перпендикулярно плоскости, проходящей через O и F. Сторона, куда направляется M0, выбирается условно (M0 - аксиальный вектор). При правой системе координат вектор M0 направляют в ту сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки.
Если система сил имеет равнодействующую, то момент этой равнодействующей относительно любого центра (или оси) равен сумме моментов всех сил системы относительно того же центра (оси) (см. Вариньона теорема). Понятие о M. с. является одним из осн. понятий механики.
ПЛЕЧО СИЛЫ — кратчайшее росстояние от данной точки (центра) до линии действия силы.
Момент силы относительно оси.
M. с. относительно оси z наз. скалярная величина Mz, равная проекции на ось z вектора M. с. относительно любого центра О, взятого на этой оси; величину Mz можно ещё определять как проекцию на плоскость ху, перпендикулярную оси z, площади треугольника OAB или как момент проекции Fxy силы F на плоскость ху, взятый относительно точки пересечения оси z с этой плоскостью. T. о.,
В двух последних выражениях M. с. считается положительным, когда поворот силы Fxy виден с положит. конца оси z против хода часовой стрелки (в правой системе координат). M. с. относительно координатных осей Oxyz могут также вычисляться по аналитич. ф-лам:
где Fx, Fy, Fz - проекции силы F на координатные оси, х, у, z - координаты точки А приложения силы. Величины Mx, My, Mz равны проекциям вектора M0 на координатные оси.
Если система сил имеет равнодействующую, то момент этой равнодействующей относительно любого центра (или оси) равен сумме моментов всех сил системы относительно того же центра (оси) (см. Вариньона теорема). Понятие о M. с. является одним из осн. понятий механики.
Пара сил. Момент пары сил. Теоремы о парах сил.
Пара сил- система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.
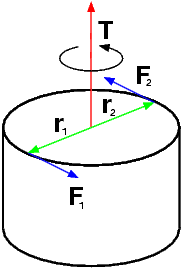
Пара сил не имеет равнодействующей, то есть её действие на тело не может быть механически эквивалентно действию какой-нибудь одной силы; соответственно пару сил нельзя уравновесить одной силой.
Плоскость действия пары – плоскость, проходящая через линии действия пары сил.
Плечо пары- расстояние d между линиями действия пары сил.
Момент пары сил- вектор m, модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.
Моментом пары называется взятое со знаком "плюс" или "минус" произведение модуля сил, образующих пару, на ее плечо. Момент пары сил положителен, если пара стремится вращать тело против часовой стрелки, и отрицателен в противоположном случае. Момент пары определяется по формуле
Важнейшее свойство пары сил выражается теоремой об эквивалентности пар, которую мы приводим без доказательства: все пары сил, лежащие в одной плоскости и имеющие одинаковые по величине и знаку моменты, эквивалентны. Из теоремы следует, что действие пары сил на твердое тело полностью определяется ее моментом. Не изменяя действие пары на твердое тело, мы можем изменять величину, направления и линии действия входящих в нее сил, сохраняя неизменным момент пары. Таким образом, пара сил качественно отличается от простой совокупности двух сил, которые, как мы знаем, можно переносить только вдоль линий действия.
Два других свойства пары сил, необходимые при решении задач:
алгебраическая сумма проекций обеих сил, составляющих пару, на любую ось равна нулю;
алгебраическая сумма моментов обеих сил, составляющих пару, относительно любой точки в плоскости пары равна моменту самой пары.
Пользуясь теоремой об эквивалентности пар, можно доказать теорему о сложении пар: любую систему пар, лежащих в одной плоскости, можно заменить равнодействующей парой, момент которой равен алгебраической сумме моментов слагаемых пар.