24.Плотность распределения вероятностей непрерывной случайной величины. Свойства. График плотности распределения (равномерное распределение).

Опр. Плотностью распределения вероятностей непрерывной случайной величины X называют функцию - первую производную от функции распределения : = 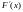. Из этого определения следует, что функция распределения является первообразной для плотности распределения. Свойства. Плотность распределения - неотрицательная функция: .

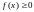Доказательство: Функция распределения – неубывающая функция, следовательно, ее производная = - функция неотрицательная. Геометрически это свойство означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью , либо на этой оси. График плотности распределения называют кривой распределения.

Несобственный интеграл от плотности распределения в пределах от - до равен единице: .

Доказательство: Несобственный интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу . Очевидно, такое событие достоверно, следовательно, вероятность его равна единице. Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью и кривой распределения, равна единице. В частности если все возможные значения случайной величины принадлежат интервалу (a,b), то .

Опр. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Пример. Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину Х, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом, Х имеет равномерное распределение.

Найдем плотность равномерного распределения , считая, что все возможные значения случайной величины заключены в интервале (a,b), на котором функция сохраняет постоянные значения. По условию, Х не принимает значений вне интервала (a,b), поэтому при х<a и x>b. Найдем постоянную С. Так как все возможные значения случайной принадлежат интервалу (a,b), то должно выполнятся соотношение 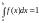, или . Отсюда . Итак, искомая плотность вероятности равномерного распределения

График плотности равномерного распределения изображен на рис.6, а график ф-ии распределения -на 4.

25. Числовые характеристики непрерывных случайных величин. Нормальный закон распределение.

Пусть непрерывная случайная величина X задана плотностью распределения f(х). Допустим, что все возможные значения X принадлежат отрезку [а, b]. Разобьем этот отрезок на п частичных отрезков длиной и выберем в каждом из них произвольную точку x_i (i=1, 2, ..., n). Определим математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений х_{ на вероятности попадания их в интервал (напом­ним, что произведение / (х) Ах приближенно равно вероят­ности попадания X в интервал Ах):

. Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,b], называют определенный интеграл . (*)

Если возможные значения принадлежат всей оси Ох, то .

Предположим, что существует интеграл . Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к , а верхнего - к .

Определим дисперсию непрерывной величины.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку [а, b], то

е сли возможные значения принадлежат всей оси х, том

.

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством .

Замечание 1. Cвойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы

(**)

.

Замечание 3. Математическое ожидание и дисперсия случай­ной величины /?, распределенной равномерно в интервале (0, 1), т. е. если а = 0, b=1, соответственно равны М(R) = 1/2, D(R) =1/12.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Ннормальное распределение определяется двумя параметрами: а есть математическое ожидание, - среднее квадратическое отклонение нормального распределения. Достаточно знать эти параметры, чтобы задать нормальное распределение.

а) По определению математического ожидания непрерывной случайной величины,

.

Введем новую переменную . Отсюда , . Приняв во внимание, что новые пределы интег рирования равны старым, получим

.

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны

Ннормальное распределение определяется двумя параметрами: а есть математическое ожидание, - среднее квадратическое отклонение нормального распределения. Достаточно знать эти параметры, чтобы задать нормальное распределение.

а) По определению математического ожидания непрерывной случайной величины,

.

Введем новую переменную . Отсюда , . Приняв во внимание, что новые пределы интег рирования равны старым, получим

.

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны отн/но начала координат). 2-е из слагаемых равно а

( интеграл Пуассона 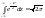). Итак, М (X) = а, т. е. математическое ожидание нормального распределения равно параметру а.

б) По опр/ю дисперсии непрерывной случайной величины, учитывая, что

М(Х) = а, имеем

Введем новую переменную . Отсюда , . Приняв во внимание, что новые пределы интегрирования равны старым, получим

.

Интегрируя по частям, положив и = z, , найдем .

След/но, .

Cреднее квадратич отклонение нормального распределения равно параметру .

Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и ( > 0).

Нормированным называют нормальное распределение с параметрами а =0 и =1.

Замечание 2. Функция F(х) общего нормального распреде­ления

,

а функция нормированного распределения

Функция F₀ (x) табулирована. Легко проверить, что F(х) = F₀ ((х-а)/ ).

Замечание 3. Вероятность попадания нормированной нор­мальной величиныX в интервал (0, х) м/о найти, пользуясь функцией Лапласа .Действительно

.

Замечание 4. Учитывая, что , и, сл/но в силу симметрии относ/но нуля свойство 2), и, след/но, в силу симметрии отн/но нуля

, а значит, и , легко получить, что

Действительно,