1.Предмет ТВ.СВ. Возникновение теории вероятностей относят обычно к XVII веку и связывают с комбинаторными задачами азартных игр. Игры привели к задачам, которые не уклад. в рамки сущ. тогда матем. моделей и привели к введение новых понятий, подходов и идей. Их можно встретить уже у Я. Бернулли, Лапласа, Гаусса и др. XIX – начале XX века стали появляться более серьёзные запросы, которые привели к развитию большого, в значительной мере самостоятельного раздела математики - теорией вероятностей. И ныне она развития. Основной объект теории вероятностей есть случайность или неопределённость, как правило, связанная с незнанием. Примеры: подбрасыванием монеты, где нам трудно учесть те факторы, влияющие на положение монеты после падения. Однако отмеченный парадокс является лишь видимым, попадание в мишень и др . На самом деле точных законов в природе почти не существует. Скажем, классический пример таких законов – закон о зависимости давления газа от его температуры есть на самом деле результат вероятностного характера о числе соударений частиц о стенки сосуда и их скоростях. Большой вероятностью очень малы и не регистрируются нашими приборами. Таким образом, неопределённость стояла в начале процесса познания, она будет стоять и на всём пути его. Эти замечания носят, конечно, общий характер. ТВ следует применять тогда когда будет определяться соотношением между степенью точности, с которой мы хотим изучить данное явление, и сведениями о его природе, которыми мы располагаем.Почти во всех областях человеческой деятельности существуют ситуации, когда те или иные эксперименты или наблюдения могут быть повторены большое число раз в одинаковых условиях. Теорию вероятностей интересуют те эксперименты, результат которых, выраженный каким-либо образом, может меняться от опыта к опыту. События, относящиеся к результату эксперимента, которые при этом могут происходить или не происходить, называют обычно случайными событиями(явления).С.В.При бросании игральной кости могут появиться числа 1, 2, 3, 4, 5 и 6. Наперёд определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная: числа 1, 2, 3, 4, 5 и 6 есть возможные значения этой величины ОПР. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Будем далее обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: x₁,x₂,x₃.Целесообразно различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток. ОПР. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. ОПР. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно. ТВ-эта наука, изучающая закономер случ процессов .Предметом ТВ является изучен вероят закономер массовых однородных СВ

2.Основные понятия тер.вер. Под опытом, экспериментом, исполнением понимается нек-ая воспроизводимая совокупность условий, в к-х наб-ся то или иное явл., пол-ся тот или др.результат. Опыт м/б произведён человеком, явл.природы. При этом если рез-ты опыта изменяются, то говорят об опыте со случайным исходом. Случайным событием наз-ся всякий факт, к-й в опыте со случайным исходом может произойти или не произойти. Случайным называется событие которое при осущ. некоторой совокупности условий могут произойти либо не произойти. Достоверным наз соб , котор обязат произойдет, если будет осуществ определ совокуп услов. Невозмож наз соб, котор заведомо не произойдет , если будет осуществ определ совокуп услов. П-р. 1)Опыт бросания монеты. Событие А-появление «герба»; Событие В-появление «решки»;2)Опыт – воспроизведение 3х выстрелов по мишени. Чтобы оценить взаимность наступления события с ним связывают нек-е число, к-е наз-т вероятностью события А и обозначают Р (А).Свойство Р(О)= 0. А- всегда верное событие, то такое события наз-ся достоверным. и Р(F)=1.Все др.события яв-ся возможными, вероятность любого события возможного б/т заключена между 0 и 1: 0<=Р(А) <=1, А-возможное событие. А- практически не возможное событие, если вероятность этого события близка к 0. Р(А) -~0.В-практически достоверное событие, то Р(В) -~ 1. те элементарные событие в которых наступает событие А наз. Благоприятствующими данному событию. Противоположным событию С наз-ся событие к-е состоит в не появлении события С..П-р.1)Опыт бросания монеты. Событие А- появление «герба»; Событие В-появление «решки». А и В- равновозможные, а следовательно и симметричны. Вероятности их наступления равны –Р(А)=Р(В) (1) ТОГДА события выпадения герба или решки б/т достоверным, они будут определятся равенством: Р(А)+Р(В)=1(2) Из (1),(2) следует Р(А)=1/2; Р(В)=1/2, П-р 2)Опыт бросания игральной кости. Аi- выпадение i-ой грани (выпадение i очков) Сумма i=1 до 6 Р(А)=1; Р(Аi)=Р(Аj), Д/любых i,j=1,6. Р(Аi)=1/6. 1Полнота группы событий. Совокуп.событий в данном опыте образует полную группу, если в рез-те опыта неизбежно д/о появится хотя бы одно из них. Зам.В полную группу м/о добавлять любые невозможные события, полнота группы не меняется. 2Несовместные события. Нес-ко событий в данном опыте наз-ся несовместными, если никакие 2 из них не могут появиться вместе. 3Равновозможные события. Не-ко событий в данном опыте наз-ся равновозможными, если основание считать, что ни одно из них не яв-ся объективно более возможным, чем другое.

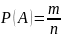где m-число элементарных событий благопр. Событию А, n-число все исход несовместные равновозмож. Образующие полную группу. Формула неприминима1. когда n стрим к ,2. На практике много событий, у которых результат испытания нельзя предоставить в виде совокупности несовмест. Рановозм. Элементар. исходов.

3.Частота и статистическая вероятность событий.Св-ва событий. Если производится серия n опытов, в каждом из которых может появиться событие А, то частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему их числу. Частота случайного события А называется статистической вероятностью. Зам1. Для вычисления частоты события(статистической вероятности) недостаточно знать условия опыта, нужно еще иметь массив статистических данных. Зам2. Частота события - характеристика опытная, экспериментальная, зависит от общего числа проведенных опытов Зам3. По мере увеличения числа n имеет тенденцию приближения к вер-ти события А. При этом приближение достаточно медленно. Зам4. Колебание частоты около в-ти имеет случайный незакономерный характер. Зам5. Частоту случайного события можно рассмотреть как приближенное значение в-ти события А. Поэтому говорят, что случайная величина 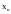сходится по вероятности к величине α, если 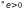, 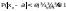1.Правило сложения частот. Если события А и В несовместны, то частота события С={А или В} равна частоте событий А и В. 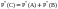Проводится n опытов, событие А произошло m_A событие В-m_B, тогда

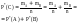
2.Правило умножения. Частота события С ={А или В} равна частоте одного из них, умноженную на “условную” частоту другого, вычисленную в предположении что первое событие имело место

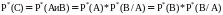
Проводится n опытов, m_A раз производится событие А, из этих m_A раз m_C производится событие В.

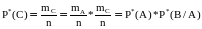
Следствие 1. .

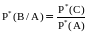Замечание. Весь аппарат теории вероятности построен на понятии частоты события или статистической вероятности события.

4.Пространство элементарных событий. Свойство событий. Пусть производится некоторый опыт со случайным исходом. Обозначим через Ω-множество всех исходов данного опыта. ωЄΩ называется элементарным событием, а Ω-пространством элементарных событий. Если событие А распадается на множество непересекающихся подмножеств, т.е. Тогда 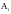называется вариантом события А. Свойства событий. 1.Если события , 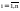таковы, что ∑ образует пространство Ω, то образует полную группу, их сумма есть достоверное событие. 2.События А и В называются несовместными, если они не пересекаются, т.е.А·В={Ø}. 3.События называются попарно несовместными, если появление любого из них исключает появление каждого из остальных.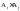 ={Ø},i≠j. 4.Суммой двух событий А и В называется событие С, состоящее в выполнении события А или события В, или обоих событий вместе. 5.Суммой нескольких событий называется событие, состоящее в выполнении хотя бы одного из этих событий. 6.Произведением событий А и В называется событие С, состоящее в выполнении событий А и В. 6.1. Произведением нескольких событий называется событие, состоящее в совместном выполнении всех этих событий. 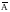7.Противоположным к событию А называется событие , состоящее в не появлении А, а значит, дополняющее А до Ω. 8.Пусть каждое событие А ставится в соответствие число Р(А), называемое вероятностью события А. Потребуем, чтобы вероятность событий удовлетворял следующим аксиомам А)0≤Р(А)≤1 Б)если А и В несовместны, то Р(А+В)=Р(А)+Р(В). Или, если -попарно несовместные, то 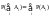. В)Если имеется счетное множество несовместных событий , i=1,2,…, 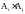={Ø},тогда

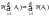
5. Классическое определение вероятности. Аксиомы, определяющие вероят-ть Вероятность-одно из основных понятий ТВ(теор.вероят). Существует несколько опр. этого понятия. пр.1: Пусть в урне содержится 6 оди­нак, тщательно перемешанных шаров, причем 2 из них — красные, 3—синие и 1—белый. Очевидно, возмож­ность вынуть наудачу из урны цветной (т, е. кр. или син.) шар больше, чем возможность извлечь бел. шар. М/о ли охарактеризовать эту возможность числом? Можно. Это число и наз-ют вероят-тью событ. (появления цв. шара). ОПР(классич.):вероятность есть число, характеризующее степень, воз­можности появления события. Поставим задачу: дать количественную оценку возможности того, что взятый наудачу шар цв. Появление цв. шара будем рассм-ть в качестве событ. А. Каждый из возможных рез-ов испытания (испытание состоит в извлечении шара из урны) назовем элем. исходом (элем. событием). Элем. исходы обоз. ч/з ω₁,ω₂,ω₃ и т. д. В пр. возможны следующие 6 эле­м. исходов: ω₁-появ. бел. шар; ω₂,ω₃-появ. кр. шар; ω₄,ω₅,ω₆-синий шар. Эти исходы образуют полную группу попарно несовместных событий (обяз. появится т/о один шар) и они равновозможны (шар вынимают наудачу, шары одинаковы и перемешаны). Те элем. исходы, в кот-ых интересующее нас событие наступает, назовем благоприятствующими этому событию. В пр. благоприятствуют со­быт А (появ. цв. шара) следующие 5 исхо­дов: ω₂,ω₃,ω₄,ω₅,ω₆. Т.о., событ. А набл-ся, если в испы­тании наступает один, безразлично какой, из элем. исходов, благоприятствующих А; в пр. А наблюдается, если наступит ω₂, или ω₃, или ω_4, или ω₅, или ω₆. В этом смысле событие А подразделяется на несколько элем.событий (ω₂,ω₃,ω₄,ω₅,ω₆); элем-ое событие не подразделяется на др. события. В этом состоит различие м/у событием А и элем. событием (элем. исходом). Отнош-ие числа благоприятствующих событ. А эле­м. исходов к их общему числу наз-ют вероят­-тью событ. А и обоз. ч/з Р(А). В пр. всего элем. исходов 6; из них 5 благоприятствуют событ. А. След-но, вероят­-ть того, что взятый шар окажется цв., равна Р(А)= 5/6. Это число и дает количественную оценку ст. возможности появ. цв. шара. Вероят-тью событ. А наз-ют отнош. числа благоприятствующих этому событ. исходов к общ. числу всех равновозможных несовместных элем. исходов, образующих полную группу. Вероят-ть событ. А опред-ся формулой Р(А)=m/n, где т—число элем. исходов, благоприятствую­щих А; п-число всех возможных элем. исходов испытания. Предполагается, что элем. исходы не­совместны, равновозможны и образуют полную группу. Из опр. вероятности вытекают следующие ее св-ва: Св-во 1. Вероят-ть достоверного событ. равна единице. Д-во:если событ. достоверно, то каждый элем. исход испытания благоприятствует собы­т. т = п, след-но, Р(А)=m/n= n/n=1. Св-во 2. Вероят-ть невозможного событ. равна нулю. Д-во:если событ. невозможно, то ни один из элем. исходов испытания не благоприятствует событ. т= 0,след-но, Р(А)=m/n= 0/n=0. Св-во3.Вероят-ть случайного событ. есть полож. число, заключенное м/у 0 и 1. Д-во:случайному событ. благоприятствует лишь часть из общ. числа элем. исходов испы­тания. В этом случае 0 < т < п, значит, 0< m/n <1, след-но, 0<Р(А) <1.Чтд Вероят-ть любого событ удовл-ет нерав-ву 0<=Р(А)<=1 Пр2.Пусть в рез-те испытания наступает одно и т/о одно из событ. ω_i (i=1,2,…n). Событ. ω_i наз-ют элем. событиями (элем. исходами). Отс. следует, что событ. попарно несовместны. Мн-во всех элем. событ., кот-ые могут появ. в испытании, наз-ют простр-вом элем. событий Ω, а сами элем. собы­т.-точками простр-ва Ω. Событ. А отождествляют с подмн-вом (простр-ва Ω ), элементы кот-го есть элем. исходы, благоприятствующие А; событие В есть подмн-во Ω , элем. кот-го есть исходы, благоприятствующие В, и т. д. Т.о., мн-во всех со­бытий, кот-ые могут наступить в испытании, есть мн-во всех подмн-тв Ω. Само Ω наступает при любом исходе испытания, поэтому Ω- достоверное событ.; пустое подмн-во простр-ва Ω- невозможное событ. (оно не наступает ни при каком исходе испытания). Элем. событ. выделяются из числа всех событ. тем, что каждое из них содержит т/о один элемент Ω .Каждому элем.исходу ω_i ставят в соответствие поло­ж. число р_i – вероят-ть этого исхода, причем 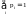. По опр., вероят-ть Р (А) событ. А равна сумме вероят­-тей элем. исходов, благоприятствующих А. Отс. легко получить, что вероят-ть событ. достоверного равна 1, не­возможного-0, произвольного-заключена м/у 0 и 1. Рассм. частный случай, когда все исходы равновозможны. Число исходов равно п, сумма вероят-тей всех исходов равна 1; след-но, вероят-ть каждого исхода равна 1/п. Пусть событ. А благоприятствует m исходов. Вероят-ть событ. А равна сумме вероят-тей исходов, благоприят-их А: Р(А)=1/n+1/n+…+1/n. Учитывая, что число слагаемых равно т, имеем Р(А)=m/n- получили классическое опр. вероят-ти. Построение логически полноценной ТВ основано на аксиоматическом опр. случайного событ. и его вероят-ти.Аксиомы, определяющие вероят-ть: 1.Каждому событ. А поставлено в соот-ие неотриц. действ. число Р (А). Это число наз-ся вероят-тью событ. А. 2.Вероят-ть достоверного событ. равна 1: Р(Ω)=1. 3.Вероят-ть наступления хотя бы одного из попарно несов­местных событ. равна сумме вероят-тей этих событ.

6. Применение комбинаторики при вычислении вероятностей событий. Геометрическое определение вероятности. Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок 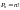, Где n!=1*2*3*…*n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0!=1.

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

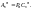
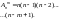
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

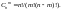
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

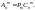
При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А. либо В можно m+n способами..

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А,В) в указанном порядке м/б выбрана mn способами.

Чтобы преодолеть недостаток классического определения вероятности. Состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности - вероятности.

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относи­тельно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством Р = Длина l/Длина L.

Пример 1. На отрезок О А длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков 0В и ВА имеет длину, большую L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине от­резка и не зависит от его расположения на числовой оси.

Решение. Разобьем отрезок О А точками С и D на 3 равные части. Требование задачи будет выполнено, если точка В (х) попа­дет на отрезок СО длины L/3. Искомая вероятность Р= (L/3) L = 1/3.

Пусть плоская фигура g составляет часть плоской фигуры G, На фигуру G наудачу брошена точка. Это означает выполнение следующих предположений: брошен­ная точка может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством Р=Площадь g/Площадь G.

7.Условная вероятность события. Независимость событий (теорема умножения вероятностей для зависимых и независимых событий).Условная вероятность события. Во введении случайное событие определено как событие, которое при осуществлении совокупности условий S может произойти или нет. Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной. Если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события B при дополнительном условии, что произошло событие A. Заметим, что и безусловная вероятность, строго говоря, является условной, поскольку предполагается осуществление условий S. Условной вероятностью P_A(B) называют вероятность события B, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению равна P_A(B)=P(AB)/P(A), P(A)>0 Теорема умножения вероятностей Рассмотрим два события: А и В. Пусть вероятности Р(А) и Р_А(В) известны. Как найти вероятность совмещения этих событий, т е вероятность того, что появится и событие А и событие В. Ответ на этот вопрос дает теорема умножения.Теорема: вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло. Р(АВ)=Р(А)Р_А(В) Док-во: по определению условной вероятности P_A(B)=P(AB)/P(A) Отсюда Р(АВ)=Р(А)Р_А(В) (*) Замечание: применив формулу (*) к событию ВА, получим Р(ВА)=Р(В)Р_В(А) или, поскольку событие ВА не отличается от события АВ, Р(АВ)=Р(В)Р_В(А). (**)Сравнивая (*) и (**), заключаем о справедливости равенства Р(А)Р_А(В)= Р(В)Р_В(А).(***) Следствие: Вероятность совместного появления нескольких событий равна n произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились. Р(А₁А₂А₃…А_n)= Р(А₁)Р_А1(А₂)…Р_А1А2(А₃)…Р_{А1А2..А(n-1)}(A_n) где Р_{А1А2..А(n-1)}(A_n) – вероятность события А_n вычисленная в предположении, что события А_1,А_2,А_3,…,А_n-1 наступили. В частности для трех событий Р(АВС)= Р(А)Р_А(В)Р_АВ(С). Заметим, что порядок, в котором расположены события, может быть выбран любым, т е безразлично какое событие считать первым, вторым и т д. Независимые события. Теорема умножения для независимых событий. Пусть вероятность события В не зависит от появления события А. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т е если условная вероятность события В равна его безусловной вероятности. Р_А(В)=Р(В) (*’)подставим (*’) в (***) предыд.параграфа, получим: Р(А)Р(В)=Р(В) Р_В(А). Отсюда Р_В(А)=Р(А), т е условная вероятность события А в предположении, что наступило событие В, равна его безусловной вероятности. Другими словами, событие А не зависит от события В. Для независимых событий теорема умножения Р(АВ)=Р(А)Р_А(В) имеет вид Р(АВ)=Р(А)Р(В). (**”) т е вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий. Равенство (**’) принимают в качестве определения независимых событий. Несколько событий называют попарно независимыми, если каждые два из них независимы. Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Следствие: Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий Р(А₁А₂…А_n)= Р(А₁)Р(А₂)…Р(А_n) Док-во: рассм-им три события А, В, С равносильно совмещению событий АВ и С, поэтому Р(АВС)= Р(АВ*С). Т.к.события А, В, С независимы в совокупности, то независимы, в частности, события АВ и С, а также А и В. По теореме умножения для двух независимых событий имеем: Р(АВ*С)=Р(АВ)Р(С) и Р(АВ)= Р(А)Р(В). Итак, окончательно получаем Р(АВС)-Р(А)Р(В)Р(С).

8. Формула полной вероятностиПусть событие А может наступить при условии появления одного из несовместных событий В₁,В₂ . . ., Bn, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности Р_B1(A),Р_B2(А)..., Р_Bn(А) события А. Как найти вероятность события А? Ответ на этот вопрос дает следующая теорема.;Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B_l В₂ ..., В_п образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероят­ность события А: Эту формулу называют «формулой полной вероятности».Док-во.По условию, событие А может наступить, если наступит одно из несовместных событий B_l, В₂,..., В_п. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В₁А_, В₂А,..., В_пА. Пользуясь для вычисления вероятности события А теоремой сложения, получим 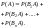(*) Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем 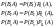Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности

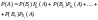
Зам.ФПВприм-ся в случаях когда опыт со случайным исходом распадается на 2этапа: на 1опыте разыгрывается условие; на 2опыте-результат опыта.

9.Теорема гипотез(Формулы Байеса).

Пусть событие А может наступить при условии появления одного из несовместных событий B₁,B₂,…,B_n образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности: P(A)=P(B₁)P_B1(A)+ P(B₂)P_B2(A)+…+ P(B_n)P_Bn(A) (*) Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменилось (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности P_A(B₁), P_A(B₂), … , P_A(B_n). Найдём сначала условную вероятность P_A(B₁),. По теореме умножения имеем P(AB₁)=P(A)P_A(B₁)=P(B₁)P_B1(A) Отсюда P_A(B₁)=[P(B₁)P_B1(A)]/P(A) Заменив здесь P(A) по формуле (*), получим P_A(B₁)=[P(B₁)P_B1(A)]/[ P(A)=P(B₁)P_B1(A)+ P(B₂)P_B2(A)+…+ P(B_n)P_Bn(A)] Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы B_j(j=1, 2, ... , n) может быть вычислена по формуле P_A(B_j)=[P(B_j)P_Bj(A)]/[ P(A)=P(B₁)P_B1(A)+ P(B₂)P_B2(A)+…+ P(B_n)P_Bn(A)] Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

10.Формула Бернули. Локальная теорема Лапласа. Формула Бернулли Если произв-ся неск-ко испытаний, при­чем вер-ть соб-ия А в каждом испыт-ии не за­висит от исходов др-их испыт-ий, то такие испыт-ия наз-ют независимыми относительно события А.В разных независ-ых испыт-ях соб-ие А может иметь либо разл-ые вер-ти, либо 1-у и ту же вер-ть. Будем далее рассм-ть лишь такие независ-ые испыт-ия, в кот-ых соб-ие А имеет 1-у и ту же вер-ть.Ниже восп-ся пон-ем сложного события, по­нимая под ним совмещение неск-их отд-ых соб-ий, кот-ые наз-ют простыми.Пусть производится п независ-ых испыт-ий, в каж­дом из кот-ых соб-ие А может появ-ся либо не появ-ся. Условимся считать, что вер-ть соб-ия А в каждом испыт-ии 1-а и та же, а именно = р. След-но, вер-ть ненаступл-ия со­б-ия А в каждом испыт-ии также пост-на и равна q=1 - p.Пост-им перед собой задачу вычислить вер-ть того, что при п испыт-ях соб-ие А осущ-ся ровно k раз и, след-но, не осущ-ся (п - k) раз. Важно подч-ть, что не треб-ся, чтобы соб-ие А повтор-сь ровно k раз в определ-ой послед-ти. Н/р, если речь идет о появл-ии соб-ия А 3раза в 4-ех испыт-ях, то возм-ны след-ие сложные соб-ия: 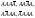. Запись 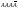означ-ет, что в 1-ом, 2-ом и 3-ем испы­т-ях соб-ие А наступило, а в 4-ом испыт-ии оно не появ-сь, т. е. наступ-о противопол-ое со­б-ие ; соотв-ый смысл имеют и др-ие записи.Искомую вер-ть обозн-им P_n(k). Н/р, символ Р₅(3) означает вер-ть того, что в 5-и испыт-ях соб-ие появ-ся = 3 раза и, след-но, не наступит 2 раза.Поставл-ую зад-у можно решить с помощью так назыв-ой ф-лы Бернулли.

Вывод ф-лы Бернулли. Вер-ть 1-го слож­ного соб-ия, сост-го в том, что в п испыт-ях соб-ие А наступит k раз и не наступит п-k раз, по теореме умн-ия вер-тей независ-ых соб-ий равна 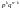. Таких сложных соб-ий может быть ст-ко, ск-ко можно сост-ть сочет-ий из п эле­м-тов по k эл-тов, т.е.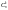 . Т.к. эти сложные соб-ия несовместны, то по теореме слож-ия вер-тей несовместных соб-ий искомая вер-ть = сумме вер-тей всех возм-ых сложных соб-ий. Поск-ку же вер-ти всех этих сложных соб-ий одинаковы, то искомая вер-ть (появл-ия k раз со­б-ияАв п испыт-ях) = вер-ти 1-го сложного соб-ия, умнож-ой на их ч-ло: 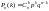или 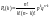. Пол-ую ф-лу наз-ют ф-лой Берн-ли.

Локальная теорема Лапласа.

Выше была выведена ф-ла Бернулли, позво­л-ая вычислить вер-ть того, что соб-ие появ-ся в п испыт-ях = k раз. Легко видеть, что польз-ся ф-лой Берн-ли при больших знач-ях n дост-но трудно, т.к. ф-ла требует вып-ия действий над громадными ч-ми. Н/р, если n=50, k=30, р=0,1, то для отыскания вер-ти 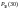надо вычислить выраж-ие Р₅₀(30) =50!/(30!20!)*(0,1)³⁰*(0,9)²⁰, где 50!=30 414093*10⁵⁷, 30!=26525 286*10²⁵, 20!=24329020*10¹¹. Правда, можно неск-ко упростить вычисл-ия, польз-сь спец-ми табл-ми лог-фмов факториалов. Однако и этот путь ост-ся громоздким и к тому же имеет сущ-ый недост-к:табл-ы сод-ат приближ-ые знач-ия лог-мов, поэтому в пр-се вычисл-ий накапл-ся погр-ти; в итоге окончат-ый рез-т может значи­т-но отлич-ся от ист-го.Ест-но возн-ет вопрос: нельзя ли выч-ть интерес-ую нас вер-ть, не прибегая к ф-ле Берн-ли? Оказ-ся, можно. Лок-ая т-ма Лапласа и дает асимптотическую ф-лу, кот-ая позв-ет приближ-но найти вер-ть появл-ия соб-ия = k раз в п испыт-ях, если ч-ло испы­т-ий дост-но велико.Заметим, что для част-го случ., а именно для р = 1/2, асимптотическая ф-ла была найдена в 1730г. Муавром; в 1783г. Лаплас обобщил ф-лу Муавра для произв-го р, отл-го от 0 и 1. Поэтому т-му, о кот-ой здесь идет речь, иногда наз-ют т-мой Муавра - Лапласа.Док-во лок-ой т-мы Лапласа дов-но сложно, поэтому мы приведем лишь формулир-ку т-мы и примеры, иллюстрир-ие ее исп-ние. Локальная теорема Лапласа. Если вер-ть р появ­л-ия соб-ия А в каждом испыт-ии пост-на и отлична от 0 и 1, то вер-ть Р_п (k) того, что соб-ие А появ-ся в n испыт-ях = k раз, прибл-но =(тем точнее, чем больше n)знач-ию ф-ии

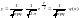
п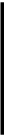 ри x = (k - np)/ .

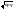Им-ся таб-цы, в кот-ых помещены знач-ия ф-ии 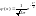, соотв-щие положит-ым знач-ям арг-та х. Для отрицат-ых знач-ий арг-та польз-ся теми же табл-ми, т.к. ф-ия четна, т.е. .

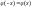Итак, вер-ть того, что соб-ие А появ-ся в п независ-ых испыт-ях = k раз, прибл-но равна 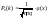где x =(k – np)/ .

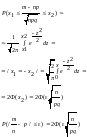
11.Интегральная теорема Лапласа. вероятность отклонения частоты от вероятности в независимых испытаниях.

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом вероятность появления события равна p(0<p<1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна

Замеч1 Ф(-x)=-Ф(x) Замеч2 Ф(x)-по таб знач

Замеч3 xЮ5, Ф(x)≈0.5

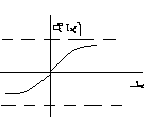
Вероятность отклонения частоты от вероятности в независимых испытаниях.

Опыт: производит n независим испытан, в каждом из которых вероят появлен события А постоянно и равна p=const, 0 <p<1.Найти вероятность того, что отклонен относит частоты m/n, m-число испытан,nчисло благоприят,/m/n-p/< , , 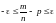, 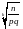q=p-1 вероятность наступ событ А.

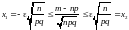
при =0 вероятность совпаден частоты с вероятностью=0.

Пример:Вероят появлен соб а в каждом 10 тыс испытаний (независим) n=10000, равно р=0.05. Найти вер того , относит частота появлен событ А. находится от вероят р не более чем на =0.001.

Решение6 q=0.5 ,

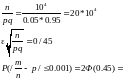
=0.1736*2=0.3472

Если =0.01 то 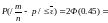2*0.49=0.98

12. Случайные величины (СВ). Дискретные (ДСВ) и непрерывные (НСВ) СВ. Способы задания ДСВ. Закон распределения СВ.Случайной наз-ют величину, которая в результате испытан ия примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.Х: х1, х2, х3, где Х – СВ, а х1, х2, х3 – возможные значения.Дискретной наз-ют СВ, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений ДСВ может быть конечным и бесконечным.Непрерывной наз-ют СВ, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений НСВ бесконечно.Для задания ДСВ недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.Законом распределения ДСВ наз-ют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.При табличном задании закона распределения ДСВ первая строка таблицы содержит возможные значения, а вторая – их вероятности:

Х х₁ х₂ ... х_n

р р₁ p₂ …p_n

В одном испытании СВ принимает одно и только одно возможное значение, следовательно события Х=х₁, Х=х₂, ... , Х=х_n образуют группу; следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице: р₁ + p₂ + … +p_n = 1.Для наглядности закон распределения ДСВ можно изобразить и графически, для чего в прямоугольной системе координат строят точки (х_i, p_i), а затем соединяют их отрезками прямых. Полученную фигуру наз-ют многоугольником распределения.