19. Среднее квадратическое отклонение. Среднее квадратическое отклонение суммы взаимно независимых случайных величин.

Для оценки рассеяния возможных значений слу­чайной величины вокруг ее среднего значения кроме дис­персии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии: Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность совпадает с размерностью X. Поэтому в тех случаях, когда жела­тельно, чтобы оценка рассеяния имела размерность слу­чайной величины, вычисляют среднее квадратическое от­клонение, а не дисперсию. Например, если X выражается в линейных метрах, то будет выражаться также в линейных метрах, a D (X) — в квадратных метрах. Среднее квадратическое отклонение суммы взаимно независимых случайных величин Пусть известны средние квадратические откло­нения нескольких взаимно независимых случайных вели­чин. Как найти среднее квадратическое отклонение суммы этих величин? Ответ на этот вопрос дает следующая Теорема. Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

Доказательство. Обозначим через X сумму рас­сматриваемых взаимно независимых величин:

Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий слагаемых, поэтому

Отсюда , или окончательно

20.Числовые характеристики(мо, дсв,ско) взаимно независимых св. Начальные и центральные моменты. Мо.

Математическое ожидание дискретной величины- это сумма произведении возможных величин на их вероятности, т.е. М(Х)=∑(I от 1 до n)x_ip_i М(Х)= ∑ (I от 1 до ∞)x_ip_i- при сходимости правой части. Пр-р:Найти МО числа появления события А в одном испытании, если вер-сть появления соб-я А равно р. Решение:X: x₁=1 x₂=0; P: p 1-p M(X)=x₁*p+x₂*(1-p)=1*p+0*(1-p)=p+0=p Замечание:МО числа появления события в данном испытании равна вероятности этого события. Св-ва:1°. М(С)=С, где С-const.2°. М(СХ)=СМ(Х), 3°. X,Y-независ СВ, M(XY)=M(X)M(Y) Док-во: X:x₁,x₂,…,x_n; P:p₁,p₂,…,p_n; Y:y₁,y₂,…,y_n; Q:q₁,q₂,…,q_n; XY:x₁y₁;x₁y₂;…; x₁y_n;…; x_ny₁,x_ny₂;;x_ny_nP:p₁q₁;p₁q₂;…;p₁q_n;…;p_nq₁;p_nq₂;…;p_nq_n M(XY)=x₁p₁∑ (j от 1 до m)y_jq_j+…+x_np_n∑ (i от1 до n)y_iq_i=(∑ (i от1 до n)x_ip_i)( ∑ (j от 1 до m)y_jq_j)=M(X)M(Y) ч.т.д Сл-е: Пусть Х_i-независимыеСВ, где i=1,…,n,тогда M(П (i от1 до n )X_i)= П(i от1 до n )M(X_i) 4°.M(X+Y)=M(X)+M(Y) Д-во: M(X+Y)=(x₁+y₁)p₁₁+(x₂+y₂)p₁₂+…= =x₁∑ (i от 1 до n) p_1i+…+ x_n∑ (i от 1 до n)p_ni+ y₁∑ (j от 1 до m)p_1j+…+ y_n∑ (j от 1 до m)p_mj=/∑(j от 1 до m)p_1j=p₁;…/= ∑ (i от1 до n)x_ip_i+ ∑ (j от 1 до m)y_jq_j=M(X)+M(Y) МО числа появлении события А в независимых испытаниях = произведению числа испытаний на вероятность появления события в каждом испытании M(X)=n*p Док-во:при проведении n испытании допустим, что событии в 1 испытании=x₁; во 2 испытании=x₂;…;в n испытании=x_n, тогда X=∑ (i от1 до n)x_i M(X)=M(∑ (i от1 до n)x_i )= ∑ (i от1 до n)M(x_i),M(x_i)=p,M(X)= ∑ (i от1 до n)p=p_n ч.т.д. ДСВ. Дисперсия дискретной СВ- отклонение СВ от ее МО называется СВ и определяется как Х-М(Х) X: x₁,x₂, … ,x_n P: p₁,p₂, … ,p_n X-M(X): x₁-M(X); x₂-M(X);…; x_n-M(X);P:p₁,p₂, … ,p_n МО от отклонения от СВ и его МО=0,т.е. M(X-M(X))=M(X)-M(M(X))=M(X)-M(X)=0

ДСВ, Д(Х)-называют МО от квадрата отклонения ее МО, т.е. Д(Х)=М([X-M(X)]²); [X-M(X)]² : [x₁-M(X)]²;[x₂-M(X)]²;…;[x_n-M(X)]² P: p₁; p₂;… ;p_n;Д(Х)= ∑ (i от1 до n)[x_i-M(X)]²p_i; Д(X)=M(X² 2XM(X)+M²(X))=M(X²)-2M(X)M(X)+M(M²(X))=M(X²)-M²(X), т.е. Д(X)=M(X²)-M²(X) Св-ва:1°Д(С)=M([C-M(C)]²)=M(0-0)=M(0)=0 2°Д(СX)=M((CX)²)-M²(CX)=M(C²X²)-C²M²(X)=C²M(X²)-C²M²(X)=C²[M(X²)-M²(X)]=C² Д(X) 3°Д(X+Y)= Д(X)+ Д(Y) Док-во: Д(X+Y)=M((X+Y)²)-M²(X+Y)= =M(X²+2XY+Y²)-M(X+Y)M(X+Y)= =M(X²)+2M(X)M(Y)+M(Y²)-[M(X)+M(Y)]²=M(X²)+M(Y²)+2M(XY)-M²(X)-2M(X)M(Y)-M²(Y)=M(X²)-M²(X)+M(Y²)-M²(Y)= Д(X)+ Д(Y)

4° Д(X-Y)= Д(X+(-Y))= Д(X)+ Д((-1)Y)= Д(X)+ (-1)²Д(Y)= Д(X)+ Д(Y) Пусть производится n независимых испытаний, вероятность появления события А-const и равно p.X-число появлений события А в n испытаниях. Д(X)-?.x_i-«число» появления события А в i-ом испытании. X=x₁+x₂+…+x_n=∑ (i от 1 до n) x_i Д(X)= ∑ (i от 1 до n) Д(x_i) Д(x_i)=M(x_i²)-M²(x_i) x_i: 0;1 p:1-p;p x_i²: 0;1 M(x_i²)=0(1-p)+1p=0+p=p M(x_i)=p Д(X)=p-p²=p(1-p)=pq,где q=1-p Д(X)=npq СКО. Средним квадратичным отклонением СВ называется квадратный корень из дисперсии этой СВ,т.е. σ=√Д(X) σ(∑ (i от 1 до n)x_i)=√Д(∑ (i от 1 до n)x_i)=√ ∑ (i от 1 до n) Д(x_i)=√ ∑ (i от 1 до n)σ²(x_i)Одинаково распределенные независимые СВ. xi,i=1,…,n x(с чертой)=(1/n) ∑ (i от 1 до n) x_i- среднее арифметическое x_i1. M(х(с чертой))=M((1/n) ∑ (i от 1 до n) x_i)=(1/n) ∑ (i от 1 до n) M(x_i)=/ M(x_i)=m₀(с чертой)/=(1/n)m₀(с чертой)n= m₀(с чертой) 2. Д(х(с чертой))=Д((1/n) ∑ (i от 1 до n) x_i)=(1/n²)Д(∑ (i от 1 до n) x_i)=(1/n²) ∑ (i от 1 до n)Д(x_i)=/Д(x_i)=d₀/=(1/n²)d₀n=d₀/n 3. σ(x(с чертой))=√Д(x(с чертой))=√(d₀/n)=σ₀/√n , σ_0=√ d₀ Начальные и центральные теоретические моменты. Начальным моментом к СВ X наз-ют МО Х в к-ой степени, т.е. ν_к=М(х^к), частные случаи ν₁=М(Х),ν₂=М(Х²) Д(Х)=ν₂-ν₁² Центральным моментом к СВ Х называют МО (X-M(X)) в к-ой степени, т.е. μ_к=M([X-M(X)]^k), частные случаи μ₁=M(X-M(X))=0, μ₂=M([X-M(X)]²)= =Д(Х), μ₂=ν₂-ν₁²,μ₃=ν₃-3ν₂ν₁+2ν₁³,μ₄=ν₄-4ν₃ν₁+6ν₂ν₁²-3ν₁⁴

21.Законы больших чисел. Неравенство и теорема Чебышева (Чебышев Пафнутий Львович (1821 – 1824) – русский математик.) На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение большого числа случайных величин практически утрачивает случайный характер и становится закономерным. Этот факт очень важен на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов. Однако, это возможно только при выполнении некоторых условий, которые определяются законом больших чисел. К законам больших чисел относятся теоремы Чебышева (наиболее общий случай) и теорема Бернулли (простейший случай), которые будут рассмотрены далее. Рассмотрим дискретную случайную величину Х (хотя все сказанное ниже будет справедливо и для непрерывных случайных величин), заданную таблицей распределения:

Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число e.Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше чем .

Теорема Чебышева: если последовательность попарно независимых случайных величин X1,X2…Xn..имеет конечные математ ожидания и дисперсии этих величин равномерно ограничены(не превышают постоянного числа С ) то среднее ариф случайных величин сходится по вероятности к среднему ариф их математ ожиданий, те если –любое положительное число то

В частности, сред ариф послед попарно независим величин, дисперсии которых равномерно ограничены и которые имеют одно и то же матем ожидание а те если – любое положительное число

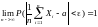
22.Теорема Бернулли. Если в каждом из n независимых испытаний .вероятность р появления события А постоянна то как угодно близка к единице вероятность того, что-отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым если ,число испытаний достаточно велико.

Другими словами» если —сколь угодно малое поло­жительно число, то при соблюдении условий теоремы имеет место равенство

ЗамечаниеВ теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каж­дом испытании.

Таким образом, сходимость относительной частоты т/п к веро­ятности р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности» *>. Точнее, различие между указанными видами сходимости состоит в следующем: если т/п стремится при п—> к р как пределу в смысле обычного анализа, то начиная с некото­рого n= N для всех последующих значений п неуклонно выпол­няется неравенство | т/п—р\ < ; если же т/п стремится по веро­ятности к р при п—> , то .для отдельных значений п неравенство может не выполняться.

Итак, теорема Бернулли утверждает, что при п—> относи­тельная частота стремится по вероятноети к р. Коротко теорему Бернулли записывают так: /

Как видим, теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности

Относительной частотой события наз отношение числа испытан, в которых событие появилось, к общему числу фактич произведенных испытаний.W(A)=m/n

m-число появ события,n-общее число испытаний.А различ опытах относ частоты измен мало, колеблясь около некоторого постоянного числа.Это постоян число есть вероятность появлен событ.

*> Последовательность случайных величин X_lt Х₂, .. сходится по вероятности к случайной величине X, если для любого > 0 вероятность неравенства \Х_п — Х\< при п—> стремится к единице.

23.Функция распределения вероятностей непрерывной СВ. Свойства. График функции распределения.Ф-ией распред-ия наз-ют ф-ию вида F(x), определяющую вероятность того, что случ-ая величина Х в результате испытания примет значение, меньшее х, т.е. F(x)=P(X<x). Случ-ую величину наз-ют непрерывной, если ее ф-ия распределения есть непрерывная, кусочно-дифференцируемая ф-ия с непрерывной производной. 1° Значения ф-ии распределения [0,1]: . Док-во. Св-во вытекает из определения ф-ии распределения как вероятности: вероятность всегда есть неотриц-ое ч-о, не превышающее 1. 2° F(x) –неубывающая ф-ия, т.е. , если . Док-во. Пусть . Событие, состоящее в том, что Х примет значение,< , можно подразделить на =>-ие 2несовместных события: 1)Х примет значение, < , с вероятностью 2)Х примет значение, удовлетворяющее неравенству , с вероятностью . По теореме сложения имеем . => 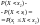или . (*) т.к. 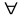вероятность есть число неотриц-ое, то , или . =>1.Вероятность того, что случайная величина примет значение, заключённое в (a,b), = приращению ф-ии распределения на этом интер-ле: 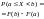(**). (это =>-e вытекает из (*), если 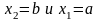) =>2.Вероятность того, что непрерывная случайная величина Х примет одно определённое значение = 0. 3°. Если возможные значения случайной величины , то: 1)F(x)=0 при ; 2)F(x)=1 при . Док-во.1) Пусть 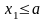, тогда событие невозможно и, => вероятность = 0. 2)Пусть 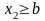, тогда событие достоверно и, => его вероятность = 1. =>. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы =>-ие предельные соотношения: ; . По док-м св-м график расположен в полосе, огран-ой прямыми у=0 и у=1. При возраст-ии ч в (a,b), в к-м заключены все возможные значения случайной вел-ны, график «подымается вверх». При ординаты графика =0; при — 1.