Фундаментальная система решений линейного однородного уравнения

 Определение. Любые   линейно независимых решений линейного однородного дифференциального уравнения -ного порядка называется фундаментальной системой решений этого уравнения.

Из предыдущих теорем сразу следует еще одна важная теорема.

Теорема 7. Решения   уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского  отличен от 0 хотя бы в одной точке .

Доказательство. Равносильная переформулировка утверждения теоремы – решения   линейно зависимы тогда и только тогда, когда  на . Но это утверждение сразу следует из теорем 5 и 6.

Теорема 8. Для любого линейного однородного дифференциального уравнения (2) существует фундаментальная система его решений.

Доказательство. Построим такую фундаментальную систему решений. Для этого возьмем произвольную точку   и поставим  различных задач Коши: .

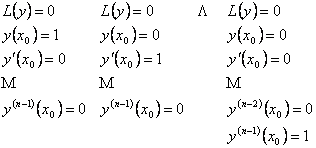По теореме 1 о существовании и единственности у каждой из этих задач имеется решение, и мы обозначим   - решение 1-й задачи,  - решение 2-й задачи, …,  - решение -ной задачи. Мы получили  - решения уравнения (2). Найдем  для этих функций: 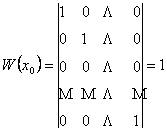. Следовательно, по теореме 7, функции  образуют искомую фундаментальную систему решений уравнения (2).

Теорема 9. Пусть   - фундаментальная система решений уравнения (2). Тогда для любого решения   этого уравнения существуют постоянные  такие, что .

Доказательство. Возьмем произвольную точку  и рассмотрим систему уравнений относительно неизвестных :  (11). Определитель этой системы  не равен 0, т.к.   - фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение . Рассмотрим теперь функцию . По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка  включительно в точке   совпадают со значениями  и ее последовательных производных в точке . По теореме 1 о единственности решения задачи Коши , .

Замечание. Теоремы 8 и 9 означают, что размерность векторного пространства решений уравнения (2) равна , а любая фундаментальная система решений представляет собой базис этого пространства

значениями  и ее последовательных производных в точке . По теореме 1 о единственности решения задачи Коши , .

Замечание. Теоремы 8 и 9 означают, что размерность векторного пространства решений уравнения (2) равна , а любая фундаментальная система решений представляет собой базис этого пространства

Билет №15

Структура общего решения неоднородной системы

Любые n – r линейно независимых решений системы называются ее фундаментальной системой решений.

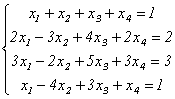
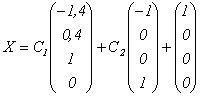
частное решение

Билет №16

Линейный оператор в (В линейном пространстве). Матрица линейного пространства

Линейные операторы. Матрица линейного оператора. Примеры линейных операторов.

Определение. Если каждому элементу 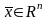ставится в соответствие единственный элемент 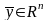, то говорят, что в пространстве Rⁿ задан оператор, действующий в пространстве Rⁿ.

Результат действия оператора A на элемент обозначают .

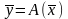Если элементы и связаны соотношением , то называют образом элемента ; элемент — прообразом элемента .

Множество элементов пространства Rⁿ, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A).

Множество элементов пространства Rⁿ, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если , то .

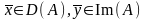Ядром оператора называется множество элементов пространства Rⁿ, образом которых является нуле

нулевой элемент. Ядро оператора обозначают Ker(A): .

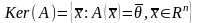Определение. Оператор A, действующий в пространстве Rⁿ называется линейным оператором, если для любых 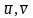из Rⁿ и для любого числа α справедливо:

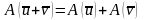и .

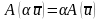Определение. Матрица, столбцами которой являются координаты образов соответствующих базисных векторов некоторого базиса в Rⁿ —

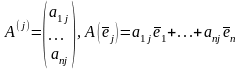
называется матрицей линейного оператора

Билет №17

Действия с линейными операторами и их матрицами

Рассмотрим линейный оператор , действующий в конечномерном линейном пространстве . Доказано, что образ линейного оператора линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается .

Ядром линейного оператора называется множество элементов из , образом которых является нулевой элемент. Ядро оператора обозначают : . Ядро линейного оператора линейное пространство; размерность ядра линейного оператора называется дефектом оператора, обозначается : .

Для линейного оператора, действующего в n-мерном линейном пространстве , справедливы следующие утверждения:

сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор: ;

ранг оператора равен рангу его матрицы;

ядро оператора совпадает с множеством  решений линейной однородной системы с матрицей , размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;

столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.

Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.

Билет №18

Преобразование координат вектора и матрицы линейного оператора. Их свойства и вычисления.

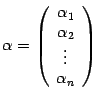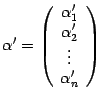Пусть в -мерном линейном пространстве выбран базис , который мы будем для удобства называть "старый" и другой базис , который мы будем называть "новый". Возьмем призвольный вектор из . Его координатный столбец в старом базисе обозначим , а в новом -- . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

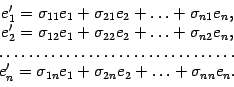
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.