- •Геометрические векторы.
- •Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов.
- •Определители n-го порядка. Вычисление и свойства.
- •Матрица. Линейные операции с матрицами. Умножение матриц, обратная матрица.
- •Элемнтарные преобразования матриц. Приведение к ступенчатому виду.
- •Пространство арифметических векторов (линейное пространство).
- •Линейная зависимость. Базис. Линейное пространство в (линейного пространства)
- •Метрические соотношения в Rn
- •Фундаментальная система решений линейного однородного уравнения
- •Изменение матрицы линейного преобразования при изменении базиса
Метрические соотношения в Rn
Определение.
Если
каждой паре векторов
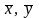 из
пространства Rn
поставлено
в соответствие действительное число
из
пространства Rn
поставлено
в соответствие действительное число
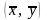 ,
так, что для любых
,
так, что для любых
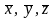 из Rn
и любого действительного числа
из Rn
и любого действительного числа
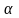 справедливы следующие равенства:
справедливы следующие равенства:
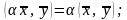
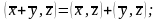
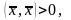 при
при
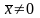 ,
,
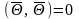 ,
,
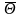 —
нулевой вектор,
—
нулевой вектор,
то говорят, что в пространстве Rn определено скалярное произведение .
Пример. Легко проверить, что изученное в разделе «аналитическая геометрия» скалярное произведение известное из школьного курса скалярное произведение в трехмерном пространстве геометрических векторов (в R3) является скалярным произведением в определенном выше смысле.
Пример. Рассмотрим пространство арифметических векторов R2 ={X=(x1, x2)}. Определим скалярное произведение следующим образом:
(X, Y) = 2x1y1 + 3x2y2.
Легко убедиться, что для определенного таким образом скалярного произведения справедливы аксиомы 1. — 4.:
(X, Y) = 2x1y1 + 3x2y2 = 2y1x1 + 3y2x2 = (Y, X),
(X, Y) = 2(x1)y1 + 3(x2)y2 = (2y1x1 + 3y2x2) = (X, Y),
(X+Y, Z) = 2(x1+y1)z1 + 3(x2+y2)z2 = (2x1z1 + 3x2z2) + (2y1z1 + 3y2z2) = (X, Z) + (Y, Z),
(X,
X)
= 2x1x1
+ 3x2x2
= 2x12
+ 3x22
>0 если
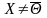 ,
если же X
= (0, 0), то (X,
X)
= 0.
,
если же X
= (0, 0), то (X,
X)
= 0.
Вернемся
к пространству арифметических векторов
Rn
= {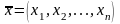 }
}
Определим
в Rn
естественное
скалярное
произведение:
каждой паре векторов
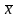 и
и
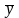 из
этого пространства поставим в соответствие
действительное число
из
этого пространства поставим в соответствие
действительное число
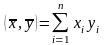 .
Нетрудно доказать, что для любых векторов
,
и
.
Нетрудно доказать, что для любых векторов
,
и
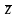 и
любого действительного числа
для
справедливо:
и
любого действительного числа
для
справедливо:
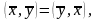
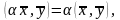
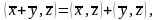
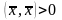 при
при
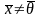 ,
и
,
и
 тогда и только тогда, когда
тогда и только тогда, когда
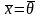 ,
,
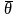 —
нулевой вектор.
—
нулевой вектор.
Пространство арифметических векторов Rn с определенным в нем естественным скалярным произведением называют евклидовым пространством арифметических векторов и иногда обозначают En.
Свойства скалярного произведения. Неравенство Коши-Буняковского
Теорема
(неравенство Коши-Буняковского).
Для любых векторов
из
пространства Rn
справедливо
следующее неравенство
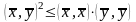 .
.
Доказательство
теоремы. Возьмем
произвольное число
и рассмотрим
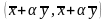 .
По последнему свойству скалярного
произведения для любых векторов
и
любого числа
справедливо:
.
По последнему свойству скалярного
произведения для любых векторов
и
любого числа
справедливо:
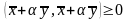 .
С другой стороны,
.
С другой стороны,
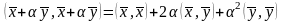 ,
т.е.
,
т.е.
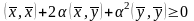 .
Выражение в левой части неравенства —
квадратный трехчлен относительно
.
Он неотрицателен тогда и только тогда,
когда дискриминант
.
Выражение в левой части неравенства —
квадратный трехчлен относительно
.
Он неотрицателен тогда и только тогда,
когда дискриминант
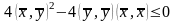 .
Из последнего неравенства немедленно
следует неравенство Коши-Буняковского:
.
Из последнего неравенства немедленно
следует неравенство Коши-Буняковского:
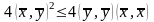 ,
,
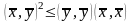 .
Теорема доказана.
.
Теорема доказана.
Метрические соотношения в Rn
Определение.
Число
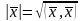 называется длиной вектора
;
число
называется длиной вектора
;
число
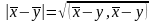 — расстоянием между векторами
и
;
угол
— расстоянием между векторами
и
;
угол
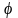 ,
косинус которого
,
косинус которого
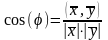 — углом между векторами
и
.
— углом между векторами
и
.
Если
в Rn
скалярное
произведение определено формулой
,
то для любых
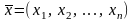 ,
,
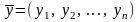 из Rn
справедливо:
из Rn
справедливо:
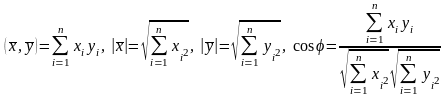
Ортогональность, ортогональные системы, ортонормированные базисы
Определение.
Векторы
и
из
пространства Rn
называются ортогональными, если
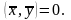
Определение.
Система
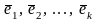 векторов из пространства Rn
называется ортогональной, если векторы
системы попарно ортогональны.
векторов из пространства Rn
называется ортогональной, если векторы
системы попарно ортогональны.
Теорема (о линейной независимости ортогональных систем). Ортогональная система векторов линейно независима.
Доказательство теоремы.
Предположим
противное: векторы
попарно
ортогональны, но они линейно зависимы.
Тогда один из векторов линейно выражается
через остальные. Например, пусть это
первый вектор:
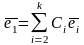 ,
,
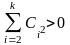 (ясно, что речь идет о ненулевых векторах).
Тогда
(ясно, что речь идет о ненулевых векторах).
Тогда
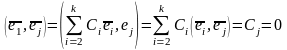 ,
для всех j
= 2,
3, …, k,
т.е.
,
для всех j
= 2,
3, …, k,
т.е.
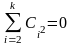 .
Полученное противоречие доказывает
теорему.
.
Полученное противоречие доказывает
теорему.
Определение.
Система
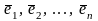 векторов
из пространства Rn
называется
ортонормированной, если векторы системы
попарно ортогональны и имеют единичную
длину.
векторов
из пространства Rn
называется
ортонормированной, если векторы системы
попарно ортогональны и имеют единичную
длину.
Определение. Базис пространства Rn называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину.
В пространстве Rn в естественном скалярном произведении естественный базис — ортонормированный базис.
Билет №11
Система линейных алгебраических уравнений. Матричные уравнения.
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
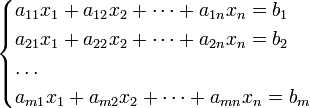
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными.
Составим матрицу А- матрица системы из коэфицентов при неизвестных (матрица)
Тогда исходную систему можно записать как матричное уравнение АХ=В
В том случае если число ур. = числу неизвестных m=n то матрич. Ур-ие АХ=В можно решить домножив обе части равенства на А^-1 слева!
*А*Х= *В
E*X= *В
Х= *В
Если домножим на справа!
Х=В*
А*Х*В=С слева на справа на
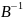
Х= *С *
Если m не равно n то матричное уравнение решают другим способом
Билет №12
Системы n линейных алгебраических уравнений относительно n неизвестных. Правило Крамера.
Правило Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).
Применяется для решения систем линейных уравнений у которых совпадает число неизвестных с числом уравнений.
Если в системе линейных уравнений с неизвестными (дельта не равно 0) , то система имеет решение и притом единственное. Это решение задается формулами
Х=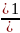 и так же с остальными
и так же с остальными
Определитель
дельта равен
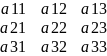
Определитель дельта1 получим из определителя дельта путем замены первого столбца определителя дельта (коэф. Прих1) на столбец свободных членов
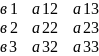
Дельта Х2 получаем из определителя дельта путем замены второго столбца определителя дельта коэф при Х2 на столбец своб членов…..аналогично и для энного
Если дельта равна 0,то два случая
Дельта х1= дельта Х2=0---бесконечно много решений
Одно из них не равно нулю то системарешений не имеет
Билет №13
Свойства решений линейной системы. Нейтральная совместность единой системы. Совместность единой системы.
Если вектор x является решением однородной системы A·x = 0, то вектор αx также является решением этой системы. Здесь α — произвольное число.
Если векторы x и y являются решениями однородной системы A·x = 0, то вектор x + y также является решением этой системы.
Если вектор x является решением однородной системы A·x = 0, а вектор и y — решение неоднородной системы A·x = b, то вектор x + y является решением неоднородной системы A·x = b.
Если векторы x и y являются решениями неоднородной системы A·x = b, то вектор x − y является решением однородной системы A·x = 0.
Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространства Rn. Размерность этого подпространства равна n − r, где r − ранг матрицы системы A.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу матрицы системы.
Это утверждение называют теоремой Кронекера-Капелли.
Система линейных алгебраических уравнений
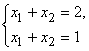
очевидно несовместна.
Ранги расширенной матрицы системы матрицы системы не равны, rank Ap = 2, rankA = 1, rank Ap ≠ rankA:
![]()
Билет №14