25. Абстрактні ряди Фур’є

Є лінійний простір із скалярним добутком

Є поняття норми Відстань Кут

Ортогональність

Означення

1) Система векторів називається ортогональною, якщо

2) Система векторів називається ортонормованою, якщо

3) Система векторів називається лінійно-незалежною, якщо лінійно-незалежна будь-яка скінченна підмножина цієї системи.

Розклад вектора по ортогональній системі векторів називається рядом Фур’є цього вектора.

Приклад

Нехай - множина всіх - періодичних функцій, квадрат яких інтегрований. . - лінійний простір. Скалярний добуток на цій множині .

Для комплекснозначних функцій . Тоді з леми випливає, що система функцій ортогональна відносно введеного скалярного добутку, але не ортонормована.

- ортонормована система. Для - теж ортогональна система на .

- ортонормована

Властивості скалярного добутку

1) Неперервність

Лема

Нехай є скалярний добуток тоді мають місце наступні твердження:

1. Функція - неперервна функція своїх аргументів.

2. Якщо , то .

3. Якщо система векторів ортонормована, і

то .

Доведення

За визначенням, .

1. Нехай . Треба довести, що

Розглянемо

Нерівність Коші – Буняковського

2.

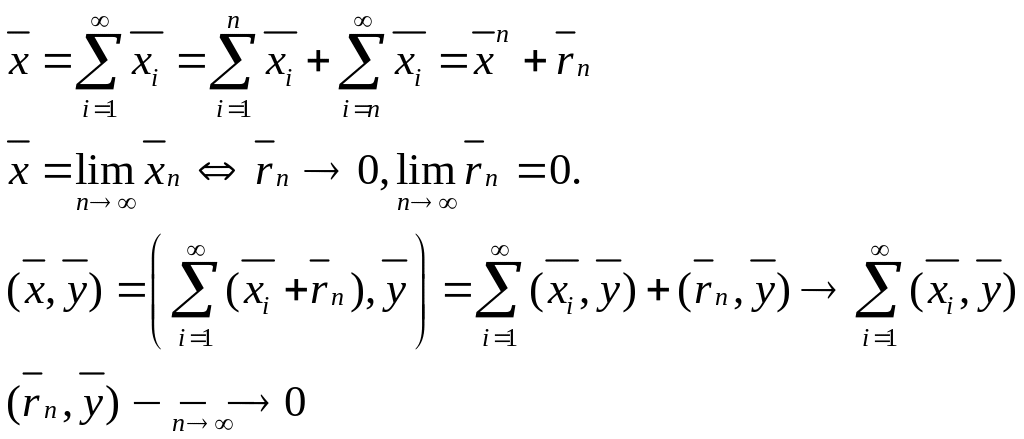
3.

26. Нерівність Коші-Буняковського та теорема Піфагора.

Нехай є скалярний добуток тоді мають місце наступні твердження:

1. Функція - неперервна функція своїх аргументів.

2. Якщо , то .

3. Якщо система векторів ортонормована, і

то .

Доведення

За визначенням, .

1. Нехай . Треба довести, що

Розглянемо

Нерівність Коші – Буняковського

2.

3)Якщо - ортонормована система і , , то =

Спираючись на цю лему, отримаємо теорему Піфагора:

Теорема Піфагора

Якщо - ортогональна система векторів і , то (наприклад, квадрат гіпотенузи рівний сумі квадратів катетів)

Доведення

З пункту 2) леми маємо

Наслідок

Якщо - ортонормована система векторів і , то

(сума квадратів координат).

27. Основні властивості коефіцієнтів Фур’є. Нерівність Бесселя

Нехай - ортонормована система векторів, а - ортогональна система векторів.

З 2) пункту леми

Якщо

Числа називаються коефіцієнтами Фур’є вектора в ортогональній системі (в ортонормованій системі це будуть ).

Означення

Якщо Х - лінійний простір із скалярним добутком, а - ортонормована система ненульових векторів, то кожному вектору в Х відповідає

. Цей ряд і є рядом Фур’є вектора по степеням .

Властивості коефіцієнтів і рядів Фур’є

1. Нехай - скінченна або зліченна система векторів, і нехай вектору відповідає його ряд Фур’є = (ряд збігається до деякого вектора ) . Тоді

ортогональний всій лінійній оболонці системи :   , а також її замиканню.

Доведення

Досить показати, що  .

Наслідок

Оскільки і  , то за теоремою Піфагора

2. Нерівність Бесселя

Оскільки , то .

Ця нерівність,записана через коефіцієнти Фур’є, має назву нерівності Бесселя.

З теореми Піфагора, - це сума ортогональних векторів,

(н-ть Бесселя).

Для ортонормованої системи ця нерівність має вигляд

.

Екстремальні властивості коефіцієнтів Фур’є Якщо ряд Фур’є збігається до :

, то цей вектор дає найкраще наближення вектора серед усіх векторів , що мають вигляд (тобто )

Доведення

Розглянемо

.

(  . За теоремою Піфагора маємо, що це сума квадратів катетів).

Повнота ортогональної системи

Система векторів нормованого простору називається повною по відношенню до множини (система є повна на ), якщо

Справедлива Теорема (умова повноти ортогональної системи)

Нехай - лінійний простір із скалярним добутком і - зліченна або скінченна система ортогональних (попарно ортогональних ) ненульових векторів .

Тоді наступні умови еквівалентні :

1)Система повна в

2) Для має місце розклад в ряд Фур’є

3. Для кожного має місце 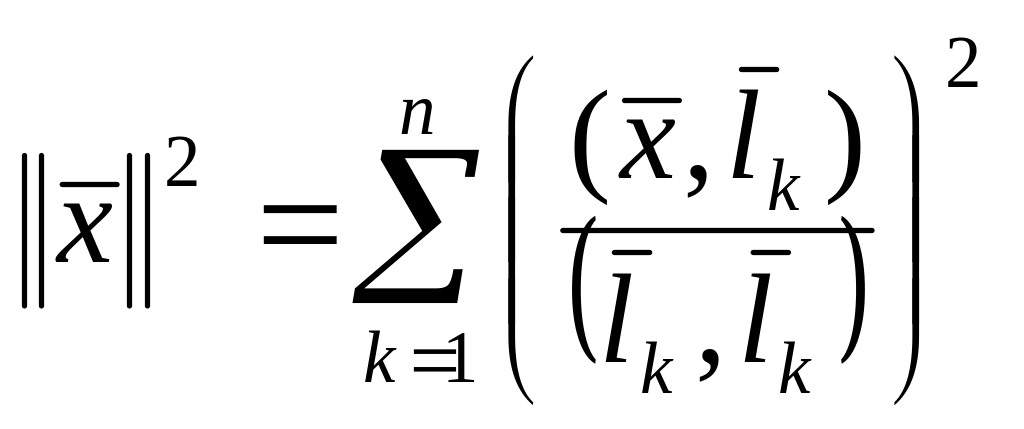- рівність Парсеваля.

1) 2) Це одразу випливає з екстремальних властивостей коефіцієнтів Фур’є .

.

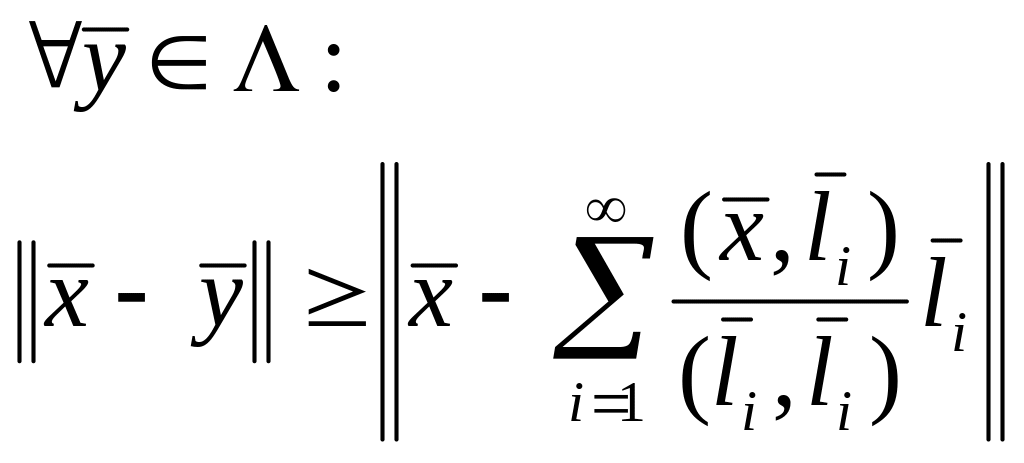
Але з 1) система повна

2) 3) якщо виконується 2) то за теоремою Піфагора маємо 3)

1) 3) Одразу випливає з леми про перпендикулярність ( )

. причому .

Для ортогональної системи

система - повна.

можна розкласти в ряд Фур’є, якщо система повна.