37. Властивоcті перетворень Лапласа

1) Лінійність

Якщо відомі зображення функцій

Приклад

1.

(лінійна комбінація двох функцій).

2) Подібність

Теорема Якщо відоме зображення деякого оригіналу

, то (обмеження вводиться для того, щоб область збіжності інтеграла залишалась такою ж).

Доведення

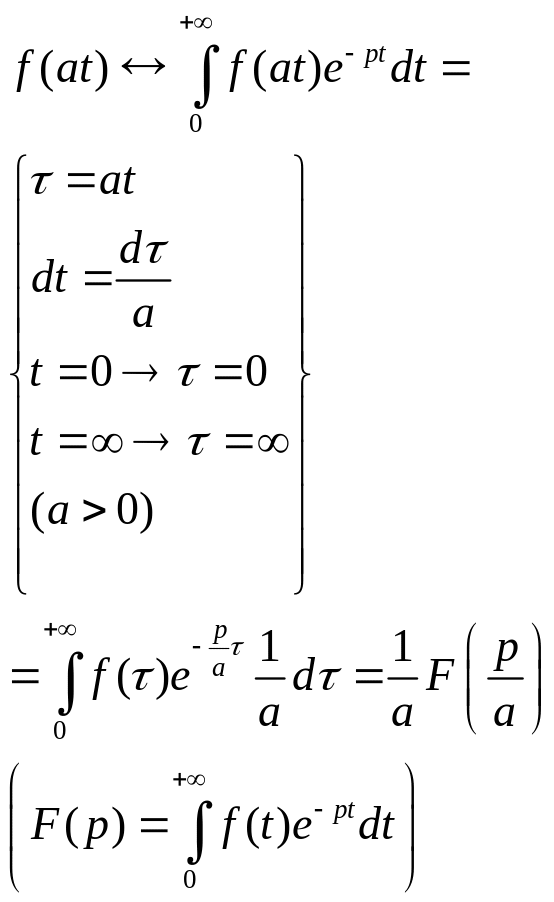
Зауваження Поклавши , отримуємо .

Приклад.

3) Запізнення

Якщо , , то

Доведення

4) Зміщення

Якщо , - число, то

Доведення

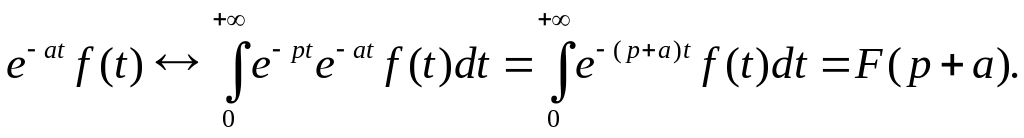
Приклад

38. Диференціювання та інтегрування оригінала та зображення

- оригінал, , і його похідні існують і також є оригіналами, то

(*)

Доведення

Покажемо, що , а це за принципом математичної індукції поширюється на .

Інтегруємо за частинами:

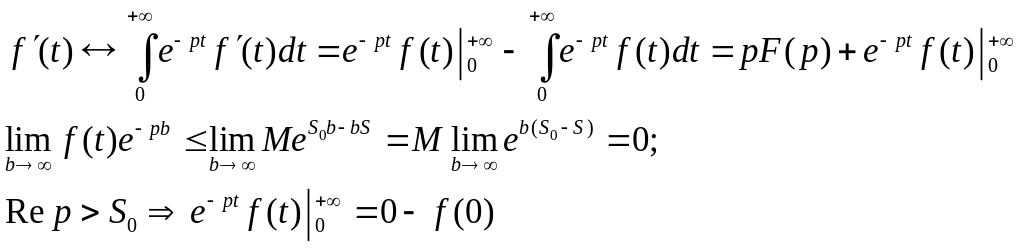
Метод математичної індукції:

1) Для - доведено.

2) Нехай (*) виконується для довільного , тоді для маємо:

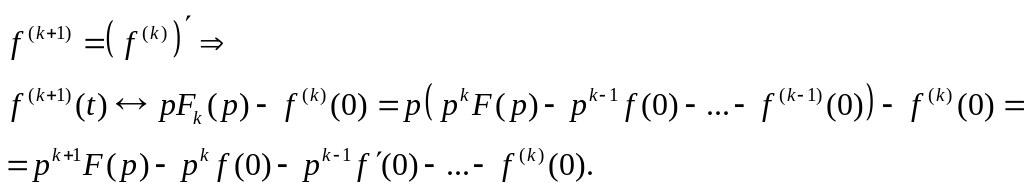
Доведено.

6) Диференціювання зображення

Теорема

Якщо є оригінал , то

Доведення

1) Якщо - оригінал, ,то виконується

Оскільки при - обмежена, тобто . Значить, - теж оригінал . Показником росту є .

2) Оскільки 1) вже доведено, - уже доведено при виводі аналітичної . За методом математичної індукції

7) Інтегрування оригінала

Теорема

Якщо існує оригінал та існує його зображення , то

Доведення

- оригінал, оскільки

.

Умова (2) виконується ,тому (1), (3) теж виконані, отже, - оригінал ,для нього існує перетворення Лапласа.

Нехай . Тоді . Але . Проте , а . Область збіжності .

8) Інтегрування зображення

Теорема

Якщо , і 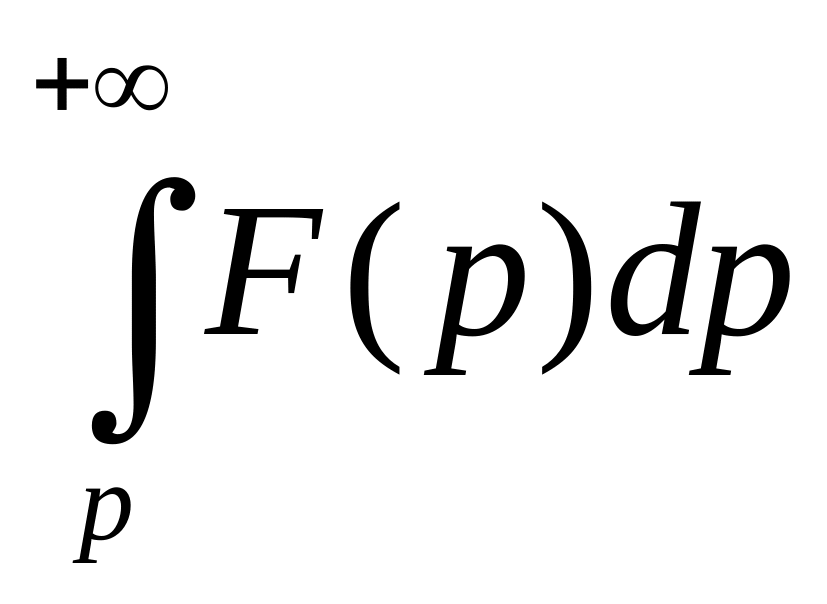збігається (*) в півплощині , то .

Доведення

В півплощині , , інтеграл Лапласа збігається рівномірно по , тому маємо право інтегрувати по :

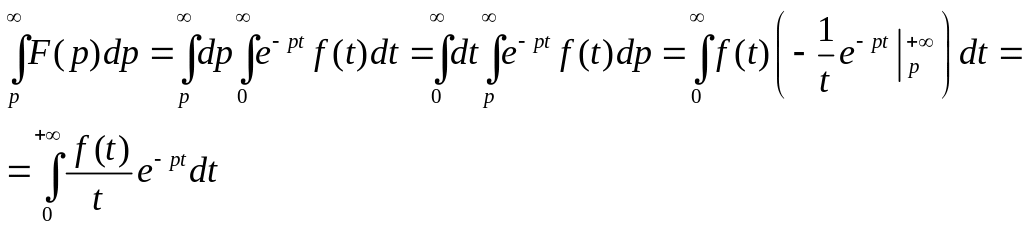
( - будь-яке, але ). Ми показали, що це теж буде оригіналом. Треба перевірити (*). Якщо немає збіжності, це не ьуде оригіналом.

39. Згортка функції. Зображення згортки.

Згорткою неперервних функцій (позначається ) називаєтсья інтеграл .Властивості згортки

1. (доводиться заміною змінних).

2. (і т.д.)

Теорема Бореля

Якщо (оригінал), і , то

, .

Лема Якщо - оригінали, то їх згортка - теж оригінал.

Доведення леми

Нехай

Треба перевірити лише властивість (2) – обмеження на порядок росту.

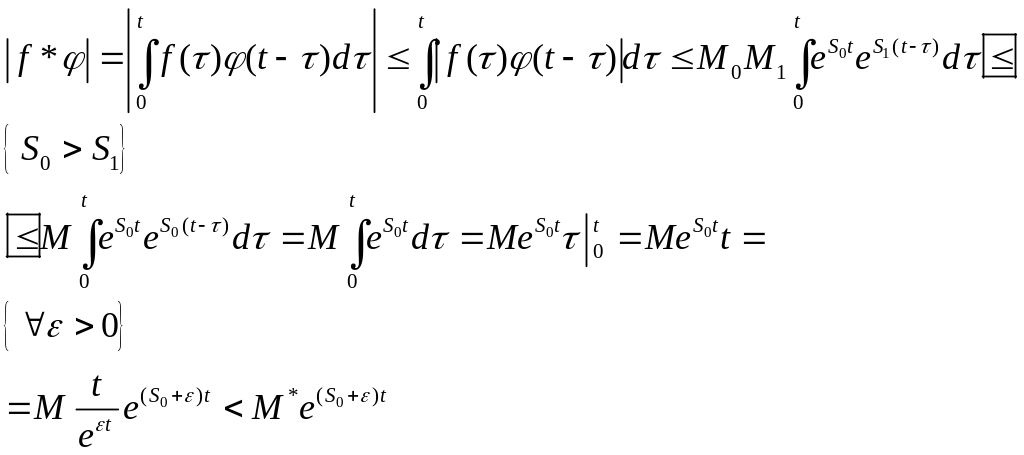
- оригінал.

Доведення теореми

Інтеграл збігається абсолютно, тому

маємо право змінити порядок інтегрування

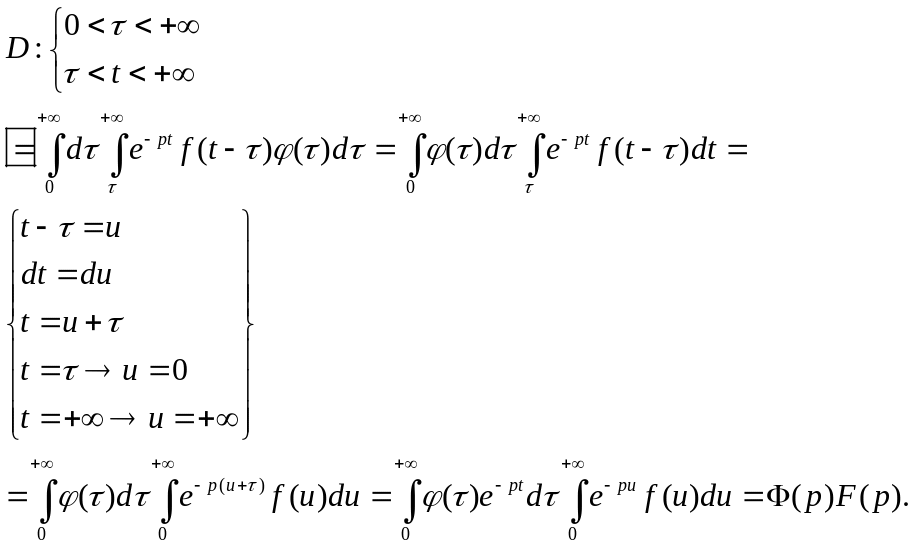
40. Обернене перетворення Лапласа. Формула Рімана-Меліна

Теорема (Рімана - Мелліна)

Нехай є функція , кусково – неперервна, з показником росту , і

абсолютно збігається вздовж прямої . Тоді

Доведення

Функція при абсолютно інтегрована на , оскільки

.

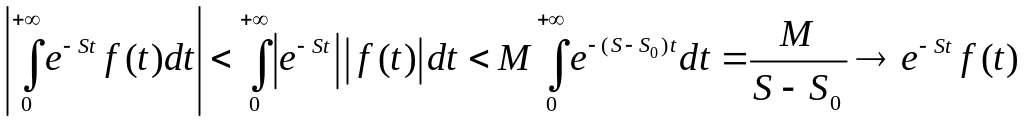Виконані умови представлення її у вигляді інтеграла Фур’є

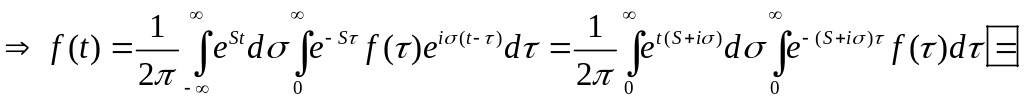
Позначимо міняється вздовж прямої від до :

Доведено.

- формула обернення Рімана – Мелліна.

Теорема розкладу Якщо є зображенням деякого оригіналу, і рівномірно відносно при , то , де - особливі точки функції .

Доведення

Розглянемо контур

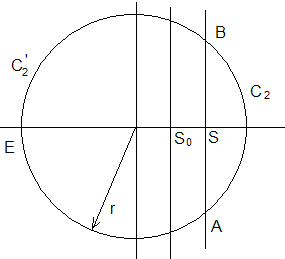
За лемою Жордана другиінтеграл прямує до нуля при .

З іншого боку,

де - особливі точки, що потрапили всередину контура . При туди потрапляють всі особливі точки , бо справа від прямої функція аналітична, особливих точок не має.