
- •Методическое пособие для учащихся вуЗов По дисциплине: физика.
- •Оглавление
- •Колебания и волны Механические колебания Свободные колебания.
- •Гармонические колебания.
- •Незатухающие колебания
- •Частота, период, циклическая частота, амплитуда, фаза колебаний.
- •Смещение, скорость, ускорение колеблющейся системы частиц.
- •Энергия гармонических колебаний.
- •Математический маятник, физический маятник, пружинный маятник.
- •Метод векторных диаграмм. Сложение колебаний одного направления.
- •Биения. Сложение перпендикулярных колебаний. Затухающие механические колебания.
- •Уравнение затухающих колебаний. Амплитуда, частота, коэффициент затухания.
- •Логарифмический декремент затухания, время релаксации, добротность колебательной системы.
- •Вынужденные колебания.
- •Явление механического резонанса.
- •Резонансная частота.
- •Резонанс.
- •Волны в упругой среде.
- •Уравнение плоской бегущей волны.
- •Отличие от уравнения колебаний.
- •Типы волн: продольные и поперечные, плоские, сферические.
- •Волновая поверхность, волновой фронт.
- •Волновое уравнение.
- •Частота, период, длина волны.
- •Свойства волн.
- •Энергия волны.
- •Поток энергии.
- •Вектор Умова.
- •Стоячие волны.
- •Интерференция.
- •Координаты пучностей и узлов стоячей волны.
- •Отличие бегущих волн от стоячих.
- •Электромагнитные волны. Гипотеза Максвелла.
- •Источники электромагнитных волн. Волновое уравнение.
- •Скорость распространения электромагнитных волн.
- •Связь со скоростью света в вакууме.
- •Свойства электромагнитных волн: поперечность, синфазность колебаний векторов напряженностей электрического и магнитного полей.
- •Энергия электромагнитных волн.
- •Вектор Пойнтинга.
- •Шкала электромагнитных волн.
- •Оптика. Геометрическая и волновая оптика.
- •Границы применимости.
- •Принцип Ферма.
- •Полное внутреннее отражение.
- •Интерференция.
- •Оптическая длина пути.
- •Расчет интерференционной картины от двух источников.
- •Координаты минимумов и максимумов интенсивности.
- •Интерференция в тонких пленках.
- •Полосы равной толщины.
- •Кольца Ньютона.
- •Применение интерференции.
- •Просветление оптики.
- •Дифракция.
- •Принцип Гюйгенса-Френеля.
- •Метод зон Френеля.
- •Дифракция Френеля.
- •Пятно Пуассона.
- •Дифракция в параллельных пучках. Дифракционная решетка.
- •Период дифракционной решетки.
- •Поляризация света.
- •Естественный и поляризованный свет.
- •Плоскость поляризации. Степень поляризации.
- •Закон Малюса.
- •Анализаторы и поляризаторы.
- •Закон Брюстера.
- •Двойное лучепреломление.
- •Интерференция поляризованного света.
- •Оптическая ось кристалла.
- •Главное сечение кристалла.
- •Оптически активные вещества.
- •Вращение плоскости поляризации.
- •Электрооптический эффект Керра.
- •Дисперсия света.
- •Нормальная и аномальная дисперсия.
- •Поглощение света веществом.
- •Закон Бугера-Ламберта.
Математический маятник, физический маятник, пружинный маятник.
ФИЗИЧЕСКИЙ МАЯТНИК ФИЗИЧЕСКИЙ МАЯТНИК - см. Маятник.
МАТЕМАТИЧЕСКИЙ МАЯТНИК МАТЕМАТИЧЕСКИЙ МАЯТНИК - см. Маятник.
ОБОРОТНЫЙ МАЯТНИК ОБОРОТНЫЙ МАЯТНИК - физический маятник, который служит для определения ускорения свободного падения g. Имеет две параллельные оси подвеса, расстояние h между которыми изменяют, добиваясь того, чтобы период колебаний Т около каждой из осей имел одинаковую величину. Зная Т и h, определяют g=4p2h/Т2.
МАЯТНИКОВЫЕ ЧАСЫ МАЯТНИКОВЫЕ ЧАСЫ - содержат в качестве регулятора маятник (малые колебания маятника изохронны); изобретены Х. Гюйгенсом (1657). Суточный ход современных наиболее точных маятниковых часов (астрономический) не выше 5.10-4 с.
Метод векторных диаграмм. Сложение колебаний одного направления.
Метод векторных
диаграмм. Каждому гармоническому
колебанию с частотой
![]() можно
поставить в соответствие вращающийся
с угловой скоростью
вектор,
длина которого равна амплитуде
можно
поставить в соответствие вращающийся
с угловой скоростью
вектор,
длина которого равна амплитуде
![]() а
его начальное (стартовое) положение
задается углом
а
его начальное (стартовое) положение
задается углом
![]() совпадающим
с начальной фазой.
совпадающим
с начальной фазой.
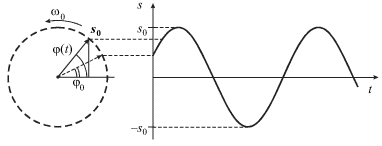
Сложение колебаний одного направления. С помощью векторных диаграмм легко осуществить сложение гармонических колебаний. Так, если необходимо сложить два гармонических колебания с одинаковыми частотами
![]()
то амплитуду
![]() и
начальную фазу
и
начальную фазу
![]() суммарного
колебания
суммарного
колебания
![]() с
той же частотой
можно
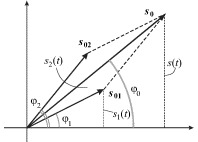
легко рассчитать из рисунка, на котором
графически изображена операция сложения
векторов
с
той же частотой
можно
легко рассчитать из рисунка, на котором
графически изображена операция сложения
векторов
![]() при
при
![]()
![]()
![]()
Биения. Сложение перпендикулярных колебаний. Затухающие механические колебания.
Биения - колебания с периодически меняющейся амплитудой, возникающие в результате наложения двух гармонических колебаний с несклько различными, но близкими частотами. Б. возникают вследствие того, что разность фаз между двумя колебаниями с различными частотами всё время изменяется так, что оба колебания оказываются в какой-то момент времени в фазе, через некоторое время - в противофазе, затем снова в фазе и т.д.
Пусть складывается два колебания с почти одинаковыми частотами, т.е.
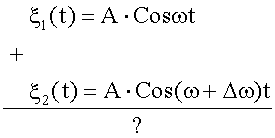 ,
,
![]() .
.
Из тригонометрии: ![]() .
.
Применяя к нашему случаю, получим:
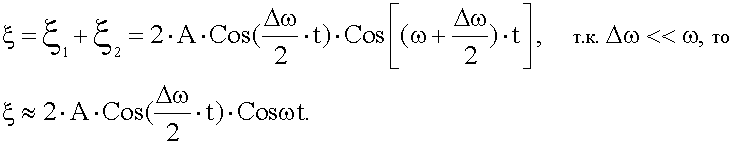
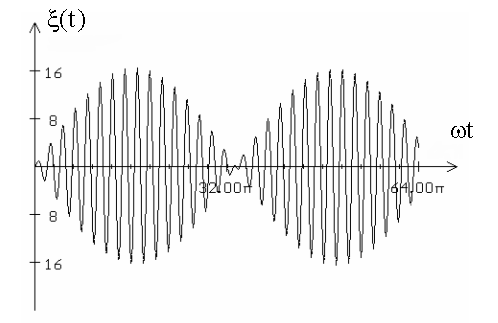
График результирующего колебания - график биений, т.е. почти гармонических колебаний частоты ω, амплитуда которых медленно меняется с частотой Δω .
Амплитуда
![]() из-за
наличия знака модуля (амплитуда всегда
> 0) частота с которой изменяется
амплитуда, равна не Δω / 2 , а в два раза
выше - Δω.
из-за
наличия знака модуля (амплитуда всегда
> 0) частота с которой изменяется
амплитуда, равна не Δω / 2 , а в два раза
выше - Δω.
Сложение
взаимно-перпендикулярных колебаний.
Рассмотрим колебательную систему,
состоящую из точечного груза массы
![]() и
четырех связанных с ним пружин.
и
четырех связанных с ним пружин.
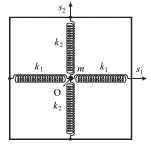
Мгновенное расположение точки m
описывается двумя смещениями из
положения равновесия - точки О:
![]() и
и
![]() Такая
система обладает двумя степенями
свободы. Будем считать смещения малыми.
При таких условиях колебания в двух
взаимно перпендикулярных направлениях
происходят независимо друг от друга:
Такая
система обладает двумя степенями
свободы. Будем считать смещения малыми.
При таких условиях колебания в двух
взаимно перпендикулярных направлениях
происходят независимо друг от друга:
![]()
Здесь собственные частоты гармонических колебаний равны
![]()
Рассмотрим вначале движение груза,
если
![]() (жесткости
всех пружин одинаковы).
(жесткости
всех пружин одинаковы).
![]()
Умножим первое уравнение на
![]() а
второе - на
а
второе - на
![]() и
вычтем второе уравнение из первого. В
результате получим
и
вычтем второе уравнение из первого. В
результате получим
![]()
Теперь умножим первое уравнение на
![]() а
второе - на
а
второе - на
![]() повторим
вычитание и получим
повторим
вычитание и получим
![]()
Наконец, возведем в квадрат каждое из
равенств и сложим их. В результате время
будет исключено, а уравнение траектории
движущегося груза будет уравнением
эллипса:
![]()
Направление движения вдоль траектории
и ориентация эллипса относительно осей
Os1 и Os2 зависят от
начальной разности фаз
![]() На
рис. 1.8 изображены траектории движения
груза при различных значениях
На
рис. 1.8 изображены траектории движения
груза при различных значениях
![]()
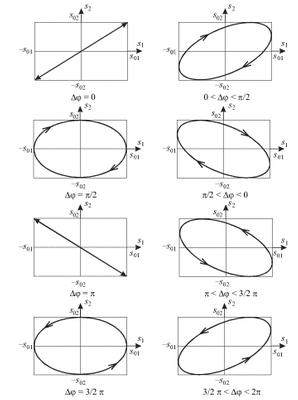
Если частоты двух взаимно-перпендикулярных
колебаний не совпадают, но являются
кратными:
![]() где
и
где
и
![]() -
целые числа, то траектории движения
представляют собой замкнутые кривые,
называемые фигурами Лиссажу (рис. 1.9).
Отметим, что отношение частот колебаний
равно отношению чисел точек касания
фигуры Лиссажу к сторонам прямоугольника,
в который она вписана.
-
целые числа, то траектории движения
представляют собой замкнутые кривые,
называемые фигурами Лиссажу (рис. 1.9).
Отметим, что отношение частот колебаний
равно отношению чисел точек касания
фигуры Лиссажу к сторонам прямоугольника,
в который она вписана.
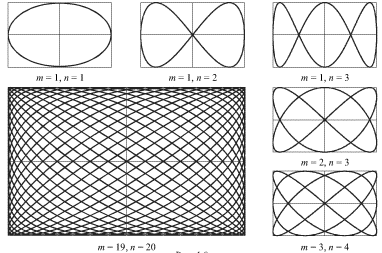
Если кратность между частотами отсутствует, то траектории не являются замкнутыми и постепенно заполняют весь прямоугольник, напоминая нить в клубке.
Затухающие механические колебания. Затухающие колебания – колебания, происходящие в присутствии внешних сил. Амплитуда уменьшается. Сила трения меняется по закону:
![]()
![]()
![]()
![]() -
дифференциальное уравнение затухающих
колебаний
-
дифференциальное уравнение затухающих
колебаний
где,
![]() -коэфициент
затухания.
-коэфициент
затухания.
Амплитуда затухающих колебаний меняется по закону
![]()
Частота не меняется.
