Оптическая длина пути.

ОПТИЧЕСКАЯ ДЛИНА ПУТИ - произведение длины пути светового луча на показатель преломления среды (путь, который прошел бы свет за то же время, распространяясь в вакууме).

Расчет интерференционной картины от двух источников.

Расчет интерференционной картины от двух когерентных источников.

Рассмотрим две когерентные световые волны, исходящие из источников и (рис.1.11.).

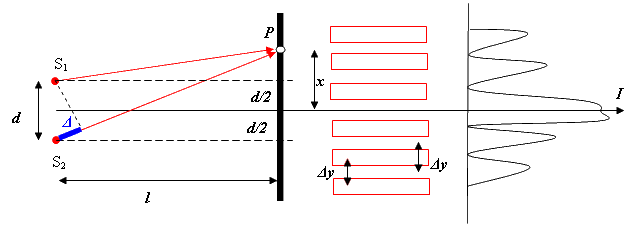
Рис. 1.11.

Экран для наблюдения интерференционной картины (чередование светлых и темных полос) поместим параллельно обеим щелям на одинаковом расстоянии .Обозначим за x - расстояние от центра интерференционной картины до исследуемой точки Р на экране.

Расстояние между источниками и обозначим как d. Источники и расположены симметрично относительно центра интерференционной картины. Из рисунка видно, что

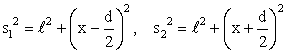
Следовательно

и оптическая разность хода равна

Разность хода составляет несколько длин волн и всегда значительно меньше и , поэтому можем считать, что и . Тогда выражение для оптической разности хода будет иметь следующий вид:

, (1.94)

Так как расстояние от источников до экрана во много раз превосходит расстояние от центра интерференционной картины до точки наблюдения , то можно допустить, что т. е.

, (1.95)

Подставив значение (1.95) в условие (1.92) и выразив х, получим, что максимумы интенсивности будут наблюдаться при значениях

, (1.96)

где - длина волны в среде, а m - порядок интерференции, а х_max -  координаты максимумов интенсивности.

Подставив (1.95) в условие (1.93), получим координаты минимумов интенсивности

, (1.97)

На экране будет видна интерференционная картина, которая имеет вид чередующихся светлых и темных полос. Цвет светлых полос определяется светофильтром, используемым в установке.

Расстояние между соседними минимумами (или максимумами) называется шириной интерференционной полосы. Из (1.96) и (1.97) следует, что эти расстояния имеют одинаковое значение. Чтобы рассчитать ширину интерференционной полосы, нужно из значения координаты одного максимума вычесть координату соседнего максимума

, (1.98)

Для этих целей можно использовать и значения координат двух любых соседних минимумов.

Координаты минимумов и максимумов интенсивности.

Оптическая длина путей лучей. Условия получения интерференционных максимумов и минимумов.

В вакууме скорость света равна , в среде с показателем преломления n скорость света v становится меньше и определяется соотношением (1.52)

Длина волны в вакууме , а в среде - в n раз меньше чем в вакууме (1.54):

При переходе из одной среды в другую частота света не изменяется, так как вторичные электромагнитные волны, излучаемые заряженными частицами в среде, есть результат вынужденных колебаний, совершающихся с частотой падающей волны.

Пусть два точечных когерентных источника света и излучают монохроматический свет (рис.1.11). Для них должны выполнятся условия когерентности: . До точки P первый луч проходит в среде с показателем преломления путь , второй луч проходит в среде с показателем преломления - путь . Расстояния и от источников до наблюдаемой точки называются геометрические длины путей лучей. Произведение показателя преломления среды на геометрическую длину пути называется оптической длиной пути L=ns. L_{1 =} и L_{1 =} - оптические длины первого и второго путей, соответственно.

Пусть и - фазовые скорости волн.

Первый луч возбудит в точке P колебание:

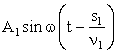, (1.87)

а второй луч - колебание

, (1.88)

Разность фаз колебаний, возбуждаемых лучами в точке P, будет равна:

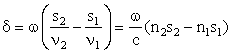, (1.89)

Множитель равен ( - длина волны в вакууме), и выражению для разности фаз можно придать вид

, (1.90)

где

, (1.91)

есть величина, называемая оптической разностью хода. При расчете интерференционных картин следует учитывать именно оптическую разность хода лучей, т. е. показатели преломления сред, в которых лучи распространяются.

Из формулы (1.90) видно, что если оптическая разность хода равна целому числу длин волн в вакууме

, (1.92)

то разность фаз и колебания будут происходить с одинаковой фазой. Число m называется порядком интерференции. Следовательно, условие (1.92) есть условие интерференционного максимума.

Если равна полуцелому числу длин волн в вакууме,

, (1.93)

то , так что колебания в точке P находятся в противофазе. Условие (1.93) - условие интерференционного минимума.

Итак, если на длине равной оптической разности хода лучей , укладывается четное число длин полуволн, то в данной точке экрана наблюдается максимум интенсивности. Если на длине оптической разности хода лучей укладывается нечетное число длин полуволн, то в данной точки экрана наблюдается минимум освещенности.

Напомним, что если два пути лучей оптически эквивалентны, они называются таутохронными. Оптические системы - линзы, зеркала - удовлетворяют условию таутохронизма.