Математическая логика
Логическая операция (логический оператор, логическая связка, пропозициональная связка) — операция над высказываниями, позволяющая составлять новые высказывания путем соединения более простых.
В
качестве основных обычно
называют конъюнкцию (
или
&), дизъюнкцию (
), импликацию (
), отрицание (
).
В смысле классической
логики логические
связки могут быть определены через алгебру
логики.
В асинхронной секвенциальной
логике определена
логико-динамическая связка в виде
операции венъюнкции (
).
Отрицание
Отрица́ние в логике — унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком ¬ перед или чертой над суждением. Синоним: логическое "НЕ".
Как
в классической,
так и в интуиционистской логике
«двойное отрицание» ¬¬A является
следствием суждения A, то есть имеет
место тавтология: 
.
Обратное
утверждение 
верно
в классической логике (закон
двойного отрицания),
но не имеет места в интуиционистской.
То есть, отрицание отрицания искомого
утверждения не может
служить интуиционистским доказательством,
в отличие от классической логики. Это
различие двух логических систем обычно
полагается главным.
Схемотехника
Основная статья: Логические элементы — отрицание
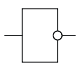
Мнемоническое правило для отрицания звучит так: На выходе будет:
"1" тогда и только тогда, когда на входе «0»,
"0" тогда и только тогда, когда на входе «1»
Конъюнкция
Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И", логи́ческое умноже́ние, иногда просто "И".
Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов. Чаще всего встречаются следующие варианты инфиксной записи:
.
По
аналогии с умножением в алгебре знак
логического умножения может быть
пропущен: 
.
Булева алгебра
В булевой
алгебре конъюнкция
— это функция двух, трёх или более
переменных (они же — операнды операции,
они же — аргументы функции). Переменные
могут принимать значения из множества 
.
Результат также принадлежит множеству
.
Вычисление результата производится по
простому правилу, либо по таблице
истинности.
Вместо значений 
может
использоваться любая другая пара
подходящих символов, например 
или 
или
"ложь", "истина".
Правило:
результат равен
,
если все операнды равны
;
во всех остальных случаях результат
равен
.
Таблицы истинности: для бинарной конъюнкции
для тернарной конъюнкции
-
X
Y
Z
X Y Z
0
0
0
0
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
1
0
1
1
1
1
Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции.