Алгебра логики
Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями[1]. Чаще всего предполагается (т. н. бинарная или двоичная логика, в отличие от, например, троичной логики), что высказывания могут быть только истинными или ложными.
Определение
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B, , , , 0, 1}, где B — непустое множество, над элементами которого определены три операции:
отрицание (унарная операция),
конъюнкция (бинарная),
дизъюнкция (бинарная),
а также константы — логический ноль 0 и логическая единица 1.
Дизъю́нкт — пропозициональная
формула,
являющаяся дизъюнкцией одного
или более литералов (например 
). Конъюнкт — пропозициональная
формула,
являющаяся конъюнкцией одного
или более литералов (например 
).
Аксиомы
Логические операции
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:
B = { Ложь, Истина }
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Опираясь
на этот математический инструментарий, логика
высказываний изучает высказывания и предикаты.
Также вводятся дополнительные операции,
такие как эквивалентность 
(«тогда
и только тогда, когда»),
импликация
(«следовательно»),
сложение по модулю два 
(«исключающее
или»), штрих
Шеффера 
, стрелка
Пирса 
и
другие.
Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция приобретает смысл вычитания из единицы; — немодульного сложения; & — умножения; — равенства; — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR); — непревосходства суммы над 1 (то есть A B = (A + B) <= 1).
Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.
Свойства логических операций
Коммутативность: x
y
= y
x,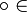 
{&, 
}.Идемпотентность: x x = x, {&, }.
Ассоциативность: (x y) z = x (y z), {&,
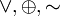}.Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
,
,
.
Законы де Мо́ргана:
,
.
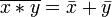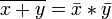Законы поглощения:
,
.
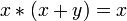Другие (1):
.
.
.
..
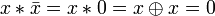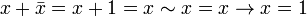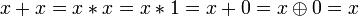Другие (2):
.
.
.
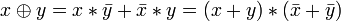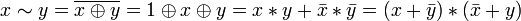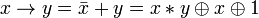Другие (3) (Дополнение законов де Мо́ргана):
.
.
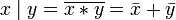Существуют методы упрощения логической функции: например, Карта Карно, метод Куайна - Мак-Класки