Квантор
Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего упоминают:
Квантор всеобщности (обозначение:
,
читается: «для всех…», «для каждого…»
или «каждый…», «любой…», «для любого…»).Квантор существования (обозначение:
,
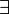читается: «существует…» или «найдётся…»).
В математической логике приписывание квантора к формуле называется связыванием или квантификацией.
В многозначных логиках также вводятся и другие кванторы, например, квантор плюральности (квантор Решера) (обозначается перевёрнутой M, читается означает «для большинства …»).
Примеры
Обозначим P(x) предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные):
любое натуральное число кратно 5;
каждое натуральное число кратно 5;
все натуральные числа кратны 5;
следующим образом:
.
Следующие (уже истинные) высказывания используют квантор существования:
существуют натуральные числа, кратные 5;
найдётся натуральное число, кратное 5;
хотя бы одно натуральное число кратно 5.
Их формальная запись:
.
Введение в понятие
Пусть на множестве Х простых чисел задан предикат Р(х): «Простое число х — нечётно». Подставим перед этим предикатом слово «любое». Получим ложное высказывание «любое простое число х нечётно» (это высказывание ложно, так как 2 — простое чётное число).
Подставив перед данным предикатом Р(х) слово «существует», получим истинное выказывание «Существует простое число х, являющееся нечётным» (например, х=3).
Таким образом, превратить предикат в высказывание можно, поставив перед предикатом слова: «все», «существует», и др., называемые в логике кванторами.
Кванторы в математической логике
Высказывание
означает,
что область значений переменной x включена
в область истинности предиката P(x).
(«При всех значениях (x) утверждение верно»).
Высказывание
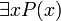означает,
что область истинности предиката P(x) непуста.
(«Существует (x) при котором утверждение верно»).
Вложенные кванторы Свободные и связанные переменные
Множество свободных переменных* формулы F определяется рекурсивно, следующим образом:
Свободные переменные.
Все переменные, входящие в атомарную формулу, являются свободными переменными этой формулы,
свободные переменные формулы F являются свободными переменными формулы ¬F,
переменные, являющиеся свободными для хотя бы одной из формул F или G, являются свободными переменными формулы (F Д G),
все свободные переменные формулы F кроме v являются свободными переменными формулы Kv F.
Замкнутая формула.
Формула без свободных переменных называется замкнутой формулой, или предложением.
Связанная переменная.
Переменная v связана в формуле F, если F содержит вхождение Kv, где K — квантор.
Связанное переименование, свободное переименование
Операции над кванторами
Правило отрицания кванторов — применяется для построения отрицаний высказываний, содержащих кванторы, и имеет вид:
Ограниченные кванторы История появления
Философы давно обращали внимание на логические операции, ограничивающие область истинности предиката, однако не выделяли их в отдельный класс операций. Так, Томас Гоббс считал, что они являются частями имен.
Хотя кванторно-логические конструкции широко используются как в научной, так и в обыденной речи, их формализация произошла только в 1879 г., в книге Фреге «Исчисление понятий». Обозначения Фреге имели вид громоздких графических конструкций и не были приняты. Впоследствии было предложено множество более удачных символов, но общепринятыми стали обозначения для квантора существования, предложенное Чарльзом Пирсом в 1885 г., и для квантора общности, образованное Герхардом Генценом в 1935 г. по аналогии с символом квантора существования (перевёрнутые первые буквы англ. exists, all — существует, все). Термины «квантор», «квантификация» также предложил Пирс.
20