Элементарная дизъюнкция

В логике высказываний элементарной дизъюнкцией называется дизъюнкция литералов:

, где l_i — литералы.

В англоязычной литературе для обозначения элементарной дизъюнкции используется термин клоз (англ. clause).

Элементарная конъюнкция

В логике высказываний элементарной конъюнкцией называется конъюнкция литералов:

, где l_i — литералы.

14

Исчисление высказываний.

Давая описание алгебры высказываний, мы пользовались логическими значениями высказываний (истина, ложь). Но понятия истинности и ложности не математические. Эти понятия во многих случаях субъективны и, скорее, относятся к философии.

В связи с этим желательно построить математическую логику, не пользуясь понятиями истинности и ложности. Необходимо также при этом построении не применять самих законов логики.

§ 1. Понятие формулы исчисления высказываний.

Исчисление высказываний – это аксиоматическая логическая система, интерпретацией которой является алгебра высказываний.

Описание всякого исчисления включает в себя описание символов этого исчисления (алфавита), формул, являющихся конечными конфигурациями символов, и определение выводимых формул.

Алфавит исчисления высказываний состоит из символов трех категорий:

1. Символы первой категории: 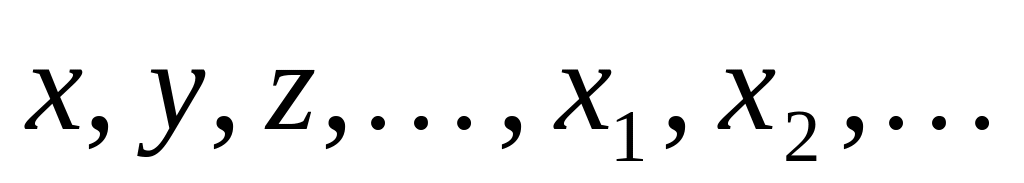Эти символы будем называть переменными высказываниями.

2. Символы второй категории: 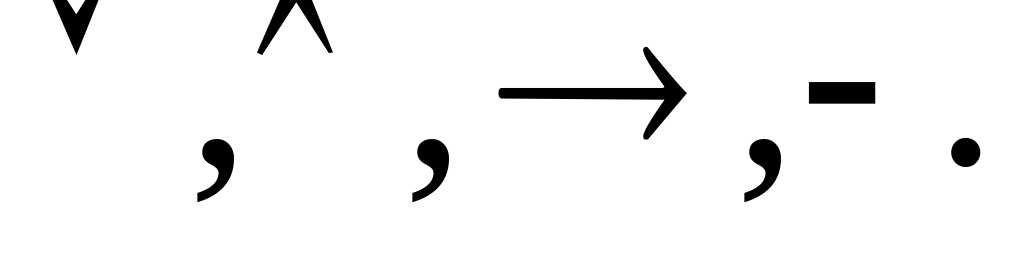они носят общее название логических связок. Первый из них – знак дизъюнкции или логического сложения, второй – знак конъюнкции или логического умножения, третий – знак импликации или логического следования и четвертый – знак отрицания.

3. Третью категорию составляет пара символов ( ), называемая скобками.

Других символов исчисление высказываний не имеет.

Формулы исчисления высказываний представляют собой последовательности символов алфавита исчисления высказываний. Для обозначения формул будем пользоваться большими буквами латинского алфавита. Эти буквы не являются символами исчисления. Они представляют собой только условные обозначения формул.

Определение формулы исчисления высказываний.

1. Всякая переменная является формулой.

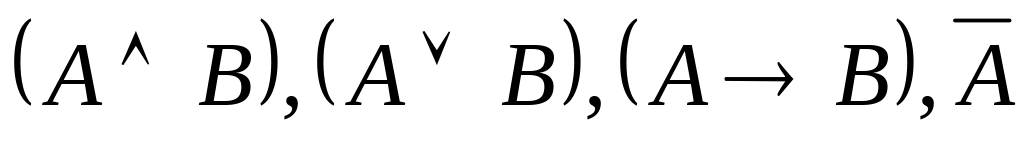2. Если А и В- формулы , то слова - тоже формулы.

3. Никакая другая строчка символов не является формулой.

Переменные высказывания будем называть элементарными формулами.

Приведем примеры формул исчисления высказываний.

Переменные высказывания являются формулами согласно п.1 определения формулы. Но тогда слова являются формулами согласно п.2 определения. По этой же причине будут формулами слова:

Очевидно, не являются формулами слова: поскольку одни из них не взяты в скобки, в других скобка лишь одна,…

Одновременно с понятием формулы вводится понятие подформулы или части формулы.

1. Подформулой элементарной формулы является она сама.

2. Если формула имеет вид , то ее подформулами являются: она сама, формула А и все подформулы формулы А.

3. Если формула имеет вид (А*В)(здесь и в дальнейшем под символом * будем понимать любой из трех символов 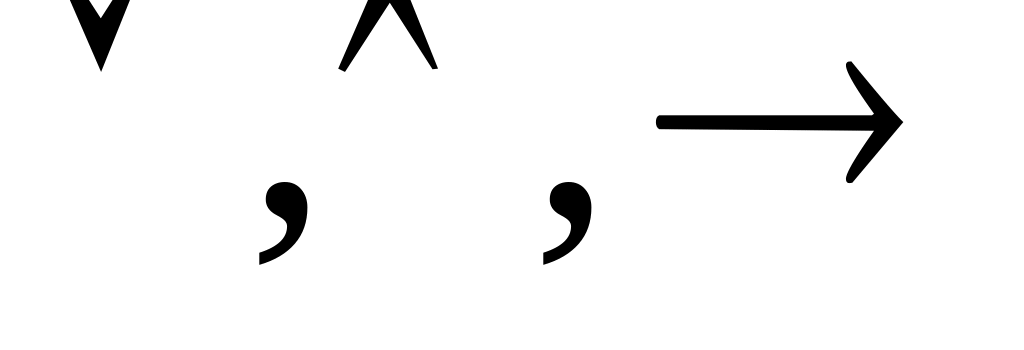), то ее подформулами являются: она сама, формулы А и В и все подформулы формул А и В.

Например, для формулы ее подформулами будут:

- подформула нулевой глубины,

-подформулы первой глубины,

-подформулы второй глубины,

-подформулы третьей глубины,

-подформула четвертой глубины.

Таким образом, по мере “погружения вглубь структуры формулы” мы выделяем подформулы все большей глубины.

Очевидно, что на самой большой глубине находятся лишь элементарные формулы. Однако элементарные формулы могут быть и на других глубинах.

Введем в запись формул некоторые упрощения. Будем опускать в записи формул скобки по тем же правилам, что и в алгебре высказываний.

В связи с этими правилами формулы будем писать соответственно.

15