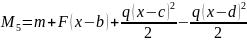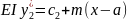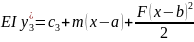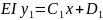- •1)Задачи тмм. Понятие термина «машина». Классификация машин.
- •2)Понятие термина «механизм». Основные виды механизмов.
- •3)Звенья механизма. Кинематические пары. Классификация кинематических пар.
- •4)Кинематические цепи. Группы Ассура.
- •5)Структурный анализ механизмов
- •6) Принцип образования рычажных механизмов.
- •7)Основные виды рычажных механизмов.
- •8)Задачи кинематического анализа механизмов. Определение положений звеньев, перемещений и траекторий точек звеньев.
- •15) Определение реакций в кинематических парах рычажных механизмов
- •10)Определение скоростей звеньев и точек звеньев графоаналитическими методами (метод планов скоростей).
- •11)Определение ускорений звеньев и точек звеньев графоаналитическими методами (метод планов ускорений).
- •12) Кинематический анализ механизмов аналитическими методами.
- •13) Силы, действующие в механизмах.
- •14) Задачи силового анализа механизмов. Принцип Даламбера.
- •9) Определение скоростей звеньев и точек звеньев численными методами
- •16) Определение приведенных моментов (сил) и приведенных масс (моментов инерции) динамической модели
- •17) Основные виды зубчатых механизмов
- •18) Кинематика зубчатых механизмов с неподвижными осями.
- •19) Кинематика зубчатых механизмов с подвижными осями.
- •20) Основная теорема зубчатого зацепления.
- •21) Основные геометрические параметры зубчатого колеса.
- •22) Задачи и методы сопротивления материалов.
- •23) Допущения и модели прочностной надежности.
- •24) Внутренние и внешние силы. Главный вектор и главный момент внутренних сил. Метод сечений.
- •25) Напряжения.
- •26) Перемещения и деформации.
- •27) Закон Гука и принцип независимости действия сил.
- •28)Внутренние силы и напряжения при растяжении-сжатии.
- •29) Закон Гука при растяжении-сжатии.
- •30) Построение эпюр продольных сил, нормальных напряжений и перемещений.
- •31) Статически определимые и статически неопределимые системы при растяжении-сжатии.
- •32) Потенциальная энергия деформации.
- •33) Испытание материала на растяжение-сжатие. Диаграмма растяжения.
- •34) Напряжения в наклонных сечениях при растяжении-сжатии.
- •35) Закон парности касательных напряжений.
- •43)Построение эпюр крутящих моментов, касательных напряжений и перемещений.
- •44) Изгиб. Опоры и опорные реакции.
- •4 5) Дифференциальное уравнение упругой линии балки при изгибе.
- •46) Построение эпюр поперечных сил и изгибающих моментов.
- •47) Построение эпюр перемещений при изгибе аналитическими методами.
- •52) Понятие об устойчивости стержней. Задача Эйлера.
- •53) Пределы применимости формулы Эйлера.
- •54) Практические методы расчета продольно сжатых стержней.
- •5 5) Статические моменты сечения.
- •5 6) Моменты инерции сечения.
- •57) Главные оси и главные моменты инерции.
- •58) Вычисление моментов инерции сложных сечений.
- •59) Переменные напряжения. Циклы переменных напряжений.
- •60) Кривая усталости и диаграмма предельных амплитуд напряжений.
- •61) Основные факторы, влияющие на предел выносливости.
- •62) Расчеты на прочность конструкций при переменных напряжениях.
- •63) Теории прочности.
- •64) Расчеты на прочность конструкций при динамических нагрузках.
- •65) Определение перемещений и напряжений при ударе.
43)Построение эпюр крутящих моментов, касательных напряжений и перемещений.
Наглядное представление о законе изменения крутящих моментов по длине стержня дает эпюра крутящих моментов, ось абсцисс которой проводится параллельно оси стержня, а ось ординат ей перпендикулярно. По оси ординат в выбранном масштабе откладываются значения крутящих моментов в поперечных сечениях стержня.
Для наглядного
изображения изменения касательных
напряжений в поперечных сечениях
стержня по его длине строиться эпюра
касательных напряжений. Эпюру касательных
напряжений получим, разделив значения
Мк на соответствующие полярные
моменты кручения стержня, использую
формулу

Эпюра перемещений
–график, изображающий изменение. Для
построение эпюры перемещений определяем
перемещения характерных сечений по
формуле

44) Изгиб. Опоры и опорные реакции.
Изгиб–такой вид деформации, когда под действием внешних сил в поперечных сечениях стержня возникают изгибающие моменты.
В ыбираем
систему координат. Освобождаемся от
опор и, так как направление этих реакций
неизвестно, принимаем их направление
в положительном направлении оси y.
ыбираем
систему координат. Освобождаемся от
опор и, так как направление этих реакций
неизвестно, принимаем их направление
в положительном направлении оси y.

Для определения реакций двухопорной балки используем уравнения равновесия:



Для определения реакций консольно закрепленной балки используем уравнения равновесия:
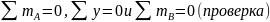
Подписываем значения реакций на расчетной схеме.
4 5) Дифференциальное уравнение упругой линии балки при изгибе.
Интегрируем
Находим сi : при х=0 с=EIy0/=EIφ0 . При х=а с1=с2 и т.д. Тогда с1=с2=…=EIφ0
Второе интегрирование
Получаем D1=D2=…=D5=EIy0

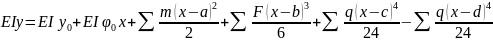
46) Построение эпюр поперечных сил и изгибающих моментов.
Эпюра поперечных сил или изгибающих моментов есть график, ординаты которого в каждой точке выражают в масштабе величину поперечной силы или изгибающего момента. Положительные значения поперечной силы или изгибающего момента откладываются вверх от оси, отрицательные – вниз.
Графическое изображение изменения поперечных сил и изгибающих моментов по длине балки весьма удобно, так как придает расчету наглядность, позволяет быстро определять опасные сечения и соответственно облегчает требуемый расчет балки.
Построение эпюр рекомендуется проводить в следующей последовательности.
1. Рассматриваем исходную схему балки и выполняем расчетную схему. Расчетная схема – это схема, выполненная с учетом исходных данных примерно в масштабе.
2. Освобождаем балку от связей, заменяя действие связей силами реакций, выбрав при этом систему осей декартовых координат. Напомним, что определение реакций связей имеет свой алгоритм решения, который был подробно рассмотрен ранее.
3. Разбиваем схему балки на силовые участки. Границами силовых участков являются: сечения приложения сосредоточенных сил и моментов сил; сечения изменения профиля балки; граничные сечения приложения распределенных нагрузок – q (сечения начала и конца действия ); концевые сечения балки.
4. На каждом силовом участке определяем закон изменения соответствующего внутреннего силового фактора (поперечной силы или изгибающего момента) по длине участка балки.
5. Проведя нулевую линию, строим соответствующую эпюру.
6. Анализируя полученные эпюры, выявляем опасные сечения и проводим необходимые расчеты.