Использование трехмерных моделей для расчета изделий методами имитационного моделирования

Имитационное моделирование заключается в создании модели проектируемого объекта и экспериментирования с ней при реальных условиях и ограничениях.

Имитация в САПР осуществляется путем создания модели проектируемого объекта и наблюдения за его функционированием до реального его изготовления с целью нахождения его рациональных параметров. Различают кинематическую и динамическую имитацию.

Кинематическая имитация осуществляется с целью проверки работоспособности объекта в процессе движения его элементов (проверка коллизий, например, столкновений). Примеры: контрольные сборки, работа движущегося механизма.

Динамическая имитация осуществляется путем исследования поведения объекта при изменении действующих на него нагрузок и температур. Определяются теплонапряженное состояние и деформации элементов объекта. Применение при таких расчетах аналитических моделей, полученных методами математической физики, применительно к сложным по конфигурации объектам, в настоящее время невозможно, так как при этом необходимо принимать ограничения, которые зачастую нарушают адекватность математической модели объекта. Поэтому для решения задач динамической имитации в САПР используют приближенные методы: метод конечных элементов (МКЭ) и метод конечных разностей (МКР). Как показала практика, МКЭ является самым эффективным методом решения задач имитационного моделирования в САПР. В основе этого метода лежит представление объекта исследования в виде набора некоторых простых с геометрической точки зрения фигур, называемых конечными элементами, взаимодействующими между собой только в узлах. Расположенные определенным образом (в зависимости от конструкции объекта) и закрепленные в соответствии с граничными условиями конечные элементы, форма которых определяется особенностями моделируемого объекта, позволяют описать все многообразие механических конструкций и деталей.

При выполнении инженерных расчетов на прочность неизбежен этап создания моде­лей прочностной надежности элементов конструкций. С помощью таких моделей возмож­но выбрать материал и необходимые размеры конструкций и оценить ее сопротивление внешним воздействиям.

Надежностью называют свойство изделия выполнять свои функции в заданных пре­делах в течение требуемого промежутка времени. Прочностной надежностью называют отсутствие отказов, связанных с разрушением или с недопустимыми деформациями, или, вообще, с наступлением предельного состояния в определенном смысле. Основной мерой надежности является вероятность безотказной работы изделия.

Другой, более распространенной величиной оценки прочностной надежности являет­ся запас прочности. Пусть р — параметр работоспособности изделия (например, дейст­вующее усилие, давление, эквивалентное напряжение в опасной точке и т. п.). Тогда запа­сом прочности называют отношение

n =

где Ркр—критическое (предельное) значение параметра Р , нарушающее нормальную работу изделия, Рмах — наибольшее значение параметра в рабочих условиях. Условие прочностной надежности записывается в виде:

n [n],

где [n] — допустимое значение запаса прочности. Допустимый запас прочности назна­чают на основании инженерного опыта эксплуатации подобных конструкций (прототи­пов). Ряд отраслей техники имеют нормы прочности, в которых допустимые запасы проч­ности регламентированы для разных условий эксплуатации. Обычный диапазон изме­нений [n] колеблется от 1, 3 (при стабильных условиях нагружения) до 5 и более (при пе­ременных и динамических нагрузках). В практике расчетов используют как аналитические, так и численные методы. Первые базируются на математических методах решения краевых задач, обычно сложных и тру­доемких, и зачастую ограничены достаточно простыми геометрическими формами тел и схем нагружения. Численные методы, к которым относятся, в частности, метод конечных разностей, метод граничных интегральных уравнений, метод граничных элементов, метод конечных элементов и другие методы, напротив, не ограничены ни формой тел, ни спосо­бом приложения нагрузки. Это, наряду с повсеместным распространением мощной вы­числительной техники, способствует их распространению в инженерной среде.

Основная идея метода конечных элементов состоит в том, что любую непрерывную величину (перемещение, температура, давление и т. п.) можно аппроксимировать моделью, состоящей из отдельных элементов (участков).

Объект представляется в виде набора простых (с геометрической точки зрения) фигур, называемых конечными элементами (для плоской задачи-прямоугольники, треугольники, для объемной задачи-параллепипеды, призмы, тетраэдры), которые взаимодействуют между собой в узлах. Элементы могут быть линейными и параболическими (имеющие узлы в серединах ребер). На каждом из этих элементов исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, которая строится на значениях исследуемой непрерывной величины в конечном числе точек рассматриваемого элемента. Для этого используются линейная (первого порядка) или параболическая (второго порядка) функции.

К узлам прикладываются граничные условия: кинематические (закрепления, перемещения) и статические (нагрузки), в результате чего тело деформируется. Условие равновесия каждого элемента:

Р=[Kэ]U,

где Р-вектор усилий, U-вектор перемещений, [Kэ]-матрица жесткости конечного элемента, в которую входят модуль упругости (Юнга) E, характеризующий сопротивление материала упругой деформации (отношение напряжения к вызванной им упругой деформации) и коэффициент Пуассона μ (отношение поперечной деформации к продольной).

Матрицы жесткости всех конечных элементов объединяются в глобальную матрицу жесткости [K], перемещения и усилия в узлах объединяются соответственно в общие столбцы перемещений [U] и усилий [P].

В результате создается система линейных уравнений, в которой неизвестными являются перемещения:

[U] = [K] [P]

Решается система уравнений с вычислением перемещений каждого узла. Это стало возможным, когда в 1963 г. было доказано, что этот МКЭ можно рассматривать как один из вариантов известного в строительной механике метода Рэлея—Ритца, который путем минимизации потенциаль­ной энергии позволяет свести задачу к системе линейных уравнений равновесия. То есть полученное решение соответствует минимуму потенциальной энергии деформированной упругой системы.

Перемещения связаны с соответствующими напряжениями законом Гука:

σ=[E] ε

Для визуальной оценки полученных результатов расчета распределение значений полученных параметров (напряжений, деформаций) представляется в виде изолиний (на которых значение параметра постоянно), цвет и насыщенность которых изменяется в зависимости величины параметра. Кроме того, для визуальной качественной оценки деформированного состояния объекта, деформации показываются искаженно.

Например, плоскую ферменную конструкцию можно смоделировать набором плоских стержневых фигур, рамную - набором объемных стержневых элементов, различного рода пластины и оболочки - множеством плоских треугольников или прямоугольников. Геометрически объемные тела удобно представлять в виде совокупности элементарных пирамид, параллелепипедов и призм.

Такое представление рассматриваемого объекта позволяет решать задачи расчета напряженного и деформированного состояний тела, устойчивости и динамики, нахождения частот и амплитуд собственных и вынужденных колебаний.

Программное обеспечение для решения задач методом МКЭ должно включать в себя следующие элементы: редактор разбивки на конечные элементы, ядро, непосредственно обеспечивающее решение, и визуализатор для демонстрации полученных результатов.

Рассмотрим физические основы этого метода на примере решения плоской задачи теории упругости - расчета напряженного состояния тонкой пластины произвольной формы. В качестве конечного элемента примем плоский элемент треугольной геометрической формы.

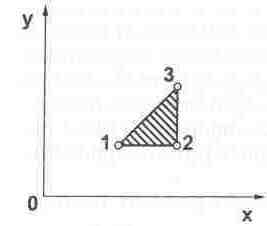
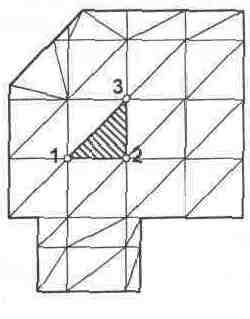
Рассмотрим конечный элемент, координаты узлов

которого равны и . После приложения внешней нагрузки тело деформируется, и каждая внутренняя точка этого элемента с координатами х,у занимает новое положение, перемещаясь в направлении координатных осей х и у соответственно на расстояния u(х,у) и v(x,y), причем в пределах одного конечного элемента эти перемещения представляются в виде линейных функций координат:

, (1)

или, в матричной форме,

, (2)

где ; ;

.

Необходимо отметить, что задание перемещений в виде линейных функций (1) обеспечивает сшивку этих функций на границах соседних элементов, так как линейность перемещений в узлах означает и их линейность везде вдоль границы элемента.Подставляя в (2) координаты узловых точек, получаем:

,

или

, (3)

где .

В системе уравнений (3) в качестве неизвестных можно рассматривать постоянные коэффициенты . Разрешая (3) относительно с помощью формул Крамера, имеем:

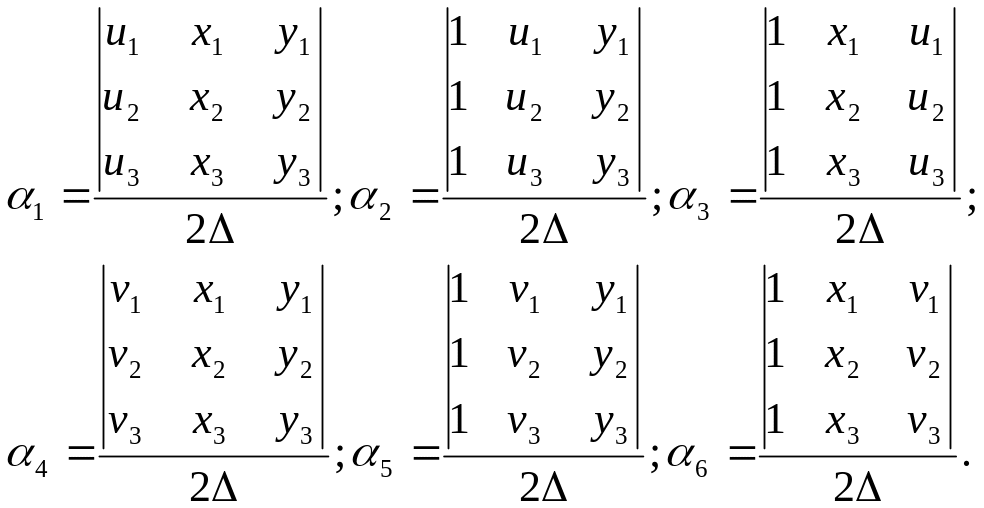(4)

Здесь - определитель матрицы системы, численно равный площади конечного элемента:

Заметим, что тот же самый результат (4) получается и другим способом: поскольку определитель матрицы отличен от нуля, то единственное решение системы (3) есть произведение обращенной матрицы системы и вектора Подстановка (4) в (3) приводит к выражению для определения поля перемещений произвольной точки данного конечного элемента:

(5)

где а остальные коэффициенты находятся путем циклической перестановки индексов 2 и 3. В матричной форме (5) переписывается как:

(6)

Функция , имеющая вид:

(7)

называется функцией формы.

Компоненты вектора - столбца относительной деформации связаны с перемещениями соотношениями:

С другой стороны, используя (6) и (7), можно написать

(8)

где - вектор узловых перемещений,

;

Перемещения связаны с соответствующими напряжениями законом Гука, который для случая плоского нагружения записывается в виде:

, (9)

где

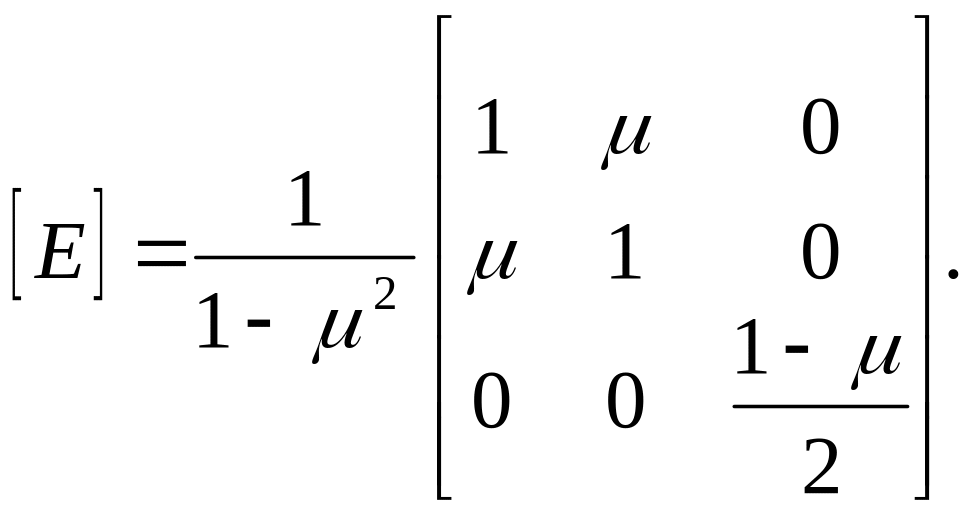
Уравнение (9) с учетом (6) принимает следующий вид:

(10)

Воспользуемся выражением для потенциальной энергии деформации элементарного объема (13). Тогда эта энергия, с учетом (10), определится из очевидного уравнения:

. (11)

Выражение для объема в уравнении (11) представляет собой, в случае плоской задачи, произведение площади конечного элемента на его толщину.

Энергия деформации элемента объема может быть рассчитана иначе - как работа внешних сил. В качестве внешней нагрузки на элемент объема можно принять реакции приложенные к граням этого элемента, тогда:

(12)

Из уравнения (12) легко определить реакции, выполнив ряд очевидных сокращений, тогда

(13)

где

. (14)

Уравнение (13) представляет собой обычное уравнение равновесия, а матрица является квадратной размерности 6х6. Она называется матрицей жесткости конечного элемента,

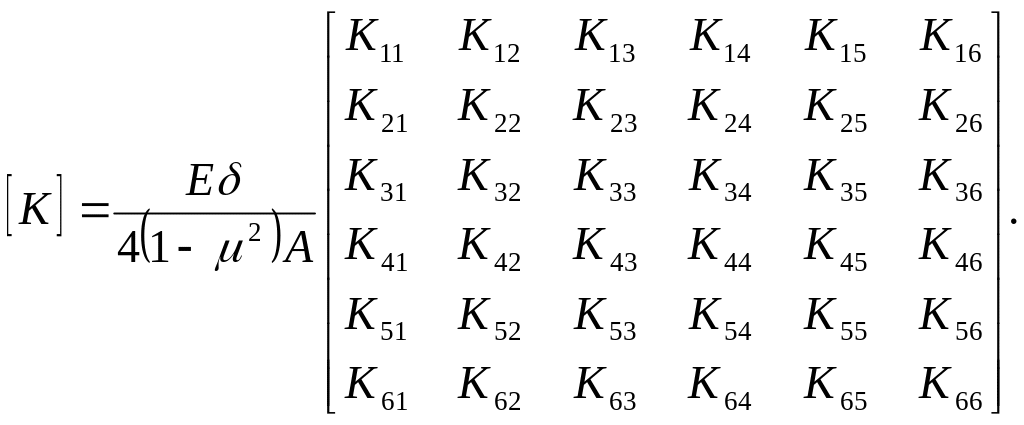
Элементы этой матрицы получаются решением матричного уравнения (14):

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

.

Глобальная матрица жесткости может быть найдена поэлементным суммированием матриц жесткости отдельных элементов и имеет размерность , где N - общее количество узлов разбиения.

Левую часть уравнения равновесия (13) составляет вектор силовых факторов , компоненты которого в количестве равны силам, действующим в узлах. Учет распределенной нагрузки производится равномерным ее распределением по узлам, расположенным на границе.