79.Решетчатые функции и z-преобразование решетчатой функции

1. Преобразователь аналог-код преобразует непрерывную функцию в решетчатую функцию . Из рис.3 видно, что приход от непрерывной функции к решетчатой может быть выполнен формальной заменой .

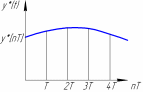
Рис.3. Определение решетчатой функции

2. Для решетчатых функций методы дифференциального и интегрального исчисления справедливые для непрерывных функций, непригодны. Дискретным аналогом производной для решетчатой функции является разность:

. (3)

Дискретным аналогом второй производной – является вторая разность:

(4)

Общая формула для разности любого порядка:

. (5)

Дискретным аналогом интеграла является сумма:

. (6)

3. Соотношения (3) и (6) имеют строгий физический смысл. Так формула (3) представляет отношение приращения функции на интервале к приращению аргумента Т и является приближенным значением производной. Формула (6) представляет вычисления интеграла методом прямоугольника.

4. Для дискретных систем, как и для непрерывных, широкое распространение получили онфаторные методы. Среди этих методов чаще используется метод Z-преобразований, т.к. его соотношения по структуре аналогичный соотношением для непрерывных систем при использовании преобразования Лапласа.

Z-преобразование решетчатой функции –это функция комплексного переменного F(z), определяемая соотношением:

(7)

5. Найдём связь между комплексными переменными ZиSдля чего рассмотрим формулу преобразования Лапласа:

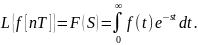(8)

Используя формулу прямоугольника, заменяем приближенное соотношения для вычисления интеграла правой части формулы (8):

(9)

Сравним правые части (7) и (9), получим:

(10)

Откуда связь между комплексными переменными ZиS будет выражаться соотношением:

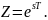(11)

80. Дискретная передаточная функция дискретного динамического звена

1)Под дискретным динамическим звеном понимается последовательное соединение непрерывного динамического и двух импульсных элементов, преобразующих непрерывный сигнал в последовательность импульсов соответствующей амплитуды и отстоящих друг от друга на величину Т, рис.4.

Рис.4. Дискретное динамическое звено

Полагаем что на вход дискретного ДЗ подан непрерывный сигнал . На выходе импульсного элемента ИЭ1 имеет место решетчатая функция . При подачи непрерывной части дискретного ДЗ последовательности импульсов на выходе будем иметь непрерывный сигнал , а на выходе импульсного элемента ИЭ2 – последовательность импульсов .

2)В непрерывных ДЗ связь между входным сигналом и выходным сигналом определяется интегралом Дюамеля:

, (12)

где – импульсная переходная функция ДЗ.

По аналогии для дискретного ДЗ имеем:

(13)

Суммирования в правой части (13) проводится до n. Так как значения решетчатой функции от отрицательного аргумента тождественно равно нулю, формулу (13) можно записать в виде:

(14)

Применив операцию Z-преобразования к обеим частям (14), получим:

. (15)

В правой части (15) от nзависит только величина , поэтому формула (15) запишется в виде:

. (16)

Докажем равенство:

. (17)

Применив к левой части равенства (17) операциюZ-преобразования, имеем:

(18)

Обозначим , тогда правая часть (18) может быть представлена в виде:

(19)

С учетом этого результата представим формулу (16) в виде:

(20)

Аналогично с непрерывными системами. Дискретной передаточной функцией дискретного ДЗ является отношение Z-преобразования решетчатой функции к Z-преобразованию решетчатой функции :

. (21)

Если для непрерывных динамических звеньев, в соответствии с отношением (21), передаточная функция равна Z-преобразованию решетчатой функции , соответствующей импульсной переходной функции непрерывной части дискретного динамического звена.

Дискретная передаточная функция дискретного ДЗ может быть получена следующим образом:

1)Находится передаточная функция W(S) непрерывной части дискретного ДЗ;

2)По таблицам преобразования Лапласа отыскиваются импульсная переходная функция непрерывной части дискретного ДЗ:

;

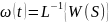3)С помощью замены t=nT осуществляется переход от непрерывной функции к решетчатой функции ;

4)По таблицам Z-преобразований находится дискретная передаточная функция дискретного динамического звена:

.