- •34. Динамическая нагруженность привода станка при пуске для эквивалентной трехмассовой системы [5,9].
- •35. Нагрузка на вал двухмассовой системы при пуске, максимальные значения коэффициента динамичности, нагрузка на вал при любых законах нагружения [5].
- •37. Вычисление частот собственных колебаний трехмассовой системы [5,9,3].
- •38. Понятие о нормальных формах колебаний [5].
- •44. Частотная (комплексная передаточная) функция, формулы амплитуди и фазы частотной характеристики.
- •45. Частотные характеристики линейных элементов системы и построение афчх, ачх и фчх.
- •47. Методика операторной формы записи дифференциальных уравнений и их решение методом операционного исчисления
- •47. Методика операторной формы записи дифференциальных уравнений и их решение методом операционного исчисления
- •48. Характерные особенности приводов станков в зависимости от их типов
- •54. Характеристики и передаточная функция дифференцирующего дз
- •55. Характеристики и передаточная функция интегрирующего дз
- •56. Характеристики и передаточная функция колебательного дз
- •57, 58 Единичная ступенчатая и переходная функции, Единичная импульсная ( -функция) и импульсная переходная функции. Связь -функции с единичной ступенчетой.
- •59. Связь между переходной и импульсной переходной функциями.
- •60. Связь переходной и передаточной функциями и обратно.
- •65. 2. Принявобозначение принимаем в виде
- •70. Логарифмические частотные характеристики лачх и лфчх.
- •78.Цифровые вычислительные устройства в контуре управления
- •79.Решетчатые функции и z-преобразование решетчатой функции
- •80. Дискретная передаточная функция дискретного динамического звена
- •81. Дискретная передаточная функция замкнутой системы с цифровой вычислительной машиной в контуре управления:
- •82. Устойчивость дискретных замкнутых систем автоматического управления
- •83. Динамический расчет шпиндельного узла методом начальных параметров
- •86. Способы улучшения характеристик упругих систем станков
- •87. Способы уменьшения потерь на трение, повышения плавности перемещения и позиционирования подвижных узлов.
70. Логарифмические частотные характеристики лачх и лфчх.
Учитывая связь пердаточной функции с импульсной переходной функцией, в соответствии с прямим изображением Лапласа, по формуле и выражении интеграла Фурье, частотная передаточная функция являеться изображением Фурье его импульсной переходной функции (функции веса) или иначе интегральным преобразованием Фурье:
 ,
,
где -
функциявеса.
-
функциявеса.
С другойсторонычастотнаяфункцияопределяетьсяамплитудой и фазой при еёпредставлении в виде комплексного числа:
 .
.
где A(w)- модуль частотной передаточной функции; u(w), v(w) – вещественная и мнимая систавляющая частотной передаточной функции.
При этом частотная передаточная функция:
 ,
где
,
где -
соответственно. Комплексноевыражениесигналов
на выходе и на входе, которые в свою
очередьсоответственноравны:
-
соответственно. Комплексноевыражениесигналов
на выходе и на входе, которые в свою
очередьсоответственноравны:
 ,
,
 .
.
Отношениесигналов к
к
 в видепоказательных функцій
непосредственноприводит к
выражениючастотнойпередаточнойфункции.
в видепоказательных функцій
непосредственноприводит к
выражениючастотнойпередаточнойфункции.
Прологарифмировавполучим:
 ,
гдевещественнаячасть – представляет
логарифм модуля
,
гдевещественнаячасть – представляет
логарифм модуля
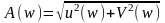 ,
а мнимая – здвиг фазысигнала на выходе
,
а мнимая – здвиг фазысигнала на выходе .
.
Таким образом, согласноформуле, логарифм частотной передаточной функции равен комплексному выражению вещественной части в виде логарифма модуля, а мнимая часть – в виде сдвига фазового угла на выходе.
Практически
целеобразно использование десятичных
логарифмов и по отдельности строить
логарифмическую амплитудно-частотную
и логарифмическую фазо-частотную
характеристики (ЛАЧХ, ЛФЧХ). Посредствам
десятичных логарифмов вещественную
часть можно подставить в виде:
 .
.
Эта величина имеет размерность в децебелах, Бел- логарифмическая единица, равняется 10 кратному увеличению мощности, тоесть 1бел-соответсвует увеличению мощьности в 10 раз, 2 бела –в 100раз, 3 бела- в 1000 раз и т.д. Децибел равен 0.1 бела.
Так
как
 характеризуетперемещение,
скорости, так, какмощности, то
увеличениемощности в 100 раз, согласноформуле
характеризуетперемещение,
скорости, так, какмощности, то
увеличениемощности в 100 раз, согласноформуле ,
соответствует 2 белам=20 децибелам.
Этимобьясняетьсяналичиемножителя 20 в
правой части формулы. В частности 1
децибел соответствуетизменениюамплитуды
в
,
соответствует 2 белам=20 децибелам.
Этимобьясняетьсяналичиемножителя 20 в
правой части формулы. В частности 1
децибел соответствуетизменениюамплитуды
в
 раз, чтопредставляетнеисчислительную
величину.
раз, чтопредставляетнеисчислительную
величину.
Для
построения ЛАЧХ и ЛФЧХ по оси абсцисс
откладивается учитывая частоту в
логарифмическом масштабе, т.е.
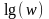 ,
которыйсоответствует частотаwв
рад/с.
,
которыйсоответствует частотаwв
рад/с.
По
оси ординат откладывается модуль
частотной передаточной функции в
децибелах и шкала является равномерной.
Ось абсцисс проходит через точку О дБ,
что соответсвует значению модуля
А(w)=1,
т.е.
 .
.
Удесятирениечастоты
по шкалеабсцисссоответствуютоднойдекаде
и приращениюшкалы на
 ,
рис.13. Кроме того, граду совка
шкалыабсциссможетвыполняться в октавах,
чтосоответствуетудвоениючастоты, т.е
,
рис.13. Кроме того, граду совка
шкалыабсциссможетвыполняться в октавах,
чтосоответствуетудвоениючастоты, т.е .
Тогда 1 октава равна 0.303 декады. При этом
шкала обозначается не в единицахчастоты,
а в единицах логарифма частоты,
чтоснижаетприемуществоприминениялогарифмических
шкал.
.
Тогда 1 октава равна 0.303 декады. При этом
шкала обозначается не в единицахчастоты,
а в единицах логарифма частоты,
чтоснижаетприемуществоприминениялогарифмических
шкал.
Достоинствологарифмических характеристик состоит в том, чтопроизведениесомножителейзаменяетсяихсуммированием. Согласно ЛАЧХ, какуравнениепрямой с угловымкоэфициентомнаклонаравным 20дб/с, изображается обрезками прямых линий с наклонами.
Так
при построении ЛАЧХ для частотной
характеристики равный постоянному
числу, т.е. при
 ,
по формуле
,
по формуле и на графикеэтопрямая паралельна оси
абсцисс (прямая 1) рис.13.
и на графикеэтопрямая паралельна оси
абсцисс (прямая 1) рис.13.
При
 по формуле
- 20lgwи
на графике – это прямая, проходящая
через точку с координатой
по формуле
- 20lgwи
на графике – это прямая, проходящая
через точку с координатой
 и
и
 иимеяотрицательныйнаклон
20дб/дек., т.к. каждоеудесятирениечастотывызывает
иимеяотрицательныйнаклон
20дб/дек., т.к. каждоеудесятирениечастотывызывает на 1 единицу, т.е. уменшение
на 1 единицу, т.е. уменшение на 20 дб, прямая 2, наклон 20дб/с≈6дб/октаву,
т.к
на 20 дб, прямая 2, наклон 20дб/с≈6дб/октаву,
т.к
Точка
пересечения прямой
 с осьюабсцисс, когда
с осьюабсцисс, когда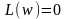 дБ, называютчастотойсреза ЛАЧХ и для
данногослучая
дБ, называютчастотойсреза ЛАЧХ и для
данногослучая ,
т.е, когда
,
т.е, когда . Откудаследует, что
и k
имеет туже фазочастоту, что и
. Откудаследует, что
и k
имеет туже фазочастоту, что и
 .
.

Рис.13 Построение ЛАЧХ: а) для частотной передаточной функции с , б) для .
Устойчивостьдинамическойсистемы
по логарифмическим частотам
xпрактическимопределяется
с использованиемкритериянейквиста.
Критической точка, где модуль АФЧХ рамен
1, соответствуетточкепересечения ЛАЧХ
с осьюабсцисс на частотесреза Точка пересечения АФЧХ с линей- π
соответствует фазовому здвигу 180º.
Замкнутая система считаетсяустойчивой,
корда на частоте
Точка пересечения АФЧХ с линей- π
соответствует фазовому здвигу 180º.
Замкнутая система считаетсяустойчивой,
корда на частоте ,
для которой ордината ЛАЧХ разомкнутой
системыотрицательная,
т.е.
,
для которой ордината ЛАЧХ разомкнутой
системыотрицательная,
т.е.
 ,
рис.14а. Еслиразомкнутая система устойчива,
ЛАЧХ пересекаетлинию- π несколько раз,
то ордината ЛАЧХ
при
,
рис.14а. Еслиразомкнутая система устойчива,
ЛАЧХ пересекаетлинию- π несколько раз,
то ордината ЛАЧХ
при
 в
последнейточкепересечения рис.14б.
в
последнейточкепересечения рис.14б.
Система неустойчива для случая показаного на рисунке 14в.
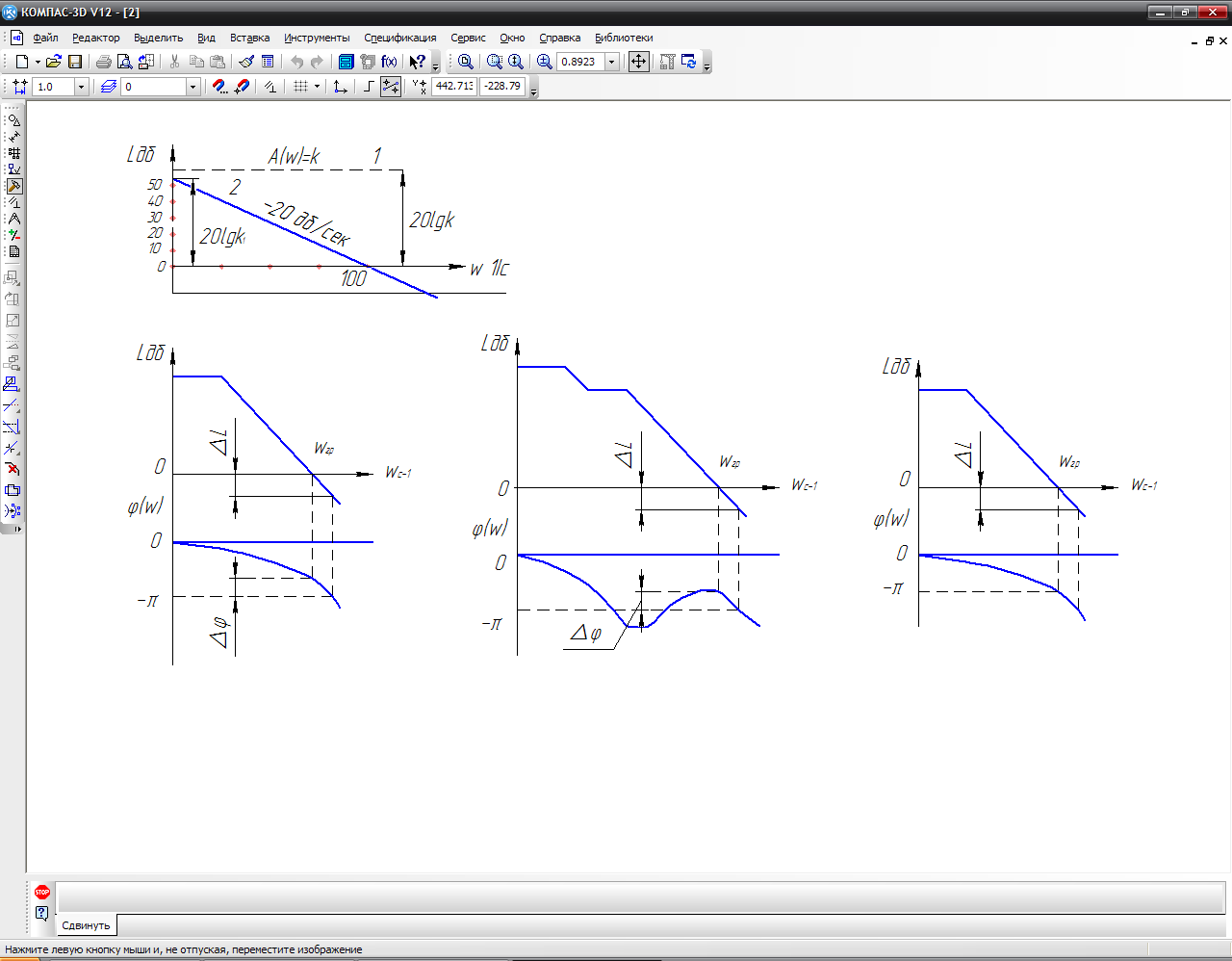 Рис.14
– ЛАЧХ И ЛФЧХ для оченки устойчивости
системы: а),б) – система устойчива; в)
–система неустойчива.
Рис.14
– ЛАЧХ И ЛФЧХ для оченки устойчивости
системы: а),б) – система устойчива; в)
–система неустойчива.
Запас
устойчивости системы по амплитуде фазе
оценивается отрезками Lи
φ как показано на рис.14. Запас устойчивости
по амплитуде оказывает на сколько
децибел необходимо увеличить коэфициент
усиления по частоте, соответствующей
фазовому сдвигу
чтобы
система стала устойчивой. Запас
устойчивости по фазе .
Условияудолетворительногокачестварегулирования
:
.
Условияудолетворительногокачестварегулирования
:
 .
. -для
систем САУ.
-для
систем САУ.
Последовательностьпостроения ЛАЧХ и некоторыеметодическиеуказания.
Определяетьсясопрягающиечастоты, в которыхграфикL(w) имеет идеомы. На оси абсцисс в логарифмическом масштабе откладывается значение сопряженных частот. Расчетные значения сопряжаемых частот определяется из соотношения
 ,
где Тi
– постоянная
времени соответствующего элемента
САУ.
,
где Тi
– постоянная
времени соответствующего элемента
САУ.Строится низкочастотная прямая ЛАЧХ для
 і наклоном - 20μ, гдеμ-число
интегрирующихзвеньев с главной цепи
системы.
Эта прямая при
і наклоном - 20μ, гдеμ-число
интегрирующихзвеньев с главной цепи
системы.
Эта прямая при
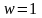 имеет
ординату
имеет
ординату
 ,
гдек-передаточныйкоэфициентсистемы.
,
гдек-передаточныйкоэфициентсистемы.НАклонпрямой ЛАЧХ относительнопредыдущегоучастка для каждойсопрягающейчастоты
 зависит
от типа динамическогозвена(для
дифференцирующегозвена от состовляющей
20дб/дек; для апериодического и
интегрирующего - 20дб/дек; для колебательного
– 40дб/дек.)
зависит
от типа динамическогозвена(для
дифференцирующегозвена от состовляющей
20дб/дек; для апериодического и
интегрирующего - 20дб/дек; для колебательного
– 40дб/дек.)Сдвиг фаз выходныхсигналовотносительновходных для ЛФЧХ в случаеапериодическогозвенасоставляющей -
 ;
для
идеального и реального дифференцирующих
звеньев, соответственно
;
для
идеального и реального дифференцирующих
звеньев, соответственно
 , для интегрирующего
, для интегрирующего
 ;
для колебательного
;
для колебательного
71.
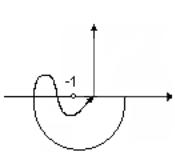
Лекция №11 Определение устойчивости по логарифмическим характеристикам. Критерий устойчивости Найквиста: В Wраз заменяем s на jω. Для нескольких значений ω рассчитываем точки комплексной плоскости и строим годограф. Если годограф не охватывает критическую точку (-1; j0), значит система устойчивая. Иначе – система неустойчивая.
|
Рисунок 2 Неустойчивая система Идея определения устойчивости системы по логарифмическим характеристикам базируется на критерии устойчивости Найквиста. |