17. Определитель второго порядка. Условие равенства нулю

Пусть дана квадратная таблица из четырех чисел , , , :

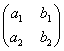. (1)

Число называется определителем второго порядка, соответствующего таблице (1). Этот определитель обозначается символом 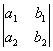; соотвественно имеем

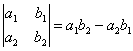. (2).

Числа , , , называются элементами определителя. Говорят, что элементы , лежат на главной диагонали определителя, , - на побочной. Таким образом, определитель второго порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях.

Свойства определителей второго порядка:

1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами.

2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину

3. Определитель с двумя одинаковыми строками и столбцами равен нулю.

4. Общий множитель всех элементов строки или столбца можно выносить за знак определителя; если все элементы какой-то строки или столбца равны 0, то и определитель равен 0.

5. Если к элементам какой либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины.

18. Определитель третьего порядка. Вычисление разложением по столбцу, по строке и по правилу треугольника.

Пусть дана квадратная таблица из девяти чисел , , , , , , , , :

. (1)

Определителем третьего порядка, соответствующим таблице (1), называется число, обозначаемое символом

и определяемое равенством

.

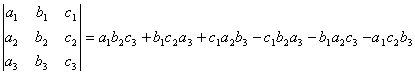Для квадратной матрицы третьего порядка формула вычисления определителя разложением по 1-ой строке имеет вид:

= - + .

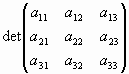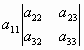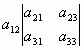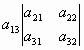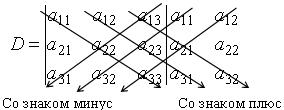
По правилу треугольника сначала перемножаются и складываются элементы, соединенными на схеме линиями

т.е. получаем сумму произведений: a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂.

Затем перемножаются и складываются элементы, соединенные на схеме

т.е. получаем другую сумму произведений a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂. И, наконец, чтобы вычислить определитель, из первой суммы вычитают вторую. Тогда окончательно получаем формулу вычисления определителя третьего порядка:

D=(a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂)-(a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂).

По правилу Саррюса к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в одном направлении и из нее вычитают сумму произведений элементов в другом направлении (см. схему):

19. Решение систем линейных уравнений по правилу Крамера

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

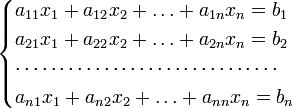
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

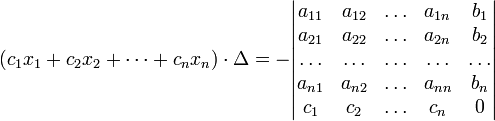
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом.