47. Несобственные интегралы. Определение сходимости
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
Предел a или b (или оба предела) являются бесконечными;
Функция f(x) имеет одну или несколько точек разрыва внутри интервала [a, b].
Несобственные интегралы I рода
Пусть f(x) определена
и непрерывна на множестве от
и
.
Тогда:
Если
,
то используется обозначение
и
интеграл называется несобственным
интегралом Римана первого рода. В этом
случае
называется
сходящимся.
Если не существует
конечного
(
или
),
то интеграл
называется
расходящимся к
,
или просто расходящимся.
Пусть f(x) определена
и непрерывна на множестве от
и
.
Тогда:
Если
,
то используется обозначение
и
интеграл называется несобственным
интегралом Римана первого рода. В этом
случае
называется
сходящимся.
Если не существует
конечного
(
или
),
то интеграл
называется
расходящимся к
,
или просто расходящимся.
Если функция f(x) определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
,
где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
Несобственные интегралы II рода
Пусть f(x) определена
на (a,b], терпит бесконечный разрыв в точке
x=a и
.
Тогда:
Если
,
то используется обозначение
и
интеграл называется несобственным
интегралом Римана второго рода. В этом
случае интеграл называется сходящимся.
Если
или
,
то обозначение сохраняется, а
называется
расходящимся к
,
или просто расходящимся.
Пусть f(x) определена
на [a,b) , терпит бесконечный разрыв при
x=b и
.
Тогда:
Если
,
то используется обозначение
и
интеграл называется несобственным
интегралом Римана второго рода. В этом
случае интеграл называется сходящимся.
Если
или
,
то обозначение сохраняется, а
называется
расходящимся к
,
или просто расходящимся.
Если функция f(x)
терпит разрыв во внутренней точке c
отрезка [a;b], то несобственный интеграл
второго рода определяется формулой:
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
Пример
Критерий Коши
1. Пусть f(x) определена
на множестве от
и
.
Тогда
сходится
2. Пусть f(x) определена
на (a,b] и
.
Тогда
сходится
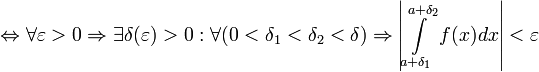
Абсолютная сходимость:
Интеграл
называется
абсолютно сходящимся, если
сходится.
Если
интеграл сходится абсолютно, то он
сходится.
Условная сходимость:
Интеграл
называется
условно сходящимся, если
сходится,
а
расходится.
48. Понятие о дифференциальных равнениях
Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y'(x),y''(x),...,yn(x) до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
или
,
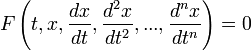где
—
неизвестная функция
(возможно, вектор-функция;
в таком случае часто говорят о системе
дифференциальных уравнений), зависящая
от переменной времени
,
штрих означает дифференцирование по
.
Число
называется
порядком дифференциального уравнения.
Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:
,
где
—
независимые переменные, а
—
функция этих переменных.
49. Уравнение
,
его общее и частные решения
- общее решение
дифференциального уравнения.
Зная общее решение однородного дифференциального уравнения и любое частное решение неоднородного уравнения, можно получить общее решение неоднородного уравнения в виде суммы общего решения однородного уравнения и частного решения неоднородного.