
- •Высказываниящ, операции над высказываниями: отрицание, «и», «или», «следует»
- •Построение отрицаний
- •Утверждение «следует», «обратное», «противоположное». Доказательство от противного, необходимое и достаточное условия
- •4. Множества, операции над множествами
- •5 Конструкция высказывания с кванторами существования и всеобщности, построение отрицаний
- •6. Координаты точки на прямой, расстояние между двумя точками, деление отрезка в данном соотношении
- •7. Координаты точки на плоскости, расстояние между двумя точками, деление отрезка в данном соотношении
- •8. График уравнения. Уравнение кривой. Примеры: график линейного уравнения, уравнение окружности
- •9. Уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку. Условие параллельности и перпендикулярности прямых.
- •10. Уравнение прямой, проходящей через две точки
- •11. Вектор на плоскости, координаты вектора, длина вектора. Операции над векторами. Орт вектора. Условие параллельности векторов
- •12. Скалярное произведение векторов, условие перпендикулярности
- •13. Координаты точки в трехмерном пространстве, векторы в трехмерном пространстве
- •14. Уравнение прямой и плоскости в трехмерном пространстве
- •15. Векторы. Линейная комбинация, линейная зависимость и независимость векторов
- •16. Матрицы. Сложение, умножение, умножение на вектор
- •17. Определитель второго порядка. Условие равенства нулю
- •18. Определитель третьего порядка. Вычисление разложением по столбцу, по строке и по правилу треугольника.
- •19. Решение систем линейных уравнений по правилу Крамера
- •20. Метод Гаусса решения систем линейных уравнений
- •21. Числовая прямая, модуль числа и его геометрический смысл, неравенство треугольника
- •22. Функция, область определения, график. Основные элементарные функции и их графики
- •23. Преобразования графиков функций – сдвиг, растяжение
- •24. Последовательность. Примеры
- •25. Предел переменной величины. Предел последовательности. Предел функции. Бесконечно малая величина, последовательность, функция.
- •26. Бесконечно большая функция, последовательность, величина
- •27. Теоремы об арифметических операциях над пределами
- •28. Сравнение бесконечно малых величин. Понятие главной части. Сравнение скорости роста степенной, показательной и логарифмической функций.
- •29. Определение производной функции в точки, ее геометрический смысл
- •30. Производные основных элементарных функций
- •31. Производная константы, суммы, произведения, отношения. Производная сложной функции.
- •32. Дифференциал функции в точке. Формула Тейлора
- •33. Применение формулы Тейлора к приблизительным вычислениям
- •34. Условие монотонности функции на промежутке
- •35. Условие экстремума функции в точке
- •36. Выпуклость функции на промежутке, условие выпуклости, точки перегиба
- •37. Схема построения графиков функций
- •38. Функция нескольких переменных. Частные производные. Необходимые условия экстремума функции нескольких переменных
- •39. Получение эмпирических формул по методу наименьших квадратов. Построение линейной эмпирической зависимости по методу наименьших квадратов.
- •40. Первообразная функции на промежутке
- •41. Неопределенный интеграл и его основные свойства
- •42. Метод разложения. Примеры
- •43. Метод подстановки. Примеры
- •44. Определенный интеграл. Определение, физическая и геометрическая
- •45. Формула Ньютона-Лейбница
- •46. Вычисление площадей с помощью определенного интеграла
- •47. Несобственные интегралы. Определение сходимости
- •48. Понятие о дифференциальных равнениях
- •50. Понятие о средних. Среднее арифметическое, квадратичное, геометрическое, гармоническое и их определяющие свойства. Неравенства между средними.
29. Определение производной функции в точки, ее геометрический смысл
Пусть
в некоторой окрестности
точки
![]() определена
функция
определена
функция
![]() Производной
функции f
в точке x0
называется предел,
если он существует,
Производной
функции f
в точке x0
называется предел,
если он существует,
![]()
Общепринятые обозначения производной функции y = f(x) в точке x0:
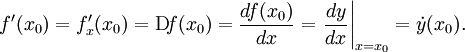
Производная f'(x0) функции f в точке x0, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x0 тогда и только тогда, когда её производная в этой точке существует и конечна:
![]()
Для дифференцируемой в x0 функции f в окрестности U(x0) справедливо представление
f(x)
= f(x0)
+ f'(x0)(x
− x0)
+ o(x
− x0)
при
![]()
Если
функция
![]() имеет
конечную производную в точке x0,
то в окрестности U(x0)
её можно приблизить линейной
функцией
имеет
конечную производную в точке x0,
то в окрестности U(x0)
её можно приблизить линейной
функцией
![]()
Функция fl называется касательной к f в точке x0. Число f'(x0) является угловым коэффициентом или тангенсом угла наклона касательной прямой.
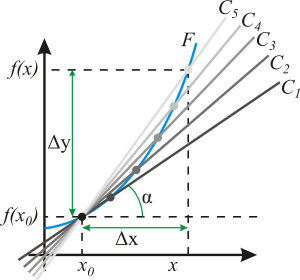
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
30. Производные основных элементарных функций
![]()
![]()
![]()
![]()
![]() когда
когда
![]() и
и
![]() определены,
определены,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
31. Производная константы, суммы, произведения, отношения. Производная сложной функции.
Производная
константы:
![]()
Производная суммы:
![]()
Произодная
произведения:
![]()
Производная
отношения:
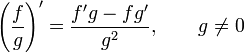
Сложная
функция (композиция
функций,
суперпозиция
функций)
обозначается
![]() или
или
![]() .
.
Производная композиции равна:
![]()
Если необходимо взять производную от композиции трех и более функций, то последовательно применяем указанное выше правило. Например,
![]()
32. Дифференциал функции в точке. Формула Тейлора
Функция
![]() называется
дифференцируемой в точке
называется
дифференцируемой в точке
![]() ,
предельной для множества E, если ее
приращение Δf(x0), соответствующее
приращению аргумента x, может быть
представлено в виде
,
предельной для множества E, если ее
приращение Δf(x0), соответствующее
приращению аргумента x, может быть
представлено в виде
Δf(x0) = A(x0)(x - x0) + ω(x - x0), (1)
где ω(x - x0) = о(x - x0) при x → x0.
Отображение
![]()
![]() ,
называется дифференциалом функции f в
точке x0, а величина A(x0)h - значением
дифференциала в этой точке.
,
называется дифференциалом функции f в
точке x0, а величина A(x0)h - значением
дифференциала в этой точке.
Для значения дифференциала функции f принято обозначение df или df(x0), если требуется знать, в какой именно точке он вычислен. Таким образом, df(x0) = A(x0)h.
Разделив в (1) на x
- x0 и устремив x к x0, получим A(x0) = f'(x0).
Поэтому
![]() имеем
имеем
df(x0) = f'(x0)h. (2)
Сопоставив (1) и (2), видим, что значение дифференциала df(x0) (при f'(x0) ≠ 0) есть главная часть приращения функции f в точке x0, линейная и однородная в то же время относительно приращения h = x - x0.
Если скалярные величины u и v дифференцируемы, то:
а)
![]()
![]() ;
;
б)
![]()
![]() ;
;
в)
![]()
![]() ;
;
г)
![]()
![]() ;
;
Если вектор-функции u и v дифференцируемы, то
а) d(u ± v) = du ± dv;
б) d(u, v) = (du, v) + (u, dv);
в) d(λu) = udλ + λdu (λ - скалярная функция).
Рассмотрим функцию y = f(x), определенную в U(a) и имеющую производную до n – ого порядка в самой точке a.
Требуется найти такой многочлен Tn (x) степени меньшей, или равной n, значение которого в точке a совпадает со значением функции f(x), а все его производные до n – ого порядка включительно в точке а совпадают с производными функции f(x).
![]() (1)
(1)
Этот многочлен будет близок к функции f(x) в U(a).
Будем искать его в виде:
![]() (2)
(2)
т.е. по степеням разности (x - a) с неопределенными коэффициентами.
Коэффициенты а0, а1, а2, …, аn определим из условий (1):
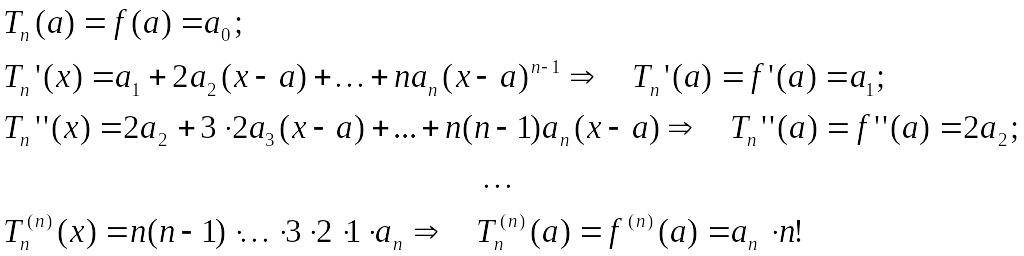
Следовательно,
![]() (3)
(3)
Тогда многочлен Tn (x) принимает вид:
![]() (4)
(4)
Многочлен (4) называется многочленом Тейлора для данной функции f(x) в точке а. Многочлен Тейлора является приближением функции f(x) в U(a).
