13. Координаты точки в трехмерном пространстве, векторы в трехмерном пространстве

Декартовыми прямоугольными координатами точки P в трехмерном пространстве называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до трех взаимно перпендикулярных координатных плоскостей или, что то же, проекции радиус-вектора r точки P на три взаимно перпендикулярные координатные оси.

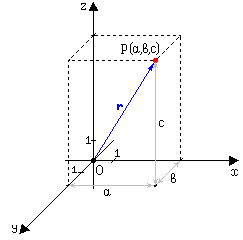
Координаты x, y, z называются соответственно абсциссой, ординатой и аппликатой.

Вектор в трехмерном пространстве определяется тремя координатами p(x, y, z).

Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа . В применении к любым векторам х, у, z и любым числам a, b эти правила удовлетворяют следующим условиям:

1. х + у = у + х (перестановочность сложения); 2) (х + у) + z = x + (y + z) (ассоциативность сложения); 3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x; 4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0, 5) 1 · х = х, 6) a(bx) = (ab) х (ассоциативность умножения); 7) (a + b) х = aх + bх (распределительное свойство относительно числового множителя); 8) a(х + у) = aх + aу (распределительное свойство относительно векторного множителя).

14. Уравнение прямой и плоскости в трехмерном пространстве

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0                                        (1)

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (1), которое называется уравнением плоскости.

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A ₁ x + B ₁ y + C ₁ z + D ₁ = 0, A ₂ x + B ₂ y + C ₂ z + D ₂ = 0;              (2)

2) двумя своими точками M ₁ (x ₁, y ₁, z ₁ ) и M ₂ (x ₂, y ₂, z ₂ ), тогда прямая, через них проходящая, задается уравнениями:

= ;                                       (3)

3) точкой M ₁ (x ₁, y ₁, z ₁ ), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

.                                        (4)

Уравнения (4) называются каноническими уравнениями прямой.

Вектор a называется направляющим вектором прямой.

Параметрические уравнения прямой получим, приравняв каждое из отношений (4) параметру t:

x = x ₁ + mt , y = y ₁ + nt , z = z ₁ + р t .                              (5)

Решая систему (2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой :

x = mz + a, y = nz + b.                                       (6)

От уравнений (6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

.

От общих уравнений (2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [ n ₁, n ₂ ], где n ₁ (A ₁, B ₁, C ₁ ) и n ₂ (A ₂, B ₂, C ₂ ) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система

равносильна системе ; такая прямая перпендикулярна к оси Ох.

Система  равносильна системе x = x ₁, y = y ₁ ; прямая параллельна оси Oz.