6. Координаты точки на прямой, расстояние между двумя точками, деление отрезка в данном соотношении

Прямая с выбранным на ней началом отсчета, единичным отрезком и направлением называется координатной прямой. Число, показывающее положение точки на прямой, называют координатой этой точки

Расстояние d между точками A(x₁) и B(x₂) на прямой:

Если точка М(x) лежит на прямой, проходящей через две данные точки

( ) и ( ), и дано отношение , в котором точка М делит отрезок , то координата точки М определяется по формуле ,.

Если точка М является серединой отрезка , то ее координата определяется по формуле .

7. Координаты точки на плоскости, расстояние между двумя точками, деление отрезка в данном соотношении

Координаты точки записываются в скобках рядом с названием точки, причем всегда на первом месте в прямоугольной системе координат записывается абсцисса точки, а на втором - ее ордината. Например, если x₁ - абсцисса точки A, а y₁ - ее ордината, то это записывается так: A(x₁, y₁).

У точки, лежащей на оси абсцисс, ордината равна нулю; у точки, лежащей на оси ординат, абсцисса равна нулю. Обе координаты начала координат равны нулю.

Расстояние d между точками A(x₁, y₁) и B(x₂, y₂) плоскости определяется по формуле:

Если точка М(x; y) лежит на прямой, проходящей через две данные точки ( , ) и ( , ), и дано отношение , в котором точка М делит отрезок , то координаты точки М определяются по формулам , .

Если точка М является серединой отрезка , то ее координаты определяются по формулам , .

8. График уравнения. Уравнение кривой. Примеры: график линейного уравнения, уравнение окружности

В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y)=0. При этом на функцию F должны быть наложены ограничения так, чтобы, с одной стороны, это уравнение имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло “куска плоскости”. Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, cуть прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.

График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты — соответствующими значениями функции y.

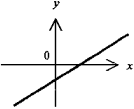Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)

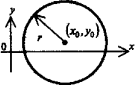Круг с центром в точке (x_o, y_o) радиуса r. (x-x_o)² + (y-y_o)² = r²

9. Уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку. Условие параллельности и перпендикулярности прямых.

Прямая линия, пересекающая ось Oy в точке и образующая угол с положительным направлением оси Ox: Уравнение прямой с угловым коэффициентом разрешено относительно текущей координаты y.

Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.

Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.   

В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.