Границы применения сил, классификация Прямые и обратные задачи механики. Начальные и граничные условия.

Прямая задача механики – по виду движения определить действующую на тело силу. Обратная задача механики – по заранее измеренной силе определить характер движения

Начальные и граничные условия

В теории дифференциальных уравнений, начальные и граничные условия — дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой области соответственно.

Обычно дифференциальное уравнение имеет не одно решение, а целое их семейство. Начальные и граничные условия позволяют выбрать из него одно, соответствующее реальному физическому процессу или явлению.

Пример

Уравнение   описывает движение тела в поле земного тяготения. Ему удовлетворяет любая квадратичная функция вида y(t) = − gt² / 2 + at+ b, где a,b — произвольные числа. Для выделения конкретного закона движения необходимо указать начальную координату тела и его скорость, то есть начальные условия.

Энергия и работа. (теорема о Ек)

Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах.

Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии.

Работа и Энергия

Термин "работа" в механике имеет два смысла: работа как процесс, при котором сила перемещает тело, действуя под углом, отличном от 90°; работа - физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением:

А = Fs cos a.

Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos а = 0). Единицей работы в СИ служит джоуль (Дж).

1 джоуль - это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы. Для определения быстроты совершения работы вводят величину "мощность".

Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:

Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт - мощность, при которой совершается работа в 1 Дж за 1 секунду.

Рассмотрим действие на тело некоторой постоянной силы F. На участке пути s будет произведена работа А. В результате у тела изменится скорость:

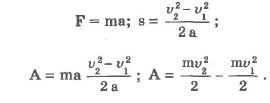
Величину   для материальной точки называют кинетической энергией тела.

Кинетическая энергия - энергия движения, ею обладают все движущиеся тела. Эта величина является относительной, то есть она изменяется в зависимости от выбранной системы отсчета.

Кроме этого вида механической энергии, существует и другой ее вид - потенциальная энергия. Рассмотрим систему двух взаимодействующих тел. Например, тела, поднятого над Землей, и саму Землю.

Работа силы тяжести при перемещении тела на отрезке |h₁ - h₂| будет равна:

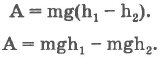
Величину mgh в соответствующей точке, которая расположена на высоте h, называют потенциальной энергией тела, находящегося в поле тяжести.

Из предыдущего уравнения вытекает, что работа не зависит от траектории движения в доле силы тяжести, а определяется лишь изменением высоты.

Потенциальная энергия характеризует и другие взаимодействующие тела. Так, потенциальной энергией обладает сжатая пружина:

где k - модуль упругости, х - смещение от положения равновесия.

Потенциальная энергия, как и кинетическая, является величиной относительной, поскольку и высота, и смещение зависят от выбора точки отсчета.

Теорема о кинетической энергии:

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

Физический смысл кинетической энергии:

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.