Энергия незатухающего колебательного движения Гармонический осциллятор

Консервативный гармонический осциллятор

В качестве модели консервативного гармонического осциллятора возьмём груз массы  , закреплённый на пружине жёсткостью  .

Пусть   — это смещение груза относительно положения равновесия. Тогда, согласно закону Гука, на него будет действовать возвращающая сила:

Используя второй закон Ньютона, запишем

Обозначая   и заменяя ускорение   на вторую производную от координаты по времени  , напишем:

Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Коэффициент ω₀ называют циклической частотой осциллятора. (Здесь имеется в виду круговая частота, измеряющаяся в радианах в секунду. Чтобы перевести её в частоту, выражающуюся в Герцах, надо разделить круговую частоту на 2π)

Будем искать решение этого уравнения в виде:

Здесь   — амплитуда,   — частота колебаний (пока не обязательно равная собственной частоте),   — начальная фаза.

Подставляем в дифференциальное уравнение.

Амплитуда сокращается. Значит, она может иметь любое значение (в том числе и нулевое — это означает, что груз покоится в положении равновесия). На синус также можно сократить, так как равенство должно выполняться в любой момент времени t. И остаётся условие на частоту колебаний:

Отрицательную частоту можно отбросить, так как произвол в выборе этого знака покрывается произволом выбора начальной фазы.

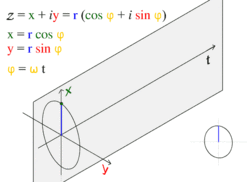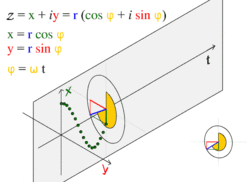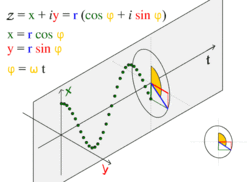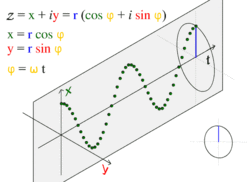
движение по кругу и движение гармоническое

Общее решение уравнения записывается в виде:

,

где амплитуда A и начальная фаза   — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям (начальному положению груза и его начальной скорости).

Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой.

Сложение колебаний одного направления и биений

Сложим гармонич. колебания одного направления и одинаковой частоты и построим векторные диаграммы этих колебаний 

Т.к. векторы А1 , А2 -вращаются с одинаковой угловой скоростью, то разность фаз будет постоянной.  . В этом выражении амплитуда А и начальная фаза  задаются соотношениями 

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой что и складываемые колебания. Амплитуда зависит от разности фаз.

В результате сложения колебаний мало отличающихся по частоте получаются колебания с периодически меняющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонич. колебаний с близкими частотами, наз. биениями.

Период биений 

Амплитуда биений 

Частота биений 

Сложение взаимно перпендикулярных колебаний. Фигура Лиссажу.

Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде   (1)  где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как      и заменяя во втором уравнении   на   и   на   , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:   (2)  Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.  Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес:  1) α = mπ (m=0, ±1, ±2, ...). 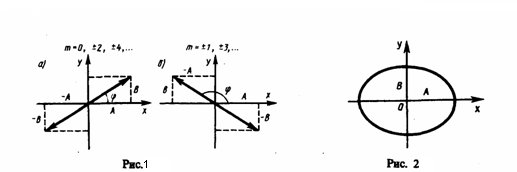В этом случае эллипс становится отрезком прямой   (3)  где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой , которое совершается вдоль прямой (3), составляющей с осью х угол . В этом случае имеем дело с линейно поляризованными колебаниями;  2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае уравнение станет иметь вид   (4)  Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями иликолебаниями, поляризованными по кругу. 

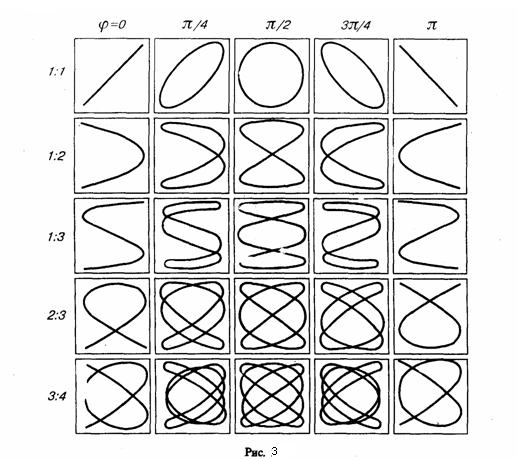
Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний. На рис. 3 даны фигуры Лиссажу для различных соотношений частот (даны слева) и разностей фаз (даны вверху; разность фаз равна φ).  Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, которые параллельны осям координат. По виду фигур можно найти неизвестную частоту по известной или найти отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко применяемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.