
- •Механика Кинематика криволинейного движения
- •Скорость и ускорение. Нормальное и тангенсальное.
- •Полное ускорение
- •Кривизна траектории.
- •Вращательное движение
- •Радиус вектор
- •Угловая скорость, ускорение
- •Зависимость угла скорости и угла поворота от времени.
- •Поступательное вращательное движение
- •Динамика Законы Ньютона
- •Сила как мера взаимодействия тел.
- •Поле Сил Силовые поля
- •Электростатическое поле (поле неподвижных зарядов)
- •Гравитационное поле
- •Электромагнитное поле, постоянное во времени (поле постоянных токов)
- •Электромагнитное поле (общий случай)
- •Границы применения сил, классификация Прямые и обратные задачи механики. Начальные и граничные условия.
- •Энергия и работа. (теорема о Ек)
- •Потенциальная энергия, как энергия в-я.
- •Системы изолированные и неизолированные.
- •Диссипация энергии в диссипативной системе
- •Работа переменной силы.
- •Работа и энергия в поле тяготения
- •Общие характеристики гравитационного поля.
- •Напряженность и потенциал гравитационного поля.
- •Гравитационный потенциал и уравнения движения
- •Связь потенциальной энергии и силы
- •Потенциальные кривые и энергетические уровни
- •Импульс (II закон Ньютона с использованием импульса).
- •Закон сохранения импульса
- •Вращательное движение
- •Момент силы.
- •Момент импульса.
- •Момент инерции
- •Осевые моменты инерции некоторых тел
- •Теорема Штейнера
- •[Править]Вывод
- •[Править]Пример
- •Основное уравнение динамики вращательного движения
- •Зако́н сохране́ния моме́нта
- •Гироскопический эффект
- •Кинетическая энергия вращающегося тела
- •Работа при вращательном движении
- •Общий случай плоского движения
- •Основное свойство плоского движения.
- •Сравнительный характер поступательного и вращательного движения.
- •Колебательные движения
- •Смещение, скорость, ускорение, фаза, начальная фаза колебательного движения.
- •Энергия незатухающего колебательного движения Гармонический осциллятор
- •Сложение колебаний одного направления и биений
- •Сложение взаимно перпендикулярных колебаний. Фигура Лиссажу.
- •Математический маятник
- •Физический маятник(приведенная длина, точка качения и их св-ва, вывод формулы периода).
- •[Править]Вычисление
- •Затухающие колебания(логарифмический декремент, 4 подхода к определению добротности)
- •Вынужденные колебания
- •Консервативный гармонический осциллятор
- •II закон Ньютона к поступательному, вращательному, колебательному движению.
- •Теория относительности
- •Следствия из постулатов сто
- •1. Относительность одновременности событий
- •2. Относительность промежутков времени
- •3. Относительность расстояний
- •4. Сложение скоростей в сто
- •5. Закон Ньютона в релятивистской форме
- •6. Связь между энергией и массой
- •Молекулярная физика Адиабатический процесс
- •Физический смысл адиабатического процесса
- •Адиабата Пуассона
- •Политропный процесс
- •Теорема Больцмана
- •[Править]h-теорема
- •Молекулярная теплоемкость газа.
- •Теплоёмкость для различных состояний вещества
- •Термодинамика Первое начало термодинамики
- •[Править]Частные случаи
- •Работа газа при изопроцессах
- •Молярная и удельная теплоемкость газа.
- •II начало термодинамики
- •Ограничения
- •Обратимые и необратимые процессы
- •Квазистатический процесс Квазистатический процесс
- •Значение квазистатических процессов
- •Виды квазистатических процессов
- •Тепловые, холодильные машины.(их кпд) Цикл Карно.
- •Кпд тепловой машины Карно
- •Приведенная теплота и теорема Клаузиса
- •Энтропия
- •Изменение энтропии при квазистопическом процессе.
- •Энтропия в изолированной системе
- •Макро и микро состояния.
- •Термодинамическая вероятность состояний
- •Эргодическая гипотеза Статистическое толкование энтропии
- •Теорема Нерста
- •Параметрическая формула и распределение Больцмана
- •Распределение Максвелла Реальные газы
- •Уравнение Ван-дер-Ваальса
- •Уравнение состояния
- •Внутренняя энергия газа Ван-дер-Ваальса
- •Явление переноса
- •Эффективное сечение
- •Число столкновений и средняя длина свободного пробега молекул в газах
Эффективное сечение
Эффективное
сечение–
мера вероятности столкновения
микрообъектов (атомов, ядер и частиц) в
виде эффективной площади их поперечного
сечения. Это основная величина,
характеризующая вероятности столкновений
(реакций) в микромире.
Пусть поток
одинаковых частиц пронизывает объём
пространства кубической формы с длиной
ребра 1 см, внутри которого в качестве
мишени находится одно атомное ядро (или
одна какая-либо частица). Местоположение
этого ядра (или частицы) внутри кубика
не имеет значения. Поток частиц падает
на одну из граней этого кубика под углом
90о,
причём в единицу времени (1 с) падает j
частиц однородно распределенных в
пространстве (j – плотность потока
частиц и имеет размерность см-2с-1).
Других частиц помимо тех, которые
бомбардируют кубик, нет. Из каждых j
частиц с ядром взаимодействует N частиц.
Поэтому численно вероятность взаимодействия
отдельной частицы с ядром равна N/j.
Именно это отношение с учетом его
размерности и называют эффективным
сечением ![]() ,
т.е.
=
N/j. Очевидно ? имеет размерность площади
(см2).
,
т.е.
=
N/j. Очевидно ? имеет размерность площади
(см2).
 К
понятию “эффективное сечение”
К
понятию “эффективное сечение”
Поясним
происхождение словосочетания “поперечное
эффективное сечение”. При механическом
соударении двух шаров, из которых один
покоится внутри единичного кубического
объёма, а о другом известно лишь то, что
он падает нормально на грань этого
кубика и имеет размеры незначительные
по сравнению с размерами покоящегося
шара, вероятность соударения шаров
численно равна площади поперечного
сечения s
= ![]() R2 покоящегося
шара, где R - радиус шара-мишени, т.е. в
данном случае
=
s = p R2.
Для
взаимодействий, не являющихся механическими
(контактными),
-
эффективная площадь, характеризующая
вероятность конкретного процесса. Она
может быть как больше геометрической
площади мишени (например, кулоновское
взаимодействие), так и меньше неё (слабое
взаимодействие).
Эффективное сечение
измеряют в барнах (б). 1 б = 10- 24 см2,
что примерно соответствует поперечной
геометрической площади ядра.
R2 покоящегося
шара, где R - радиус шара-мишени, т.е. в
данном случае
=
s = p R2.
Для
взаимодействий, не являющихся механическими
(контактными),
-
эффективная площадь, характеризующая
вероятность конкретного процесса. Она
может быть как больше геометрической
площади мишени (например, кулоновское
взаимодействие), так и меньше неё (слабое
взаимодействие).
Эффективное сечение
измеряют в барнах (б). 1 б = 10- 24 см2,
что примерно соответствует поперечной
геометрической площади ядра.
Число столкновений и средняя длина свободного пробега молекул в газах
Обозначим ![]() –
длина свободного пробега молекулы.
–
длина свободного пробега молекулы.
Медленность явлений переноса, например диффузии ароматических веществ – «распространение запаха», - при относительно высокой скорости теплового движения молекул (103 м/с) объясняется столкновениями молекул. Молекула газа время от времени сталкивается с другими молекулами. В момент столкновения молекула резко изменяет величину и направление скорости своего движения. Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега. Средняя длина свободного пробега равна:
|
|
|
|
где ![]() –
средняя скорость теплового движения,
τ – среднее время между двумя
столкновениями. Именно
–
средняя скорость теплового движения,
τ – среднее время между двумя
столкновениями. Именно ![]() -
средняя длина свободного пробега нас
интересует (рис. 3.1).
-
средняя длина свободного пробега нас
интересует (рис. 3.1).
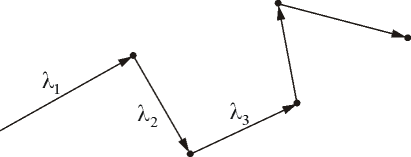 Рис.
3.1
Рис.
3.1
Модель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между собой только при столкновении. Обозначим σ – эффективное сечение молекулы, т.е. полное поперечное сечение рассеяния, характеризующее столкновение между двумя молекулами (рис. 3.2).
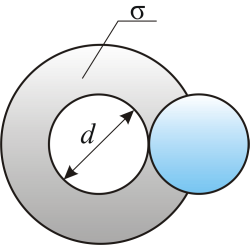 Рис.
3.2
Рис.
3.2
![]() –
площадь,
в которую не может проникнуть центр
любой другой молекулы. Здесь
–
площадь,
в которую не может проникнуть центр
любой другой молекулы. Здесь ![]() –
диаметр молекулы.
–
диаметр молекулы.
За одну секунду молекула проходит путь, равный средней арифметической скорости . За ту же секунду молекула претерпевает ν столкновений. Следовательно,
|
|
|
3.2.1 |
Подсчитаем число столкновений ν.
Вероятность столкновения трех и более молекул бесконечно мала.
Предположим, что все молекулы застыли, кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d (рис. 3.3).
 Рис.
3.2
Рис.
3.2
Путь,
который пройдет молекула за одну секунду,
равен длине цилиндра ![]() .
Умножим объём цилиндра
.
Умножим объём цилиндра ![]() на
число молекул в единице объёма n,
получим среднее число столкновений в
одну секунду:
на
число молекул в единице объёма n,
получим среднее число столкновений в
одну секунду:
|
|
|
3.2.1 |
На самом деле, все молекулы движутся (и в сторону, и навстречу друг другу), поэтому число соударений определяется средней скоростью движения молекул относительно друг друга.
По закону сложения случайных величин
|
|
|
(3.2.1) |
А
так как средняя длина свободного
пробега ![]() то
получим:
то
получим:
|
|
|
(3.2.2) |
Уравнение состояния идеального газа позволяет нам выразить n через давление P и термодинамическую температуру Т.
Так
как ![]() ,
то есть
,
то есть ![]() то
то
|
|
|
(3.2.3) |
Таким образом, при заданной температуре средняя длина свободного пробега обратно пропорциональна давлению Р:
|
|
|
|
Например, при d =
3 Å = 3×10-10 м, Р =
1 атм., Т =
300 К,![]() а,
т.к.
а,
т.к. ![]() ,
то
,
то ![]() столкновений.
столкновений.
