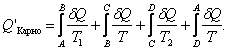- •Механика Кинематика криволинейного движения
- •Скорость и ускорение. Нормальное и тангенсальное.
- •Полное ускорение
- •Кривизна траектории.
- •Вращательное движение
- •Радиус вектор
- •Угловая скорость, ускорение
- •Зависимость угла скорости и угла поворота от времени.
- •Поступательное вращательное движение
- •Динамика Законы Ньютона
- •Сила как мера взаимодействия тел.
- •Поле Сил Силовые поля
- •Электростатическое поле (поле неподвижных зарядов)
- •Гравитационное поле
- •Электромагнитное поле, постоянное во времени (поле постоянных токов)
- •Электромагнитное поле (общий случай)
- •Границы применения сил, классификация Прямые и обратные задачи механики. Начальные и граничные условия.
- •Энергия и работа. (теорема о Ек)
- •Потенциальная энергия, как энергия в-я.
- •Системы изолированные и неизолированные.
- •Диссипация энергии в диссипативной системе
- •Работа переменной силы.
- •Работа и энергия в поле тяготения
- •Общие характеристики гравитационного поля.
- •Напряженность и потенциал гравитационного поля.
- •Гравитационный потенциал и уравнения движения
- •Связь потенциальной энергии и силы
- •Потенциальные кривые и энергетические уровни
- •Импульс (II закон Ньютона с использованием импульса).
- •Закон сохранения импульса
- •Вращательное движение
- •Момент силы.
- •Момент импульса.
- •Момент инерции
- •Осевые моменты инерции некоторых тел
- •Теорема Штейнера
- •[Править]Вывод
- •[Править]Пример
- •Основное уравнение динамики вращательного движения
- •Зако́н сохране́ния моме́нта
- •Гироскопический эффект
- •Кинетическая энергия вращающегося тела
- •Работа при вращательном движении
- •Общий случай плоского движения
- •Основное свойство плоского движения.
- •Сравнительный характер поступательного и вращательного движения.
- •Колебательные движения
- •Смещение, скорость, ускорение, фаза, начальная фаза колебательного движения.
- •Энергия незатухающего колебательного движения Гармонический осциллятор
- •Сложение колебаний одного направления и биений
- •Сложение взаимно перпендикулярных колебаний. Фигура Лиссажу.
- •Математический маятник
- •Физический маятник(приведенная длина, точка качения и их св-ва, вывод формулы периода).
- •[Править]Вычисление
- •Затухающие колебания(логарифмический декремент, 4 подхода к определению добротности)
- •Вынужденные колебания
- •Консервативный гармонический осциллятор
- •II закон Ньютона к поступательному, вращательному, колебательному движению.
- •Теория относительности
- •Следствия из постулатов сто
- •1. Относительность одновременности событий
- •2. Относительность промежутков времени
- •3. Относительность расстояний
- •4. Сложение скоростей в сто
- •5. Закон Ньютона в релятивистской форме
- •6. Связь между энергией и массой
- •Молекулярная физика Адиабатический процесс
- •Физический смысл адиабатического процесса
- •Адиабата Пуассона
- •Политропный процесс
- •Теорема Больцмана
- •[Править]h-теорема
- •Молекулярная теплоемкость газа.
- •Теплоёмкость для различных состояний вещества
- •Термодинамика Первое начало термодинамики
- •[Править]Частные случаи
- •Работа газа при изопроцессах
- •Молярная и удельная теплоемкость газа.
- •II начало термодинамики
- •Ограничения
- •Обратимые и необратимые процессы
- •Квазистатический процесс Квазистатический процесс
- •Значение квазистатических процессов
- •Виды квазистатических процессов
- •Тепловые, холодильные машины.(их кпд) Цикл Карно.
- •Кпд тепловой машины Карно
- •Приведенная теплота и теорема Клаузиса
- •Энтропия
- •Изменение энтропии при квазистопическом процессе.
- •Энтропия в изолированной системе
- •Макро и микро состояния.
- •Термодинамическая вероятность состояний
- •Эргодическая гипотеза Статистическое толкование энтропии
- •Теорема Нерста
- •Параметрическая формула и распределение Больцмана
- •Распределение Максвелла Реальные газы
- •Уравнение Ван-дер-Ваальса
- •Уравнение состояния
- •Внутренняя энергия газа Ван-дер-Ваальса
- •Явление переноса
- •Эффективное сечение
- •Число столкновений и средняя длина свободного пробега молекул в газах
Приведенная теплота и теорема Клаузиса
Из рассмотренного цикла Карно (п. 5.4) видно, что равны между собой отношения теплот к температурам, при которых они были получены или отданы в изотермическом процессе:
|
|
|
|
Отношение
теплоты Q в изотермическом процессе к
температуре, при которой происходила
передача теплоты, называется приведенной
теплотой ![]() :
:
|
|
|
(6.1.1) |
Для
подсчета приведенной теплоты в
произвольном процессе необходимо
разбить этот процесс на бесконечно
малые участки, где Т можно
считать константой. Приведенная теплота
на таком участке будет равна ![]() Суммируя приведенную теплоту на всех
участках процесса, получим:
Суммируя приведенную теплоту на всех
участках процесса, получим:
|
|
|
|
Тогда в обратимом цикле Карно (п. 5.3, 5.4) имеем:
|
|
|
|
Этот результат справедлив для любого обратимого процесса. Таким образом, для процесса, происходящего по замкнутому циклу
|
|
|
(6.1.2) |
Из
равенства нулю интеграла, взятого по
замкнутому контуру, следует, что
подынтегральное выражение ![]() есть
полный дифференциал некоторой функции,
которая определяется только состоянием
системы и не зависит от пути, каким
система пришла в это состояние. Это
позволяет ввести новую функцию
состояния S:
есть
полный дифференциал некоторой функции,
которая определяется только состоянием
системы и не зависит от пути, каким
система пришла в это состояние. Это
позволяет ввести новую функцию
состояния S:
|
|
|
(6.1.3) |
Функция состояния, полный дифференциал которой равен , называется энтропией (от греч. entropia – поворот, превращение) – мера способности теплоты превращаться в другие виды энергии. Энтропия S – это отношение полученной или отданной теплоты к температуре, при которой происходил этот процесс. Понятие энтропии впервые введено Р. Клаузиусом в 1854 г.
Для обратимых процессов изменение энтропии, как следует из (6.1.2),
|
|
|
(6.1.4) |
Это выражение называется равенство Клаузиуса.
Энтропия
Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.
![]() ,
,
где dS — приращение энтропии; δQ — минимальная теплота, подведенная к системе; T — абсолютная температура процесса;
Из теоремы Клаузиуса следует, что приведенная теплота подобно энергии (потенциальной, внутренней) является функцией состояния (не зависит от пути перехода и зависит только от состояния системы). Независимость интеграла
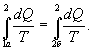
от пути перехода означает, что этот интеграл выражает собой изменение некоторой функции состояния системы, она называется энтропия и обозначается буквой S. Изменение энтропии системы, очевидно, равно
|
(9.30) |
Мы
говорим только об изменении энтропии
(подобно изменению потенциальной
энергии ![]() ,
для которой не важно где начало отсчета).
Из уравнения (9.30) вытекает основное
количественное выражение второго начала
термодинамики
,
для которой не важно где начало отсчета).
Из уравнения (9.30) вытекает основное
количественное выражение второго начала
термодинамики
|