Затухающие колебания(логарифмический декремент, 4 подхода к определению добротности)

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида   в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний   или её квадрата.

В акустике: затухание — уменьшение уровня сигнала до полной неслышимости.

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.

(7.17)

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ 

или

(7.18)

Перепишем это уравнение в следующем виде:

и обозначим:

где   представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

(7.19)

Будем искать решение уравнения (7.19) в виде где U - некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим 

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение   тогда С вещественным ω решением этого уравнения, как мы знаем, является функция 

Таким образом, в случае малого сопротивления среды   , решением уравнения (7.19) будет функция

(7.20)

График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину   называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину   обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда

откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

Определение добротности:

Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Общая формула для добротности любой колебательной системы:

,

где:

• f₀ — резонансная частота колебаний

• W — энергия, запасённая в колебательной системе

• P_d — рассеиваемая мощность.

Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах - на зеркалах.

Для последовательного Колебательного контура в RLC цепях, в котором все три элемента включены последовательно:

,

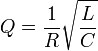где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.

Для параллельного контура, в котором индуктивность, емкость и сопротивление включены параллельно:

,

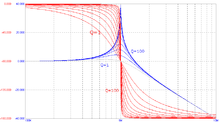
ЛАФЧХ колебательных звеньев с разной добротностью.

Для электрической цепи гораздо проще измерить амплитуду (ток или напряжение), чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды осцилляции, полоса на АЧХ будет   от пика (примерно −3 дБ, а 1/2 это −6 дБ). Поэтому чаще используется другое эквивалентное определение добротности, которое связывает ширину амплитудной резонансной кривой Δω по уровню  с круговой частотой резонанса ω₀ = 2πf₀:

,

где: δ - коэффициент затухания, равный полуширине резонансной кривой, N_e — число колебаний за время релаксации.

Логарифмический декремент затухания: