Напряженность и потенциал гравитационного поля.

Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела:

Если источником гравитационного поля является некое гравитирующее тело, то согласно закону всемирного тяготения:

 где:

• G — гравитационная постоянная;

• M_G — гравитационная масса тела-источника поля;

• R — расстояние от исследуемой точки пространства до центра масс тела-источника поля.

Применяя второй закон Ньютона и принцип эквивалентности гравитационной и инерционной масс:

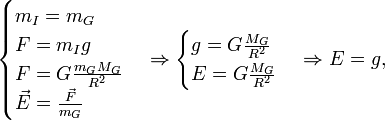
то есть напряжённость гравитационного поля численно (и по размерности) равна ускорению свободного падения в этом поле.

Гравитацио́нный потенциа́л — скалярная функция координат и времени, характеризующая гравитационное поле в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой  .

Гравитационный потенциал и уравнения движения

Движение частицы в гравитационном поле в классической механике определяется функцией Лагранжа, имеющей в инерциальной системе отсчета вид:

, где: m — масса частицы, q — координата частицы,   — потенциал гравитационного поля.

Подставляя выражение для лагранжиана L в уравнения Лагранжа:

,

получаем уравнения движения

.

Связь потенциальной энергии и силы

Пространство, в котором действуют консервативные силы, называется потенциальным полем.  Каждой точке потенциального поля соответствует некоторое значение силы   , действующей на тело, и некоторое значение потенциальной энергии  U. Значит, между силой     и  U  должна быть связь   , с другой стороны,  dA = –dU, следовательно   , отсюда

.

(5.3.6)

Проекции вектора силы на оси координат:

Вектор силы можно записать через проекции:

,  F = –grad U,

(5.3.7)

где   .  Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор     направлен в сторону наибыстрейшего уменьшения U.

Потенциальные кривые и энергетические уровни

Самый простой пример это вода в стакане.  Смотрим на него сбоку: это и есть потенциальная кривая.  Мы видим что уровень воды меньше чем стенки стакана. То есть вода находится как бы в потенциальной яме и не может вытечь.  А вот стенки стакана это есть потенциальный барьер, преодолев который вода выльется.  Единственное что, когда говорят о потенциальных величинах-- речь идет о запасе энергии.  В данном случае энергия будет E=mgh, mg постоянно в нашем случае(для капли вды к примеру) единственное что меняется это уровень(h). Думаю объяснил доходчиво)

Энергетический уровень — собственные значения энергии квантовых систем, то есть систем, состоящих из микрочастиц (электронов, протонов и других элементарных частиц) и подчиняющихся законам квантовой механики. Каждый уровень характеризуется определённым состоянием системы, или подмножеством таковых в случае вырождения. Понятие применимо к атомам (электронные уровни), молекулам (различные уровни, соответствующие колебаниям и вращениям), атомным ядрам (внутриядерные энергетические уровни) и т.д.