
- •Механика Кинематика криволинейного движения
- •Скорость и ускорение. Нормальное и тангенсальное.
- •Полное ускорение
- •Кривизна траектории.
- •Вращательное движение
- •Радиус вектор
- •Угловая скорость, ускорение
- •Зависимость угла скорости и угла поворота от времени.
- •Поступательное вращательное движение
- •Динамика Законы Ньютона
- •Сила как мера взаимодействия тел.
- •Поле Сил Силовые поля
- •Электростатическое поле (поле неподвижных зарядов)
- •Гравитационное поле
- •Электромагнитное поле, постоянное во времени (поле постоянных токов)
- •Электромагнитное поле (общий случай)
- •Границы применения сил, классификация Прямые и обратные задачи механики. Начальные и граничные условия.
- •Энергия и работа. (теорема о Ек)
- •Потенциальная энергия, как энергия в-я.
- •Системы изолированные и неизолированные.
- •Диссипация энергии в диссипативной системе
- •Работа переменной силы.
- •Работа и энергия в поле тяготения
- •Общие характеристики гравитационного поля.
- •Напряженность и потенциал гравитационного поля.
- •Гравитационный потенциал и уравнения движения
- •Связь потенциальной энергии и силы
- •Потенциальные кривые и энергетические уровни
- •Импульс (II закон Ньютона с использованием импульса).
- •Закон сохранения импульса
- •Вращательное движение
- •Момент силы.
- •Момент импульса.
- •Момент инерции
- •Осевые моменты инерции некоторых тел
- •Теорема Штейнера
- •[Править]Вывод
- •[Править]Пример
- •Основное уравнение динамики вращательного движения
- •Зако́н сохране́ния моме́нта
- •Гироскопический эффект
- •Кинетическая энергия вращающегося тела
- •Работа при вращательном движении
- •Общий случай плоского движения
- •Основное свойство плоского движения.
- •Сравнительный характер поступательного и вращательного движения.
- •Колебательные движения
- •Смещение, скорость, ускорение, фаза, начальная фаза колебательного движения.
- •Энергия незатухающего колебательного движения Гармонический осциллятор
- •Сложение колебаний одного направления и биений
- •Сложение взаимно перпендикулярных колебаний. Фигура Лиссажу.
- •Математический маятник
- •Физический маятник(приведенная длина, точка качения и их св-ва, вывод формулы периода).
- •[Править]Вычисление
- •Затухающие колебания(логарифмический декремент, 4 подхода к определению добротности)
- •Вынужденные колебания
- •Консервативный гармонический осциллятор
- •II закон Ньютона к поступательному, вращательному, колебательному движению.
- •Теория относительности
- •Следствия из постулатов сто
- •1. Относительность одновременности событий
- •2. Относительность промежутков времени
- •3. Относительность расстояний
- •4. Сложение скоростей в сто
- •5. Закон Ньютона в релятивистской форме
- •6. Связь между энергией и массой
- •Молекулярная физика Адиабатический процесс
- •Физический смысл адиабатического процесса
- •Адиабата Пуассона
- •Политропный процесс
- •Теорема Больцмана
- •[Править]h-теорема
- •Молекулярная теплоемкость газа.
- •Теплоёмкость для различных состояний вещества
- •Термодинамика Первое начало термодинамики
- •[Править]Частные случаи
- •Работа газа при изопроцессах
- •Молярная и удельная теплоемкость газа.
- •II начало термодинамики
- •Ограничения
- •Обратимые и необратимые процессы
- •Квазистатический процесс Квазистатический процесс
- •Значение квазистатических процессов
- •Виды квазистатических процессов
- •Тепловые, холодильные машины.(их кпд) Цикл Карно.
- •Кпд тепловой машины Карно
- •Приведенная теплота и теорема Клаузиса
- •Энтропия
- •Изменение энтропии при квазистопическом процессе.
- •Энтропия в изолированной системе
- •Макро и микро состояния.
- •Термодинамическая вероятность состояний
- •Эргодическая гипотеза Статистическое толкование энтропии
- •Теорема Нерста
- •Параметрическая формула и распределение Больцмана
- •Распределение Максвелла Реальные газы
- •Уравнение Ван-дер-Ваальса
- •Уравнение состояния
- •Внутренняя энергия газа Ван-дер-Ваальса
- •Явление переноса
- •Эффективное сечение
- •Число столкновений и средняя длина свободного пробега молекул в газах
Работа и энергия в поле тяготения
Определим
работу, которую совершают силы поля
тяготения при перемещении в поле
материальной точки массой m. Вычислим,
какую надо затратить работу для удаления
тела массой m от Земли. На расстоянии R
(рис. 1) на тело действует сила
![]()
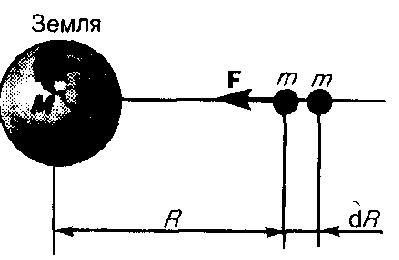
Рис.1
При
перемещении этого тела на расстояние
dR совершается работа
![]() (1)
Знак
минус появляется потому, что сила и
перемещение в данном случае противоположны
по направлению (рис. 1).
Если
тело перемещать с расстояния R1 до
R2,
то работа
(1)
Знак
минус появляется потому, что сила и
перемещение в данном случае противоположны
по направлению (рис. 1).
Если
тело перемещать с расстояния R1 до
R2,
то работа
![]() (2)
Из
формулы (2) следует, что затраченная
работа в поле тяготения не зависит от
траектории перемещения, а зависит лишь
от начального и конечного положения
тела, т. е. силы
тяготения действительно консервативны,
а поле тяготения является
потенциальным.
Работа,
совершаемая консервативными силами,
равна изменению потенциальной энергии
системы, взятому со знаком минус, т.
е.
(2)
Из
формулы (2) следует, что затраченная
работа в поле тяготения не зависит от
траектории перемещения, а зависит лишь
от начального и конечного положения
тела, т. е. силы
тяготения действительно консервативны,
а поле тяготения является
потенциальным.
Работа,
совершаемая консервативными силами,
равна изменению потенциальной энергии
системы, взятому со знаком минус, т.
е.
![]() Из
формулы (2) получаем
Из
формулы (2) получаем
![]() (3)
Так
как в формулы входит только разность
потенциальных энергий в двух состояниях,
то для удобства принимают потенциальную
энергию при R2→∞
равной нулю (P2=0).
Тогда (3) запишется в виде P1=
-GmM/R1.
Поскольку первую точку мы выбрали
произвольно, то
(3)
Так
как в формулы входит только разность
потенциальных энергий в двух состояниях,
то для удобства принимают потенциальную
энергию при R2→∞
равной нулю (P2=0).
Тогда (3) запишется в виде P1=
-GmM/R1.
Поскольку первую точку мы выбрали
произвольно, то
![]() Величина
Величина
![]() является
энергетической характеристикой поля
тяготения и называется потенциалом. Потенциал
поля тяготения φ
- скалярная величина, которая определяется
потенциальной энергией тела единичной
массы в данной точке поля или работой
по перемещению единичной массы из данной
точки поля в бесконечность. Таким
образом, потенциал поля тяготения,
создаваемого телом массой М,
равен
является
энергетической характеристикой поля
тяготения и называется потенциалом. Потенциал
поля тяготения φ
- скалярная величина, которая определяется
потенциальной энергией тела единичной
массы в данной точке поля или работой
по перемещению единичной массы из данной
точки поля в бесконечность. Таким
образом, потенциал поля тяготения,
создаваемого телом массой М,
равен
![]() (4)
где
R - расстояние от этого тела до
рассматриваемой точки.
Из
формулы (4) следует, что геометрическое
место точек с равными потенциалами
образует сферическую поверхность
(R=const). Такие поверхности, для которых
потенциал постоянен,
называются эквипотенциальными.
Исследуем
взаимосвязь между потенциалом φ поля
тяготения и его напряженностью g. Из
выражений (1) и (4) вытекает, что элементарная
работа dA, совершаемая силами поля при
малом перемещении тела массой m,
равна
(4)
где
R - расстояние от этого тела до
рассматриваемой точки.
Из
формулы (4) следует, что геометрическое
место точек с равными потенциалами
образует сферическую поверхность
(R=const). Такие поверхности, для которых
потенциал постоянен,
называются эквипотенциальными.
Исследуем
взаимосвязь между потенциалом φ поля
тяготения и его напряженностью g. Из
выражений (1) и (4) вытекает, что элементарная
работа dA, совершаемая силами поля при
малом перемещении тела массой m,
равна
![]() С
другой стороны, dA=Fdl (dl -
элементарное перемещение). Учитывая
(24.1), полу¬чаем, что dA=mgdl,
т. е. mgdl=
-mdφ, или
С
другой стороны, dA=Fdl (dl -
элементарное перемещение). Учитывая
(24.1), полу¬чаем, что dA=mgdl,
т. е. mgdl=
-mdφ, или
![]() Величина
dφ/dl характеризует
изменение потенциала на единицу длины
в направлении перемещения в поле
тяготения. Можно показать,
что
Величина
dφ/dl характеризует
изменение потенциала на единицу длины
в направлении перемещения в поле
тяготения. Можно показать,
что
![]() (5)
где
(5)
где ![]() -
градиент скаляра φ. Знак минус в формуле
(5) показывает, что вектор
напряженности g направлен
в сторону убывания потенциала.
В
качестве частного примера, исходя из
представлений теории тяготения,
рассмотрим потенциальную энергию тела,
находящегося на высоте h относительно
Земли:
-
градиент скаляра φ. Знак минус в формуле
(5) показывает, что вектор
напряженности g направлен
в сторону убывания потенциала.
В
качестве частного примера, исходя из
представлений теории тяготения,
рассмотрим потенциальную энергию тела,
находящегося на высоте h относительно
Земли:
![]() где
R0 -
радиус Земли. Так как
где
R0 -
радиус Земли. Так как
![]() и
и ![]() то,
учитывая условие h<<R0,
получаем
то,
учитывая условие h<<R0,
получаем
![]()
Общие характеристики гравитационного поля.
Гравитацио́нное по́ле, или по́ле тяготе́ния — физическое поле, через которое осуществляется гравитационное взаимодействие.
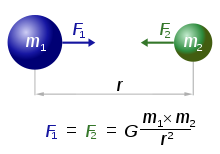
В рамках классической физики гравитационное взаимодействие описывается «законом всемирного тяготения» Ньютона, согласно которому сила гравитационного притяжения между двумя материальными точками с массами m1 и m2 пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними:
![]()
Здесь G — гравитационная
постоянная,
приблизительно равная ![]() м³/(кг
с²), R —
расстояние между точками.
м³/(кг
с²), R —
расстояние между точками.
Для расчёта поля в более сложных случаях, когда тяготеющие массы нельзя считать материальными точками, можно воспользоваться тем фактом, что поле ньютоновского тяготения потенциально. Если обозначить плотность вещества ρ, то потенциал поля φ удовлетворяет уравнению Пуассона:
Δφ = − 4πGρ
