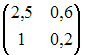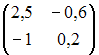Тест №6

  ЗАДАНИЕ N 1 сообщить об ошибке Тема: Поверхности второго порядка Даны уравнения поверхностей второго порядка: А)  B)  C)  D)  Тогда однополостный гиперболоид задается уравнением …

			D
			A
			C
			B

Решение: Так как каноническое уравнение однополостного гиперболоида имеет вид  , то искомое уравнение может иметь вид:  .

  ЗАДАНИЕ N 2 сообщить об ошибке Тема: Прямая на плоскости Угловой коэффициент прямой, заданной уравнением  , равен …

Решение: Выразим из уравнения   переменную  , а именно  . Тогда угловой коэффициент  .

 ЗАДАНИЕ N 3 сообщить об ошибке Тема: Прямая и плоскость в пространстве Даны точки   и  . Тогда уравнение плоскости, проходящей через точку   перпендикулярно вектору  , имеет вид …

  ЗАДАНИЕ N 4 сообщить об ошибке Тема: Полярные координаты на плоскости Точка   задана в полярной системе координат. Тогда ее прямоугольные координаты равны …

			,
			,
			,
			,

Решение: Прямоугольные координаты точки определяются формулами:  , то есть  .

 ЗАДАНИЕ N 5 сообщить об ошибке Тема: Вычисление определителей Корень уравнения   равен …

			– 1
			1
			4
			– 4

 ЗАДАНИЕ N 6 сообщить об ошибке Тема: Умножение матриц Произведение матрицы   размерностью 1×3 на матрицу   существует, если размерность матрицы   равна …

			31
			43
			23
			12

  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Линейные операции над матрицами Дана матрица   Если   где   – единичная матрица того же размера, что и матрица  , то матрица   равна …

Решение: При умножении матрицы на число каждый элемент матрицы умножается на данное число. При сложении или вычитании матриц одинаковой размерности соответствующие элементы матриц складываются или вычитаются друг из друга. Тогда:

  ЗАДАНИЕ N 8 сообщить об ошибке Тема: Системы линейных уравнений Решение системы   может иметь вид …

Решение: По методу Гаусса приведем матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем расширенную матрицу системы и преобразуем ее:    . Следовательно, система может быть записана в виде уравнения:  , где   – свободная переменная, а   – базисная. Общее решение будет иметь вид:  . Значит решением данной системы может быть  (2С;  С).

 ЗАДАНИЕ N 9 сообщить об ошибке Тема: Обратная матрица Дана матрица 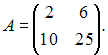  Тогда обратная матрица   имеет вид …

  ЗАДАНИЕ N 10 сообщить об ошибке Тема: Ранг матрицы Ранг матрицы   равен двум, если …

			минор второго порядка не равен нулю
			значения   и   равны нулю
			все миноры первого порядка равны нулю
			определитель матрицы равен двум

Решение: Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю.